
Concept explainers
For the problem specified in the table, build upon the results of the original problem to determine the minimum factor of safety for yielding. Use both the maximum-shear-stress theory and the distortion-energy theory, and compare the results. The material is 1018 CD steel.


3–79* Repeat Prob. 3–77 with T = 900 lbf · in, a = 6 in, b = 5 in, c = 10 in, d = 1.375 in, e = 4 in, f = 10 in, and g = 6 in.
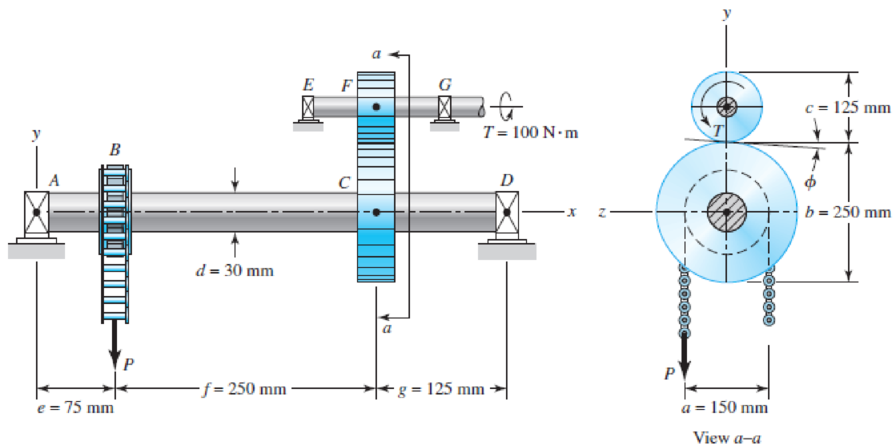
3–77* A torque T = 100 N · m is applied to the shaft EFG, which is running at constant speed and contains gear F. Gear F transmits torque to shaft ABCD through gear C, which drives the chain sprocket at B, transmitting a force P as shown. Sprocket B, gear C, and gear F have pitch diameters of a = 150, b = 250, and c = 125 mm, respectively. The contact force between the gears is transmitted through the pressure angle ϕ = 20°. Assuming no frictional losses and considering the bearings at A, D, E, and G to be simple supports, locate the point on shaft ABCD that contains the maximum tensile bending and maximum torsional shear stresses. Combine these stresses and determine the maximum principal normal and shear stresses in the shaft.
Want to see the full answer?
Check out a sample textbook solution
Chapter 5 Solutions
Shigley's Mechanical Engineering Design (McGraw-Hill Series in Mechanical Engineering)
- Two sections of steel drill pipe, joined by bolted flange plates at Ä are being tested to assess the adequacy of both the pipes. In the test, the pipe structure is fixed at A, a concentrated torque of 500 kN - m is applied at x = 0.5 m, and uniformly distributed torque intensity t1= 250 kN m/m is applied on pipe BC. Both pipes have the same inner diameter = 200 mm. Pipe AB has thickness tAB=15 mm, while pipe BC has thickness TBC= 12 mm. Find the maximum shear stress and maximum twist of the pipe and their locations along the pipe. Assume G = 75 GPa.arrow_forwardSolve the preceding problem if the thickness of the steel plate is. t = 12 mm. the gage readings are x = 530 × 10-6 (elongation) and y = -210 -× l0-6 (shortening), the modulus is E = 200 GPa, and Poisson’s ratio is v = 0.30.arrow_forwardThe strength-to-weight ratio of a structural material is defined as its load-carrying capacity divided by its weight. For materials in tension, use a characteristic tensile stress obtained from a stress-strain curve as a measure of strength. For instance, either the yield stress or the ultimate stress could be used, depending upon the particular application. Thus, the strength-to-weight ratio RS/Wfor a material in tension is defined as Rs/w= in which a is the characteristic stress and 7 is the weight density. Note that the ratio has units of length. Using the ultimate stress Uas the strength parameter, calculate the strength-to-weight ratio (in units of meters) for each of the following materials: aluminum alloy 606I-T6, Douglas fir (in bending}, nylon. structural steel ASTM-A57.2, and a titanium alloy. Obtain the material properties from Tables [-1 and 1-3 of Appendix I. When a range of values is given in a table, use the average value.arrow_forward
- Q1: A ductile bar of aluminum 1010 alloy. Using the distortion-energy and maximum- shear-stress theories determine the factors of safety for the following plane stress states: (α) σχ = 180 MPa, σy = 100 MPa (b) σx = 180 MPa, Txy = (c) σx = -160 MPa, Txy = 150 MPa (d) Txy 100 MPa = 100 MPaarrow_forwardDo not give answer in image and hand writingarrow_forwardplease i want a clear solutionarrow_forward
- Sy=370 MPaarrow_forwardA steel plate is subjected to a constant amplitude uniaxial fatigue loads to produce stresses, max = 180 MPa and min = -40 MPa. The static properties of the steel are YS= 500 MPa, UTS= 600 MPa, E= 207 GPa and Kc= 100 MPa-m1/2 . If the plate contains an initial through the thickness edge crack of 0.5 mm how many fatigue cycles will be required to break the plate. Please state any assumptions you make.arrow_forwardBar of steel, (yield strenght Sy = 469 MPa) is subjected to the following stresses; σx = 218 MPa , σy = -158 MPa , τxy = 138 MPa Using the Distortion-Energy Theory determine the factor of safety and check is the bar will fail or not.arrow_forward
- Consider a machine element as shown in the figure. The stress element at a critical point on this element is shown. Determine the smallest yield stress for a steel that can be selected for the member, based on the maximum-shear-stress theory. What result you expect if maximum distortion energy theory is used. 80ksi 25 ksiarrow_forward1. We can visualize the factor of safety for an arbitrary stress using a surface in principal stress space. For a ductile material that yields according to a von Mises criterion with a yield stress σy, sketch the von Mises surface in σ₁ - 02 space and sketch the stress surface that corresponds to a factor of safety FoS = 2. For a brittle material that yields according to a max normal (Rankine) criterion with a tensile strength Gyt and a compressive strength σvc = 20yt, sketch the yield surface and the surface that corresponds to a factor of safety FoS = 2.arrow_forwardThe plate of the figure is subjected to a bending moment with irregular cycles, which are repeated. In the graphic one of this cycles is represented in terms of stress which appears in each section whose height is h. The piece is made of ductile steel. Determine the number of repetitions of the sequence which the piece can resist before the failure takes place due to fatigue considering a reliability of 95 %. Data: Sult = 1.000 MPa Syp 3D800 Mра thickness e = 4 mm H = 10 cm h = 5 cm r=1 cm ka = 0,72 kp = 0,95 S(MPa) M 400 h 300 200 100 W -100 -200arrow_forward
 Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning
Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning
