Chapter 5, Problem 41P

5-39* to 5-55* For the problem specified in the table, build upon the results of the original problem to determine the minimum factor of safety for yielding. Use both the maximum-shear-stress theory and the distortion-energy theory, and compare the results. The material is 1018 CD steel.

Problem Number	Original Problem, Page Number
5-41*	3-70, 151

3-68* to 3-71* A countershaft two V-belt pulleys is shown in the figure. Pulley A receives power from a motor through a belt with the belt tensions shown. The power is transmitted through the shaft and delivered to the belt on pulley B. Assume the belt tension on the loose side at B is 15 percent of the tension on the tight side.

1. (a)   Determine the tensions in the belt on pulley B, assuming the shaft is running at a constant speed.
2. (b)   Find the magnitudes of the bearing reaction forces, assuming the bearings act as simple supports.
3. (c)   Draw shear-force and bending-moment diagrams for the shaft. If needed, make one set for the horizontal plane and another set for the vertical plane.
4. (d)   At the point of maximum bending moment, determine the bending stress and the torsional shear stress.
5. (e)   At the point of maximum bending moment, determine the principal stresses and the maximum shear stress.

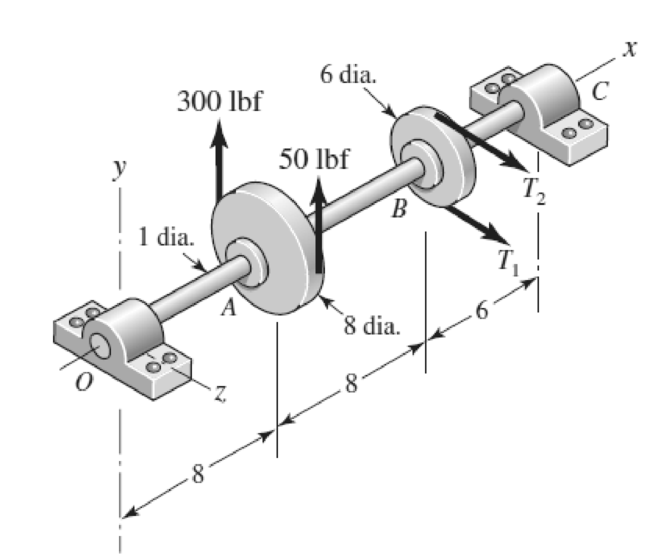
Problem 3-70*

Dimensions in inches.

To determine

The factor of safety for yielding from maximum-shear-stress theory.

The factor of safety for yielding from distortion-energy theory.

Answer to Problem 41P

The factor of safety for yielding from maximum-shear-stress theory is $2.27$.

The factor of safety for yielding from distortion-energy theory is $2.33$.

Explanation of Solution

The Free body diagram of pulley $A$ is shown below.

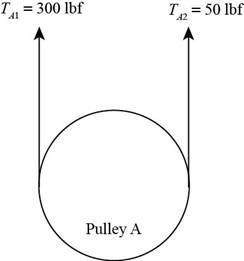
Figure (1)

The free body diagram of pulley $B$ is shown below.

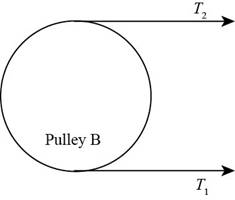
Figure (2)

The tension loose side is $T_2$ and the tension on the tight side is $T_1$.

It is given that the belt tension on the loose side at $B$ is $15\%$ of the tension on the tight side.

Write the relationship between tension on the loose side with respect to tension on the tight side.

$T_2=0.15T_1$ (I)

Here, the tension on the tight side is $T_1$ and the tension on the loose side is $T_2$.

Write the equation to balance the tension on the counter shaft.

$\begin{array}{c}{\displaystyle \sum T}=0\\ \left(T_{A1}-T_{A2}\right)\frac{d_A}{2}-\left(T_1-T_2\right)\frac{d_B}{2}=0\end{array}$ (II)

Here, the tension on the tight side of pulley $A$ is $T_{A1}$, the tension on the loose side of pulley $A$ is $T_{A2}$, diameter of shaft $A$ is $d_A$ and the diameter of shaft $B$ is $d_B$.

Substitute $0.15T_1$ for $T_2$ in Equation (II).

Calculate the tension on the loose side.

$\begin{array}{c}\left(T_{A1}-T_{A2}\right)\frac{d_A}{2}-\left(T_1-0.15T_1\right)\frac{d_B}{2}=0\\ T_1=\frac{1}{0.85}\left(\left(T_{A1}-T_{A2}\right)\frac{d_A}{d_B}\right)\end{array}$ (III)

Write the magnitude of bearing reaction force at $C$ in $z$ direction.

$\begin{array}{c}{\displaystyle \sum M_{Oy}}=0\\ -\left(T_1+T_2\right)\left(l_{OA}+l_{AB}\right)-R_{Cz}\left(l_{OA}+l_{AB}+l_{BC}\right)=0\\ R_{Cz}=\frac{-\left(T_1+T_2\right)\left(l_{OA}+l_{AB}\right)}{\left(l_{OA}+l_{AB}+l_{BC}\right)}\end{array}$ (IV)

Here, the magnitude of the bearing force at $C$ in $z$ direction is $R_{Cz}$, distance between $O$ and $A$ is $l_{OA}$, distance between $A$ and $B$ is $l_{AB}$ and distance between $B$ and $C$ is $l_{BC}$.

Write the magnitude of bearing reaction force at $O$ in $z$ direction.

$\begin{array}{c}{\displaystyle \sum F_z}=0\\ R_{Oz}+\left(T_1+T_2\right)+R_{Cz}=0\\ R_{Oz}=-\left(T_2+T_1\right)-R_{Cz}\end{array}$ (V)

Write the magnitude of bearing reaction force at $C$ in $y$ direction.

$\begin{array}{c}{\displaystyle \sum M_{Oz}}=0\\ R_{Cy}\left(l_{OA}+l_{AB}+l_{BC}\right)+\left(T_{A1}+T_{A2}\right)l_{OA}=0\\ R_{Cy}=-\frac{\left(T_{A1}+T_{A2}\right)l_{OA}}{\left(l_{OA}+l_{AB}+l_{BC}\right)}\end{array}$ (VI)

Here, the magnitude of bearing force at $C$ in $y$ direction is $R_{Cy}$.

Write the magnitude of bearing force at $O$ in $y$ direction.

$\begin{array}{c}{\displaystyle \sum F_y}=0\\ R_{Oy}+\left(T_{A1}+T_{A2}\right)+R_{Oz}=0\\ R_{Oy}=-\left(T_{A1}+T_{A2}\right)-R_{Cz}\end{array}$ (VII)

Here, the magnitude of bearing reaction force at $O$ in $z$ direction is $R_{Oz}$.

Calculate the bearing reaction force at $B$.

$R_C=\sqrt{R_{Cy}^2+R_{Cz}^2}$ (VIII)

Here, the bearing reaction force at $C$ is $R_C$.

Calculate the bearing reaction force at $O$.

$R_O=\sqrt{R_{Oy}^2+R_{Oz}^2}$ (IX)

Here, the bearing reaction force at $O$ is $R_O$.

The calculations for shear force and bending moment diagram in $y\text{-}$ direction.

Calculate the shear force at $O$ in $y$ direction.

$S{F}_{Oy}=R_{Oy}$ (X)

Here, the shear force at $O$ in $y$ direction is $S{F}_{Oy}$.

Calculate the shear force at $A$ in $y$ direction.

$S{F}_{Ay}=S{F}_{Oy}+(T_{A1}+T_{A2})$ (XI)

Here, the shear force at $A$ in $y$ direction is $S{F}_{Ay}$.

Calculate the shear force at $C$ in $y\text{-}$ direction.

$S{F}_{Cy}=S{F}_{Ay}+R_{Cy}$ (XII)

Here, the shear force at $C$ in $y$ direction is $S{F}_{Cy}$.

Calculate the moment at $O$ and $C$.

$M_O=M_C=0$ (XIII)

The moment at the supports of the simply supported beam is zero.

Calculate the moment at $A$ in $y$ direction.

$M_{Ay}=S{F}_{Oy}\times l_{OA}$ (XIV)

Here, the moment at $A$ is $M_A$ in $y$ direction.

Calculate the moment at $B$ in $y$ direction.

$M_{By}=R_{Cy}\times l_{BC}$ (XV)

Here, the moment at $A$ is $M_{By}$ in $y$ direction.

The calculations for shear force and bending moment diagram in $z\text{-}$ direction.

Calculate the shear force at $O$ in $z$ direction.

$S{F}_{Oz}=-R_{Oz}$ (XVI)

Here, the shear force at $O$ in $z$ direction is $S{F}_{Oz}$.

Calculate the shear force at $B$ in $z$ direction.

$S{F}_{Bz}=S{F}_{Oz}-\left(T_1+T_2\right)$ (XVII)

Here, the shear force at $B$ in $z$ direction is $S{F}_{Bz}$.

Calculate the shear force at $C$ in $z$ direction.

$S{F}_{Cz}=S{F}_{Bz}-R_{Cz}$ (XVIII)

Here, the shear force at $C$ in $z$ direction is $S{F}_{Cz}$.

Calculate the moment at $O$ and $C$.

$M_O=M_C=0$ (XIX)

The moment at the supports of the simply supported beam is zero.

Calculate the moment at $A$ in $z$ direction.

$M_{Az}=S{F}_{Oz}\times l_{OA}$ (XX)

Here, the moment at $A$ is $M_{Az}$ in $z$ direction.

Calculate the moment at $B$ in $z$ direction.

$M_{Bz}=-R_{Cz}\times l_{BC}$ (XXI)

Write the net moment at $A$.

$M_A=\sqrt{M_{Ay}^2+M_{Az}^2}$ (XXII)

Here, the net moment at $A$ is $M_A$.

Write the net moment at $B$.

$M_B=\sqrt{M_{By}^2+M_{Bz}^2}$ (XXIII)

Here, the net moment at $B$ is $M_B$.

Write the torque transmitted by shaft from $A$ to $B$.

$T=\left(T_{A1}-T_{A2}\right)\times \frac{d_A}{2}$ . (XXIV)

Here, the torque transmitted by shaft from $A$ to $B$ is $T$.

Calculate the bending stress.

$\sigma =\frac{32M_B}{\pi d^3}$ (XXV)

Here, the bending stress is $\sigma$ and diameter of shaft is $d$.

Calculate the shear stress.

$\tau =\frac{16T}{\pi d^3}$ (XXVI)

Here, the shear stress is $\tau$.

Calculate the maximum principal stress.

${\sigma }_1=\frac{\sigma }{2}+\sqrt{{\left(\frac{\sigma }{2}\right)}^2+{\tau }^2}$ (XXVII)

Here, the maximum principal stress is ${\sigma }_1$.

Calculate the minimum principal stress.

${\sigma }_2=\frac{\sigma }{2}-\sqrt{{\left(\frac{\sigma }{2}\right)}^2+{\tau }^2}$ (XXVIII)

Here, the minimum principal stress is ${\sigma }_2$.

Calculate the maximum shear stress.

${\tau }_{\max }=\sqrt{{\left(\frac{\sigma }{2}\right)}^2+{\tau }^2}$ (XXIX)

Here, maximum shear stress is ${\tau }_{\max }$.

Calculate the factor of safety from maximum-shear-stress theory.

$n=\frac{S_y}{{\sigma }_1-{\sigma }_2}$ (XXX)

Here, the maximum yield stress for $1018$ CD steel is $S_y$.

Calculate the factor of safety from distortion-energy theory.

$n=\frac{S_y}{{\sigma }^{\prime }}$ (XXXI)

Here, the Von Mises stress is ${\sigma }^{\prime }$.

Write the expression for von Mises stress.

$\sigma \text{'}={\left({\sigma }_1^2-{\sigma }_1.{\sigma }_2+{\sigma }_2^2\right)}^{\frac{1}{2}}$

Substitute $\left[{\left({\sigma }_1^2-{\sigma }_1.{\sigma }_2+{\sigma }_2^2\right)}^{\frac{1}{2}}\right]$ for $\sigma \text{'}$ in the Equation (XXXI).

$n=\frac{S_y}{\left[{\left({\sigma }_1^2-{\sigma }_1.{\sigma }_2+{\sigma }_2^2\right)}^{\frac{1}{2}}\right]}$ (XXXII)

Conclusion:

Substitute $300\text{lbf}$ for $T_{A1}$, $50\text{lbf}$ for $T_{A2}$, $8\text{in}$ for $d_A$ and $6\text{in}$ for $d_B$  in Equation (III).

$\begin{array}{c}{T}_1=\frac{1}{0.85}\left(\left(300\text{lbf}-50\text{lbf}\right)\times \frac{8\text{}\text{ in}}{6\text{ in}}\right)\\ =392.16\text{lbf}\end{array}$

Substitute $392.16\text{lbf}$ for $T_2$ in Equation (I)

$\begin{array}{c}{T}_2=0.15\times 392.16\text{lbf}\\ =58.82\text{lbf}\end{array}$

Substitute $392.16\text{lbf}$ for $T_1$, $58.82\text{lbf}$ for $T_2$, $8\text{in}$ for $l_{OA}$, $8\text{in}$ for $l_{AB}$ and $6\text{in}$ for $l_{BC}$ Equation (IV).

$\begin{array}{c}{R}_{Cz}=\frac{\left[\left(-(392.16\text{lbf}+58.82\text{lbf})\left(8\text{in}+8\text{in}\right)\right)+\left((60\text{lbf}+40\text{lbf})\left(18\text{in}+10\text{in}\right)\right)\right]}{\left(8\text{in}+8\text{in}+6\text{in}\right)}\\ =-327.99\text{lbf}\end{array}$

Substitute $392.16\text{lbf}$ for $T_1$, $58.82\text{lbf}$ for $T_2$ and $-327.99\text{lbf}$ for $R_{Cz}$ in Equation (V).

$\begin{array}{c}{R}_{Oz}=-\left(58.82\text{lbf}+392.16\text{lbf}\right)+327.99\text{lbf}\\ =-122.99\text{lbf}\end{array}$

Substitute $300\text{lbf}$ for $T_{A1}$, $50\text{lbf}$ for $T_{A2}$, $8\text{in}$ for $l_{OA}$, $8\text{in}$ for $l_{AB}$ and $6\text{in}$ for $l_{BC}$ in Equation (VI.)

$\begin{array}{c}{R}_{Cy}=-\frac{\left(300\text{lbf}+50\text{lbf}\right)8\text{in}}{\left(8\text{in}+8\text{in}+6\text{in}\right)}\\ =\frac{\left(300\text{lbf}+50\text{lbf}\right)8\text{in}}{\left(22\text{in}\right)}\\ =-127.27\text{lbf}\end{array}$

Substitute $300\text{lbf}$ for $T_{A1}$, $50\text{lbf}$ for $T_{A2}$ and $-127.27\text{lbf}$ for $R_{Cz}$ in Equation (VII)

$\begin{array}{c}{R}_{Oy}=-\left(300\text{lbf}+50\text{lbf}\right)-127.27\text{lbf}\\ =-222.73\text{lbf}\end{array}$

Substitute $-327.99\text{N}$ for $R_{Cz}$ and $-127.27\text{lbf}$ for $R_{Cy}$ in Equation (VIII)

$\begin{array}{c}{R}_C=\sqrt{{\left(327.99\text{lbf}\right)}^2+{\left(127.27\text{lbf}\right)}^2}\\ =351.8\text{lbf}\end{array}$

Substitute $-222.73\text{lbf}$ for $R_{Oy}$ and $-122.99\text{lbf}$ for $R_{Oz}$ in Equation (IX).

$\begin{array}{c}{R}_O=\sqrt{{\left(222.73\text{lbf}\right)}^2+{\left(122.99\text{lbf}\right)}^2}\\ =254.43\text{lbf}\end{array}$

Substitute $-222.73\text{lbf}$ for $R_{Oy}$ in Equation (X).

$S{F}_{Oy}=-222.73\text{lbf}$

Substitute $-222.73\text{lbf}$ for $S{F}_{Oy}$, $300\text{lbf}$ for $T_{A1}$ and $50\text{lbf}$ for $R_{A2}$ in Equation (XI).

$\begin{array}{c}S{F}_{Ay}=-222.73\text{lbf}+(300\text{lbf}+50\text{lbf})\\ =127.27\text{lbf}\end{array}$

Substitute $-127.27\text{lbf}$ for $R_{Cy}$ and $127.27\text{lbf}$ for $S{F}_A$ in Equation (XII).

$\begin{array}{c}S{F}_{Cy}=127.27\text{lbf}-127.27\text{lbf}\\ =0\text{lbf}\end{array}$

Substitute $-222.73\text{lbf}$ for $S{F}_{Oy}$ and $8\text{in}$ for $l_{OA}$ in Equation (XIV).

$\begin{array}{c}{M}_{Ay}=-222.73\text{lbf}\times 8\text{in}\\ =-1781.84\text{lbf}\cdot \text{in}\end{array}$

Substitute $-127.27\text{lbf}$ for $R_O$ and $6\text{in}$ for $l_{BC}$ in Equation (XV).

$\begin{array}{c}{M}_{By}=-127.27\text{lbf}\times 6\text{in}\\ =-763.65\text{lbf}\cdot \text{in}\end{array}$

Thus, the shear force diagram and bending moment diagram for the shaft in $y\text{-}$ direction is as follows.

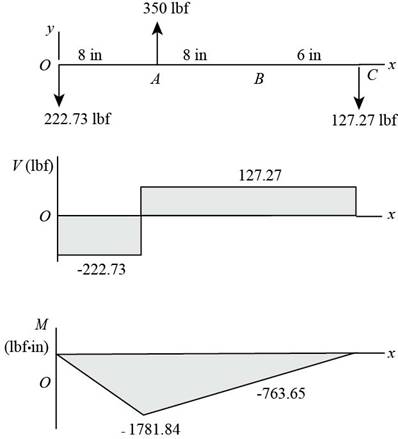
Figure (4)

Substitute $-122.99\text{lbf}$ for $R_{Oz}$ in Equation (XVI).

$S{F}_{Oz}=122.99\text{lbf}$

Substitute $122.99\text{lbf}$ for $S{F}_{Oz}$, $392.16\text{lbf}$ for $T_1$ and $58.82\text{lbf}$ for $T_2$ in Equation (XVII).

$\begin{array}{c}S{F}_{Bz}=122.99\text{lbf}-\left(392.16\text{lbf}+58.82\text{lbf}\right)\\ =-327.99\text{lbf}\end{array}$

Substitute $-327.99\text{lbf}$ for $S{F}_{Bz}$ and $-327.99\text{lbf}$ for $R_{Cz}$ in Equation (XVIII).

$\begin{array}{c}S{F}_{Cz}=-327.99\text{lbf}+327.99\text{lbf}\\ =0\text{lbf}\end{array}$

Substitute $122.99\text{lbf}$ for $S{F}_{Oy}$ and $8\text{in}$ for $l_{OA}$ in Equation (XX).

$\begin{array}{c}{M}_{Az}=122.99\text{lbf}\times 8\text{in}\\ =983.92\text{lbf}\cdot \text{in}\end{array}$

Substitute $-327.99\text{lbf}$ for $R_O$ and $6\text{in}$ for $l_{BC}$ in Equation (XXI).

$\begin{array}{c}{M}_{Bz}=-\left(-327.99\text{lbf}\right)\times 6\text{in}\\ =1967.84\text{lbf}\cdot \text{in}\end{array}$

Thus, the shear force diagram and bending moment diagram for the shaft in $y\text{-}$ direction is as follows.

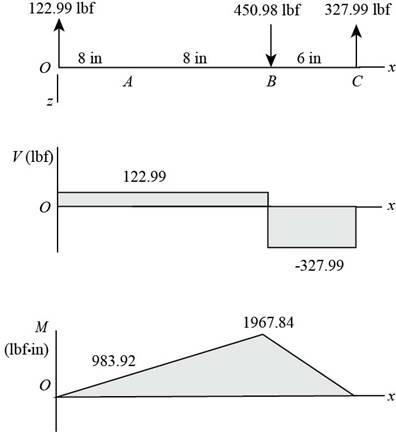
Figure (5)

Substitute $983.92\text{lbf}\cdot \text{in}$ for $M_{Az}$ and $-1781.84\text{lbf}\cdot \text{in}$ for $M_{Ay}$ in Equation (XXII).

$\begin{array}{c}{M}_A=\sqrt{{\left(983.92\text{lbf}\cdot \text{in}\right)}^2+{\left(-1781.84\text{lbf}\cdot \text{in}\right)}^2}\\ =2035\text{lbf}\cdot \text{in}\end{array}$

Substitute $1967.84\text{lbf}\cdot \text{in}$ for $M_{Bz}$ and $-763.65\text{lbf}\cdot \text{in}$ for $M_{By}$ in Equation (XXIII)

$\begin{array}{c}{M}_B=\sqrt{{\left(1967.84\text{lbf}\cdot \text{in}\right)}^2+{\left(-763.65\text{lbf}\cdot \text{in}\right)}^2}\\ =2111\text{lbf}\cdot \text{in}\end{array}$

Since, $M_B>M_A$, so the point of maximum bending stress is critically located at $B$.

Substitute $300\text{lbf}$ for $T_{A1}$, $50\text{lbf}$ for $T_{A2}$ and $8\text{in}$ for $d_A$ in Equation (XXIV).

$\begin{array}{c}T=\left(300\text{lbf}-50\text{lbf}\right)\frac{8\text{in}}{2}\\ =1000\text{lbf}\cdot \text{in}\end{array}$

Substitute $2111\text{lbf}\cdot \text{in}$ for $M_B$ and $1\text{in}$ for $d$ in Equation (XXV).

$\begin{array}{c}\sigma =\frac{32\times 2111\text{lbf}\cdot \text{in}}{\pi {\left(1\text{in}\right)}^3}\\ =21.5\text{kpsi}\end{array}$

Substitute $1000\text{lbf}\cdot \text{in}$ for $T$ and $1\text{in}$ for $d$ in Equation (XXVI).

$\begin{array}{c}\tau =\frac{16\times 1000\text{lbf}}{\pi {\left(1\text{in}\right)}^3}\\ =5.09\text{kpsi}\end{array}$

Substitute $21.5\text{kpsi}$ for $\sigma$ and $5.09\text{kpsi}$ for $\tau$ in Equation (XXVII).

$\begin{array}{c}{\sigma }_1=\frac{21.5\text{kpsi}}{2}+\sqrt{{\left(\frac{21.5\text{kpsi}}{2}\right)}^2+{\left(5.09\text{kpsi}\right)}^2}\\ =22.6\text{kpsi}\end{array}$

Substitute $21.5\text{kpsi}$ for $\sigma$ and $5.09\text{kpsi}$ for $\tau$ n Equation (XXVIII).

$\begin{array}{c}{\sigma }_2=\frac{21.5\text{kpsi}}{2}-\sqrt{{\left(\frac{21.5\text{kpsi}}{2}\right)}^2+5.09{\text{kpsi}}^2}\\ =-1.14\text{kpsi}\end{array}$

Substitute $21.5\text{kpsi}$ for $\sigma$ and $5.09\text{kpsi}$ for $\tau$ in Equation (XXIX).

$\begin{array}{c}{\tau }_{\max }=\sqrt{{\left(\frac{21.5\text{kpsi}}{2}\right)}^2+{\left(5.09\text{kpsi}\right)}^2}\\ =11.9\text{kpsi}\end{array}$

Refer to the Table A-20 “Deterministic ASTM Minimum Tensile and Yield Strengths for Some Hot-Rolled (HR) and Cold-Drawn (CD) Steels” and obtain $S_y=54\text{kpsi}$ for $1018$ CD steel.

Substitute $22.6\text{kpsi}$ for ${\sigma }_1$, $54\text{kpsi}$ for $S_y$ and $\left(-1.14\text{kpsi}\right)$ for ${\sigma }_2$ in the Equation (XXX).

$\begin{array}{c}n=\frac{54\text{kpsi}}{22.6\text{kpsi}-\left(-1.14\text{kpsi}\right)}\\ =2.274\\ \approx 2.27\end{array}$

Thus, the factor of safety for yielding from maximum-shear-stress theory is $2.27$.

Substitute $22.6\text{kpsi}$ for ${\sigma }_1$, $54\text{kpsi}$ for $S_y$ and $\left(-1.14\text{kpsi}\right)$ for ${\sigma }_2$ in the Equation (XXXII).

$\begin{array}{c}n=\frac{54\text{kpsi}}{{\left({\left(22.6\text{kpsi}\right)}^2-\left(22.6\text{kpsi}\right)\cdot \left(-1.14\text{kpsi}\right)+{\left(-1.14\text{kpsi}\right)}^2\right)}^{\frac{1}{2}}}\\ =2.328\\ \approx 2.33\end{array}$

Thus, the factor of safety for yielding from distortion-energy theory is $2.33$.