
Concept explainers
Consider the three connected objects shown in Figure P5.43. Assume first that the inclined plane is frictionless and that the system is in equilibrium. In terms of m, g, and θ, find (a) the mass M and (b) the tensions T1 and T2. Now assume that the value of M is double the value found in part (a). Find (c) the acceleration of each object and (d) the tensions T1 and T2. Next, assume that the coefficient of static friction between m and 2m and the inclined plane is μs and that the system is in equilibrium. Find (e) the maximum value of M and (f) the minimum value of M. (g) Compare the values of T2 when M has its minimum and maximum values.

Figure P5.43
(a)
The mass
Answer to Problem 43P
The mass
Explanation of Solution
The free body diagram of the mass
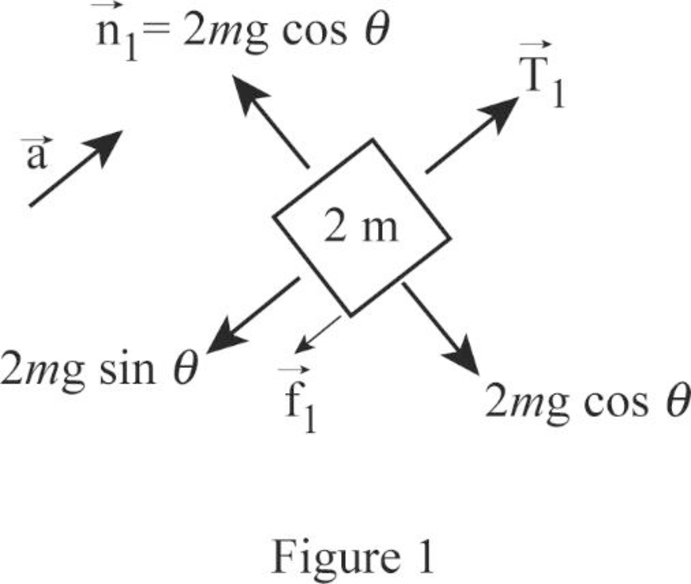
The free body diagram of the mass
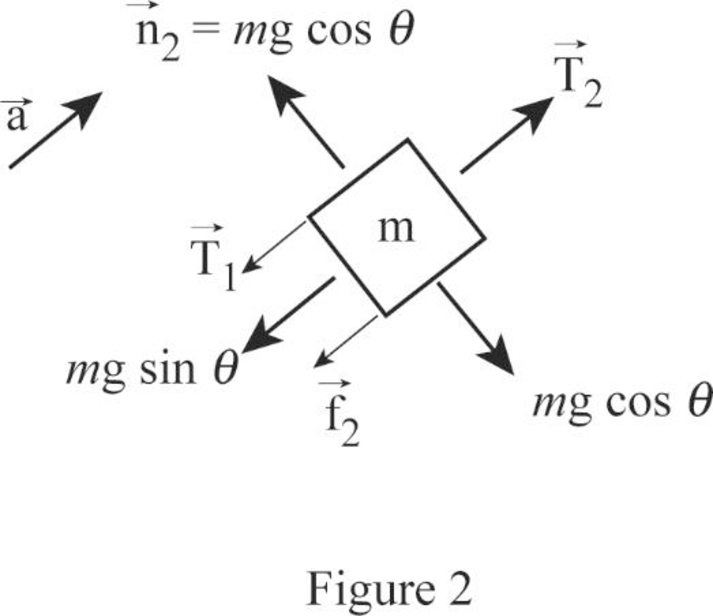
The free body diagram of the mass
Apply Newton’s second law in the Figure1.
Here,
Apply Newton’s second law in the Figure 2.
Here,
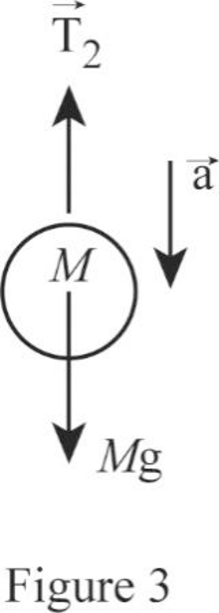
Apply Newton’s second law in the Figure 3.
Assume that, the system is in equilibrium,
Use equation (I) and (III), in (II).
Conclusion:
Therefore, the mass
(b)
The tensions
Answer to Problem 43P
The tension
Explanation of Solution
From the part (a),
Use equation (IV) in (III), and substitute
Conclusion:
Therefore, the tensions
(c)
The acceleration of each object when the value of
Answer to Problem 43P
The acceleration of each object when the value of
Explanation of Solution
Assume that,
Substitute,
Use equation (I) and (V) in (VII), substitute,
Conclusion:
Therefore, the acceleration of each object when the value of
(d)
The tensions
Answer to Problem 43P
The tensions
Explanation of Solution
Use equation (VI) in (I), substitute,
Use equation (VI) in (III), and use
Conclusion:
Therefore, the tensions
(e)
The maximum value of
Answer to Problem 43P
The maximum value of
Explanation of Solution
At the equilibrium the acceleration is zero, and the frictional forces acting down the incline.
Use
Use
Rewrite the equation (III) for
Use equation (IX) and (X) in (XI).
Conclusion:
Therefore, the maximum value of
(f)
The minimum value of
Answer to Problem 43P
The minimum value of
Explanation of Solution
Rewrite the equation (III) for
At the equilibrium the acceleration is zero, and impending motion up the incline, so the frictional forces acting up the incline.
Use
Since the frictional forces acting up the incline.
Use
Since the frictional forces acting up the incline.
Use equation (XII) and (XIII) in (XIV).
Conclusion:
Therefore, the minimum value of
(g)
The value of
Answer to Problem 43P
The value of
Explanation of Solution
Subtract equation (XII) from (XI).
Use
Conclusion:
Therefore, the value of
Want to see more full solutions like this?
Chapter 5 Solutions
Principles of Physics: A Calculus-Based Text
- 7. A race car accelerates from rest to 55 m s-1 in 5.0 seconds. The acceleration of the car Is m s-² 8. An object's speed increases uniformly from 10.5 km per hour to 99.8 km per hour in 2.41 seconds. Calculate the acceleration in m s-2 and express your answer to three significant figures. 9. The acceleration-time graph of a car is shown below. The initial speed of the car is 5.0 m s-1. # Acceleration (ms) 12 8.0- 4.0- 2.0 4.0 6.0 Time (s) Calculate the velocity of the car at t = 4.0 s. 3arrow_forwardNo chatgpt pls will upvotearrow_forwardNo chatgpt pls will upvotearrow_forward
- Problem Seven. A football receiver running straight downfield at 5.60 m/s is 11.5 m in front of the quarterback when a pass is thrown downfield at an angle of 35.0° horizon. above the 8.) If the receiver never changes speed and the ball is caught at the same height from which it was thrown, find the distance between the quarterback and the receiver when the catch is made. (A) 21.3 (B) 17.8 (C) 18.8 (D) 19.9 (E) 67.5arrow_forwardPlease solve and answer the question correctly please. Thank you!!arrow_forwardPlease solve and answer the question correctly please. Thank you!!arrow_forward
- Please view both photos, and answer the question correctly please. Thank you!!arrow_forwardA thrown brick hits a window, but doesn't break it. Instead it reverses direction and ends down on the ground below the window. Since the brick didn't break the glass, we know: О The force of the brick on the glass > the force of the glass on the brick. О The force of the brick on the glass the force of the glass on the brick. = О The force of the brick on the glass < the force of the glass on the brick. О The brick didn't slow down as it broke the glass.arrow_forwardAlexandra (wearing rubber boots for traction) is attempting to drag her 32.6-kg Golden Retriever across the smooth ice by applying a horizontal force. What force must she apply to move the dog with a constant speed of 0.950 m/s? ☐ 31.0 lb. ☐ 319 kg. ○ Zero. 32.6 kg.arrow_forward
- The figure shows a graph of the acceleration of an object as a function of the net force acting on it. The mass of this object, in grams, is closest to 11 a(m/s²) 8.0+ 6.0- 4.0- 2.0- 0+ F(N) 0.00 0.50 1.00 ☐ 130 ○ 8000 ☐ 89arrow_forwardValues that are within standard deviations represent measurements that are considered to be near the true value. Review the data from the lab and determine whether your data is within standard deviations. Report, using numerical values, whether your data for each angle is within standard deviations. An acceptable margin of error typically falls between 4% and 8% at the 95% confidence level. Review your data for each angle to determine whether the margin of error is within an acceptable range. Report with numerical values, whether your data for each angle is within an acceptable margin of error. Can you help explain what my data means in terms of the standard deviation and the ME? Thanks!arrow_forwardA sinusoidal wave is propagating along a stretched string that lies along the x-axis. The displacement of the string as a function of time is graphed in (Figure 1) for particles at x = 0 and at x = 0.0900 m. You are told that the two points x = 0 and x = 0.0900 m are within one wavelength of each other. If the wave is moving in the +x-direction, determine the wavelength. If instead the wave is moving in the -x-direction, determine the wavelength. Please show all stepsarrow_forward
 Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Physics for Scientists and Engineers, Technology ...PhysicsISBN:9781305116399Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers, Technology ...PhysicsISBN:9781305116399Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning
Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning Classical Dynamics of Particles and SystemsPhysicsISBN:9780534408961Author:Stephen T. Thornton, Jerry B. MarionPublisher:Cengage Learning
Classical Dynamics of Particles and SystemsPhysicsISBN:9780534408961Author:Stephen T. Thornton, Jerry B. MarionPublisher:Cengage Learning Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning





