Principles of Physics: A Calculus-Based Text
5th Edition
ISBN: 9781133104261
Author: Raymond A. Serway, John W. Jewett
Publisher: Cengage Learning
expand_more
expand_more
format_list_bulleted
Concept explainers
Videos
Textbook Question
Chapter 5, Problem 59P
A single bead can slide with negligible friction on a stiff wire that has been bent into a circular loop of radius 15.0 cm as shown in Figure P5.59. The circle is always in a vertical plane and rotates steadily about its vertical diameter with a period of 0.450 s. The position of the bead is described by the angle θ that the radial line, from the center of the loop to the bead, makes with the vertical. (a) At what angle up from the bottom of the circle can the bead stay motionless relative to the turning circle? (b) What If ? Repeat the problem, this time taking the period of the circle’s rotation as 0.850 s. (c) Describe how the solution to part (b) is different from the solution to part (a). (d) For any period or loop size, is there always an angle at which the bead can stand still relative to the loop? (e) Are there ever more than two angles? Arnold Arons suggested the idea for this problem.
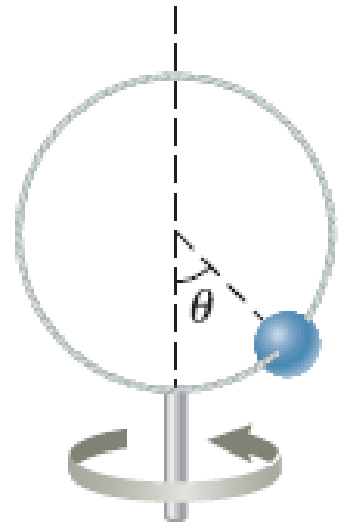
Figure P5.59
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
Need help on the following questions on biomechanics. (Please refer to images below)A gymnast weighing 68 kg attempts a handstand using only one arm. He plants his handat an angle resulting in the reaction force shown.A) Find the resultant force (acting on the Center of Mass)B) Find the resultant moment (acting on the Center of Mass)C) Draw the resultant force and moment about the center of mass on the figure below. Will the gymnast rotate, translate, or both? And in which direction?
Please help me on the following question (Please refer to image below)An Olympic lifter (m = 103kg) is holding a lift with a mass of 350 kg. The barexerts a purely vertical force that is equally distributed between both hands. Each arm has amass of 9 kg, are 0.8m long and form a 40° angle with the horizontal. The CoM for each armis 0.5 m from hand. Assuming the lifter is facing us in the diagram below, his right deltoidinserts 14cm from the shoulder at an angle of 13° counter-clockwise from the humerus.A) You are interested in calculating the force in the right deltoid. Draw a free body diagramof the right arm including the external forces, joint reaction forces, a coordinate system andstate your assumptions.B) Find the force exerted by the right deltoidC) Find the shoulder joint contact force. Report your answer using the magnitude and directionof the shoulder force vector.
I need help with part B. I cant seem to get the correct answer. Please walk me through what youre doing to get to the answer and what that could be
Chapter 5 Solutions
Principles of Physics: A Calculus-Based Text
Ch. 5.1 - You press your physics textbook flat against a...Ch. 5.1 - A crate is located in the center of a flatbed...Ch. 5.1 - You are playing with your daughter in the snow....Ch. 5.2 - You are riding on a Ferris wheel (Fig. 5.8) that...Ch. 5.3 - Which of the following is impossible for a car...Ch. 5.3 - A bead slides freely along a curved wire lying on...Ch. 5.4 - Consider a sky surfer falling through air, as in...Ch. 5 - The driver of a speeding empty truck slams on the...Ch. 5 - The manager of a department store is pushing...Ch. 5 - An object of mass m moves with acceleration a down...
Ch. 5 - An office door is given a sharp push and swings...Ch. 5 - Prob. 5OQCh. 5 - A pendulum consists of a small object called a bob...Ch. 5 - A door in a hospital has a pneumatic closer that...Ch. 5 - The driver of a speeding truck slams on the brakes...Ch. 5 - A child is practicing for a BMX race. His speed...Ch. 5 - A large crate of mass m is placed on the flatbed...Ch. 5 - Before takeoff on an airplane, an inquisitive...Ch. 5 - Prob. 12OQCh. 5 - As a raindrop falls through the atmosphere, its...Ch. 5 - An object of mass m is sliding with speed vi at...Ch. 5 - A car is moving forward slowly and is speeding up....Ch. 5 - Prob. 2CQCh. 5 - Prob. 3CQCh. 5 - Prob. 4CQCh. 5 - Prob. 5CQCh. 5 - Prob. 6CQCh. 5 - Prob. 7CQCh. 5 - Prob. 8CQCh. 5 - Prob. 9CQCh. 5 - Prob. 10CQCh. 5 - It has been suggested that rotating cylinders...Ch. 5 - Prob. 12CQCh. 5 - Why does a pilot tend to black out when pulling...Ch. 5 - Prob. 1PCh. 5 - Prob. 2PCh. 5 - Prob. 3PCh. 5 - Prob. 4PCh. 5 - Prob. 5PCh. 5 - The person in Figure P5.6 weighs 170 lb. As seen...Ch. 5 - A 9.00-kg hanging object is connected by a light,...Ch. 5 - Prob. 8PCh. 5 - A 3.00-kg block starts from rest at the top of a...Ch. 5 - Prob. 10PCh. 5 - Prob. 11PCh. 5 - A block of mass 3.00 kg is pushed up against a...Ch. 5 - Two blocks connected by a rope of negligible mass...Ch. 5 - Three objects are connected on a table as shown in...Ch. 5 - Why is the following situation impossible? Your...Ch. 5 - Prob. 16PCh. 5 - A light string can support a stationary hanging...Ch. 5 - Why is the following situation impossible? The...Ch. 5 - A crate of eggs is located in the middle of the...Ch. 5 - Prob. 20PCh. 5 - Prob. 21PCh. 5 - A roller coaster at the Six Flags Great America...Ch. 5 - Prob. 23PCh. 5 - Prob. 24PCh. 5 - Prob. 25PCh. 5 - A pail of water is rotated in a vertical circle of...Ch. 5 - Prob. 27PCh. 5 - A child of mass m swings in a swing supported by...Ch. 5 - Prob. 29PCh. 5 - (a) Estimate the terminal speed of a wooden sphere...Ch. 5 - Prob. 31PCh. 5 - Prob. 32PCh. 5 - Prob. 33PCh. 5 - A 9.00-kg object starting from rest falls through...Ch. 5 - Prob. 35PCh. 5 - Prob. 36PCh. 5 - Prob. 37PCh. 5 - Prob. 38PCh. 5 - Prob. 39PCh. 5 - Prob. 40PCh. 5 - Prob. 41PCh. 5 - Prob. 42PCh. 5 - Consider the three connected objects shown in...Ch. 5 - A car rounds a banked curve as discussed in...Ch. 5 - Prob. 45PCh. 5 - An aluminum block of mass m1 = 2.00 kg and a...Ch. 5 - Figure P5.47 shows a photo of a swing ride at an...Ch. 5 - Why is the following situation impossible? A...Ch. 5 - A space station, in the form of a wheel 120 m in...Ch. 5 - A 5.00-kg block is placed on top of a 10.0-kg...Ch. 5 - In Example 6.5, we investigated the forces a child...Ch. 5 - Prob. 52PCh. 5 - Prob. 53PCh. 5 - Prob. 54PCh. 5 - Prob. 55PCh. 5 - Prob. 56PCh. 5 - Prob. 57PCh. 5 - Why is the following situation impossible? A book...Ch. 5 - A single bead can slide with negligible friction...Ch. 5 - An amusement park ride consists of a large...Ch. 5 - Prob. 61PCh. 5 - Prob. 62PCh. 5 - Prob. 63PCh. 5 - If a single constant force acts on an object that...
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, physics and related others by exploring similar questions and additional content below.Similar questions
- Question 6: Chlorine is widely used to purify municipal water supplies and to treat swimming pool waters. Suppose that the volume of a particular sample of Cl₂ gas is 8.70 L at 895 torr and 24°C. (a) How many grams of Cl₂ are in the sample? ⚫ Atomic mass of CI = 35.453 g/mol • Molar mass of Cl₂ = 2 x 35.453 = 70.906 g/mol Solution: Use the Ideal Gas Law: Step 1: Convert Given Values • Pressure: P = 895 torr → atm PV= = nRT 1 P = 895 × = 1.1789 atm 760 • Temperature: Convert to Kelvin: T24273.15 = 297.15 K • Gas constant: R = 0.0821 L atm/mol. K Volume: V = 8.70 L Step 2: Solve for n . PV n = RT n = (1.1789)(8.70) (0.0821)(297.15) 10.25 n = = 0.420 mol 24.405 Step 3: Calculate Mass of Cl₂ Final Answer: 29.78 g of Cl₂. mass nx M mass= (0.420)(70.906) mass= 29.78 garrow_forwardE1 R₁ w 0.50 20 Ω 12 R₁₂ ww ΒΩ R₂ 60 E3 C RA w 15 Ω E2 0.25 E4 0.75 Ω 0.5 Ωarrow_forwardSolve plzarrow_forward
- how would i express force in vector form I keep getting a single numberarrow_forwardplease help me solve this questions. show all calculations and a good graph too :)arrow_forwardWhat is the force (in N) on the 2.0 μC charge placed at the center of the square shown below? (Express your answer in vector form.) 5.0 με 4.0 με 2.0 με + 1.0 m 1.0 m -40 με 2.0 μCarrow_forward
- What is the force (in N) on the 5.4 µC charge shown below? (Express your answer in vector form.) −3.1 µC5.4 µC9.2 µC6.4 µCarrow_forwardAn ideal gas in a sealed container starts out at a pressure of 8900 N/m2 and a volume of 5.7 m3. If the gas expands to a volume of 6.3 m3 while the pressure is held constant (still at 8900 N/m2), how much work is done by the gas? Give your answer as the number of Joules.arrow_forwardThe outside temperature is 25 °C. A heat engine operates in the environment (Tc = 25 °C) at 50% efficiency. How hot does it need to get the high temperature up to in Celsius?arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning
Physics for Scientists and Engineers, Technology ...PhysicsISBN:9781305116399Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Glencoe Physics: Principles and Problems, Student...PhysicsISBN:9780078807213Author:Paul W. ZitzewitzPublisher:Glencoe/McGraw-Hill
An Introduction to Physical SciencePhysicsISBN:9781305079137Author:James Shipman, Jerry D. Wilson, Charles A. Higgins, Omar TorresPublisher:Cengage Learning
Principles of Physics: A Calculus-Based Text
Physics
ISBN:9781133104261
Author:Raymond A. Serway, John W. Jewett
Publisher:Cengage Learning
Physics for Scientists and Engineers with Modern ...
Physics
ISBN:9781337553292
Author:Raymond A. Serway, John W. Jewett
Publisher:Cengage Learning
Physics for Scientists and Engineers: Foundations...
Physics
ISBN:9781133939146
Author:Katz, Debora M.
Publisher:Cengage Learning
Physics for Scientists and Engineers, Technology ...
Physics
ISBN:9781305116399
Author:Raymond A. Serway, John W. Jewett
Publisher:Cengage Learning
Glencoe Physics: Principles and Problems, Student...
Physics
ISBN:9780078807213
Author:Paul W. Zitzewitz
Publisher:Glencoe/McGraw-Hill
An Introduction to Physical Science
Physics
ISBN:9781305079137
Author:James Shipman, Jerry D. Wilson, Charles A. Higgins, Omar Torres
Publisher:Cengage Learning
What Is Circular Motion? | Physics in Motion; Author: GPB Education;https://www.youtube.com/watch?v=1cL6pHmbQ2c;License: Standard YouTube License, CC-BY