
Concept explainers
a.
To find the intervals on which the function is increasing by using analytical method.
a.
Answer to Problem 16RE
The function
Explanation of Solution
Given:
The function is
Calculation:
The function is increasing when
Below is the graph of
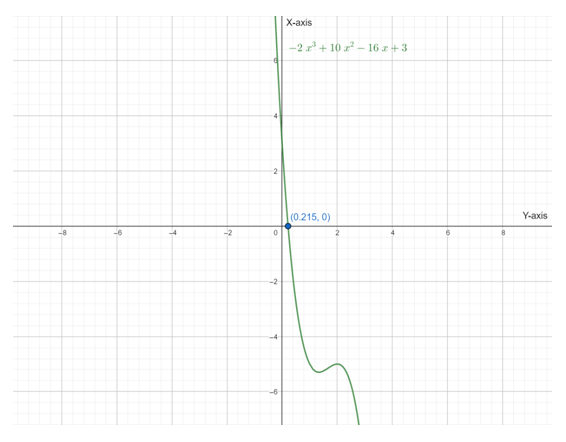
So , there are three intervals
Put
Function is increasing in interval
Put
Function is decreasing in interval
Put
Function is decreasing in interval
Below is the graph of
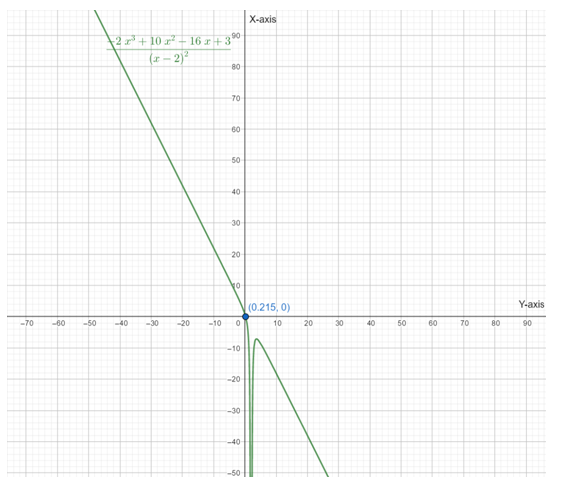
From graph also it is clear that the function
b.
To find the intervals on which the function is decreasing by using analytical method.
b.
Answer to Problem 16RE
The function
Explanation of Solution
Given:
The function is
Calculation:
The function is decreasing when
Below is the graph of
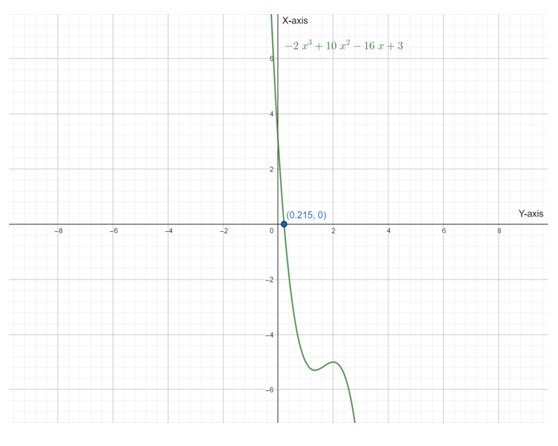
So , there are three intervals
Put
Function is increasing in interval
Put
Function is decreasing in interval
Put
Function is decreasing in interval
Below is the graph of
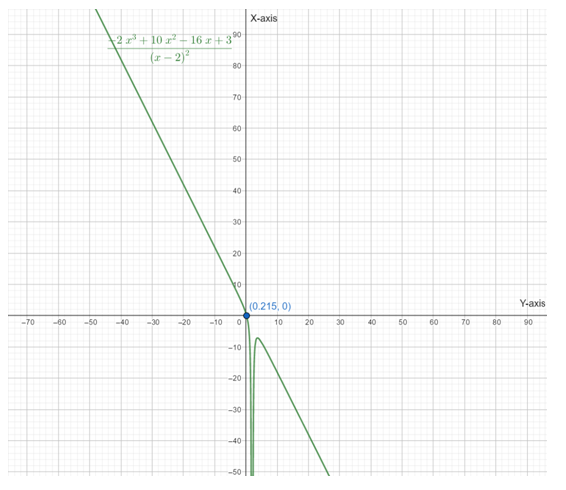
From graph also it is clear that the function
c.
To find the intervals on which the function is concave up by using analytical method.
c.
Answer to Problem 16RE
The Function
Explanation of Solution
Given:
The function is
Calculation:
The graph of a twice differentiable function
Concave up on any interval where
Since,
First derivative :
Second derivative :
Now, put
Therefore , there are four intervals that is
check the value of
Now for
Therefore, the Function
Now for
Therefore, the Function
Now for
Therefore, the Function
Below is the graph of
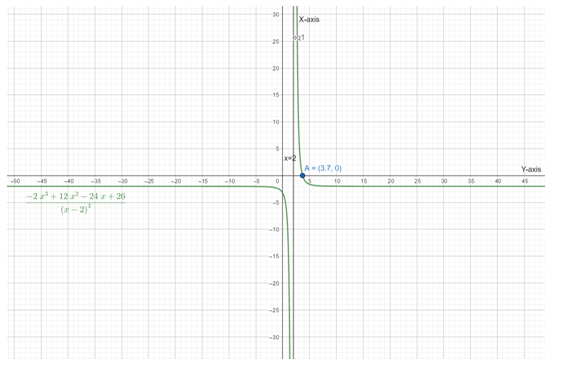
From graph it is clear that the Function
d.
To find the intervals on which the function is concave down by using analytical method.
d.
Answer to Problem 16RE
The Function
Explanation of Solution
Given:
The function is
Calculation:
The graph of a twice differentiable function
Concave up on any interval where
Since,
First derivative :
Second derivative :
Now, put
Therefore , there are three intervals that is
check the value of
Now for
Therefore, the Function
Now for
Therefore, the Function
Now for
Therefore, the Function
Below is the graph of
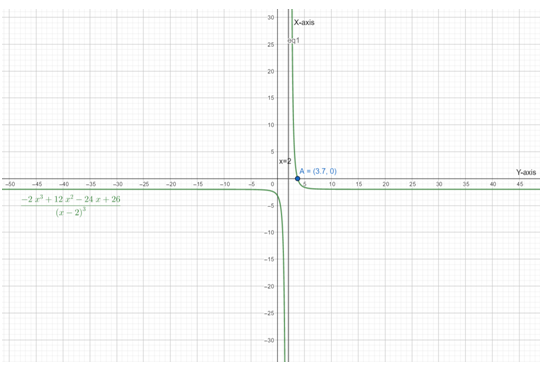
From graph also it is clear that the Function
e.
To find any local extreme values.
e.
Answer to Problem 16RE
The function
Explanation of Solution
Given:
The function is
Calculation:
Graph of
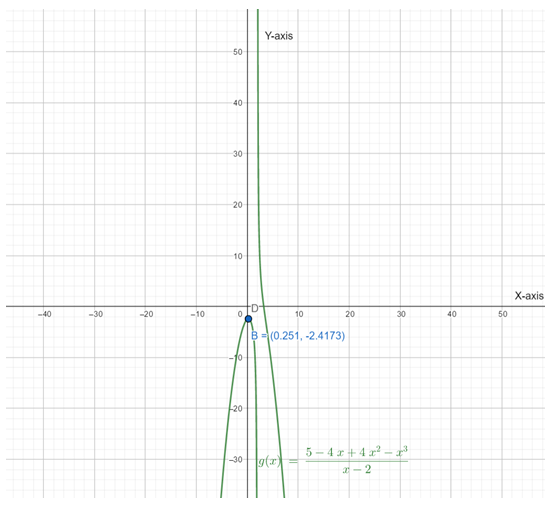
From graph it is clear that the function
f.
To find inflections points.
f.
Answer to Problem 16RE
The inflection point is at
Explanation of Solution
Given:
The function is
Calculation:
Inflection point of any function is a point where the graph of function has a tangent line and where the concavity changes.
Since,
changes concavity in interval
Therefore, theinflection point is at
Chapter 5 Solutions
Calculus 2012 Student Edition (by Finney/Demana/Waits/Kennedy)
Additional Math Textbook Solutions
Elementary Statistics
Intro Stats, Books a la Carte Edition (5th Edition)
Calculus: Early Transcendentals (2nd Edition)
A Problem Solving Approach To Mathematics For Elementary School Teachers (13th Edition)
Calculus: Early Transcendentals (2nd Edition)
Elementary Statistics: Picturing the World (7th Edition)
- Use Laplace transform to solve the initial value problem y' + y = tsin(t), y(0) = 0arrow_forwardThe function g is defined by g(x) = sec² x + tan x. What are all solutions to g(x) = 1 on the interval 0 ≤ x ≤ 2π ? A x = = 0, x == = 3, x = π, x = 7 4 , 4 and x 2π only = B x = 4' 1, x = 1, x = 57 and x = 3 only C x = πk and x = - +πk D , where is any integer П x = +πk and П x = +πk, where k is any integerarrow_forwardVector v = PQ has initial point P (2, 14) and terminal point Q (7, 3). Vector v = RS has initial point R (29, 8) and terminal point S (12, 17). Part A: Write u and v in linear form. Show all necessary work. Part B: Write u and v in trigonometric form. Show all necessary work. Part C: Find 7u − 4v. Show all necessary calculations.arrow_forward
- An object is suspended by two cables attached at a single point. The force applied on one cable has a magnitude of 125 pounds and acts at an angle of 37°. The force on the other cable is 75 pounds at an angle of 150°.Part A: Write each vector in component form. Show all necessary work.Part B: Find the dot product of the vectors. Show all necessary calculations Part C: Use the dot product to find the angle between the cables. Round the answer to the nearest degree. Show all necessary calculations.arrow_forwardAn airplane flies at 500 mph with a direction of 135° relative to the air. The plane experiences a wind that blows 60 mph with a direction of 60°.Part A: Write each of the vectors in linear form. Show all necessary calculations.Part B: Find the sum of the vectors. Show all necessary calculations. Part C: Find the true speed and direction of the airplane. Round the speed to the thousandths place and the direction to the nearest degree. Show all necessary calculations.arrow_forwardUse sigma notation to write the sum. Σ EM i=1 - n 2 4n + n narrow_forward
- Vectors t = 3i + 7j, u = 2i − 5j, and v = −21i + 9j are given.Part A: Find the angle between vectors t and u. Show all necessary calculations. Part B: Choose a value for c, such that c > 1. Find w = cv. Show all necessary work.Part C: Use the dot product to determine if t and w are parallel, orthogonal, or neither. Justify your answer.arrow_forwardA small company of science writers found that its rate of profit (in thousands of dollars) after t years of operation is given by P'(t) = (5t + 15) (t² + 6t+9) ³. (a) Find the total profit in the first three years. (b) Find the profit in the sixth year of operation. (c) What is happening to the annual profit over the long run? (a) The total profit in the first three years is $ (Round to the nearest dollar as needed.)arrow_forwardFind the area between the curves. x= -2, x = 7, y=2x² +3, y=0 Set up the integral (or integrals) needed to compute this area. Use the smallest possible number of integrals. Select the correct choice below and fill in the answer boxes to complete your choice. A. 7 [[2x² +3] dx -2 B. [[ ] dx+ -2 7 S [ ] dx The area between the curves is (Simplify your answer.)arrow_forward
- The rate at which a substance grows is given by R'(x) = 105e0.3x, where x is the time (in days). What is the total accumulated growth during the first 2.5 days? Set up the definite integral that determines the accumulated growth during the first 2.5 days. 2.5 Growth = (105e0.3x) dx 0 (Type exact answers in terms of e.) Evaluate the definite integral. Growth= (Do not round until the final answer. Then round to one decimal place as needed.)arrow_forwardFind the total area of the shaded regions. y 18- 16- 14- 12- 10- 8- 6- y=ex+1-e 4- 2- 0- 2 3 4 5 -2 -4- X ☑ The total area of the shaded regions is (Type an integer or decimal rounded to three decimal places as needed.)arrow_forwardThe graph of f(x), shown here, consists of two straight line segments and two quarter circles. Find the 19 value of f(x)dx. 小 Srxdx. 19 f(x)dx y 7 -7 2 12 19 X ☑arrow_forward
 Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning
Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON
Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
 Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning
Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning





