
Concept explainers
a.
To find the intervals on which the function is increasing by using analytical method.
a.
Answer to Problem 15RE
The function is increasing in interval
Explanation of Solution
Given:
The function is
Calculation:
The function
Now put
So , there are three intervals that is
put
put
put
Therefore , the function is increasing in interval
Below is the graph of
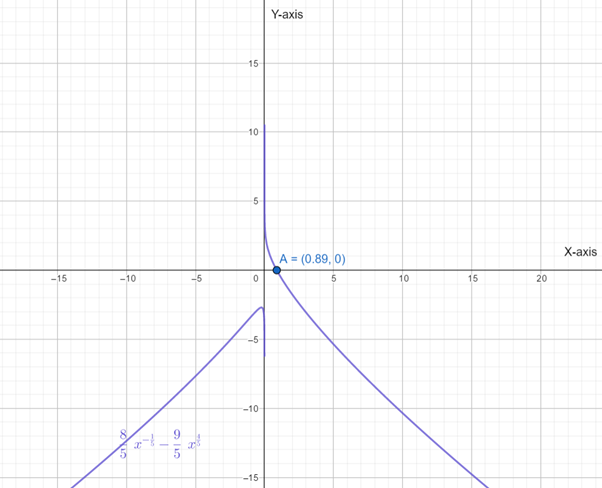
From graph of
b.
To find the intervals on which the function is decreasing by using analytical method.
b.
Answer to Problem 15RE
The function is decreasing in interval
Explanation of Solution
Given:
The function is
Calculation:
The function
Now put
So , there are three intervals that is
put
put
put
Therefore , the function is decreasing in interval
Below is the graph of
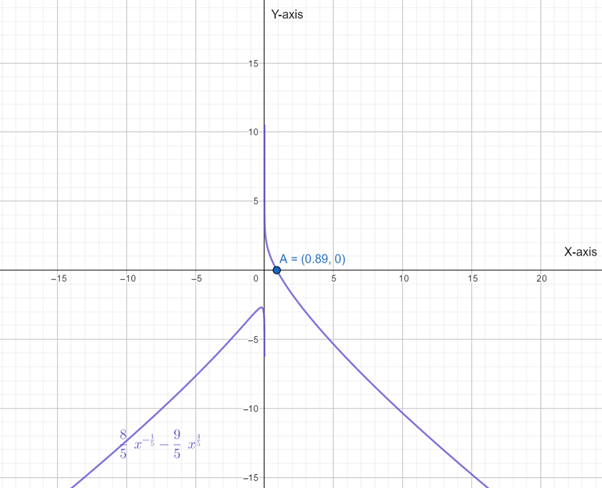
From graph of
c.
To find the intervals on which the function is concave up by using analytical method.
c.
Answer to Problem 15RE
The Function
Explanation of Solution
Given:
The function is
Calculation:
The graph of a twice differentiable function
Concave up on any interval where
Since,
First derivative :
Second derivative :
Now, put
Therefore , there are three intervals that is
check the value of
Now for
Now for
Now for
Therefore, the Function
Below is the graph of
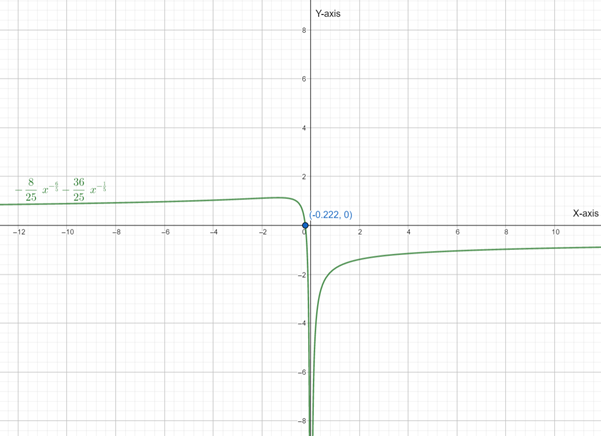
From graph it is clear that, the Function
d.
To find the intervals on which the function is concave down by using analytical method.
d.
Answer to Problem 15RE
The Function
Explanation of Solution
Given:
The function is
Calculation:
The graph of a twice differentiable function
Concave up on any interval where
Since,
First derivative :
Second derivative :
Now, put
Therefore , there are three intervals that is
check the value of
Now for
Now for
Now for
Therefore, the Function
Below is the graph of
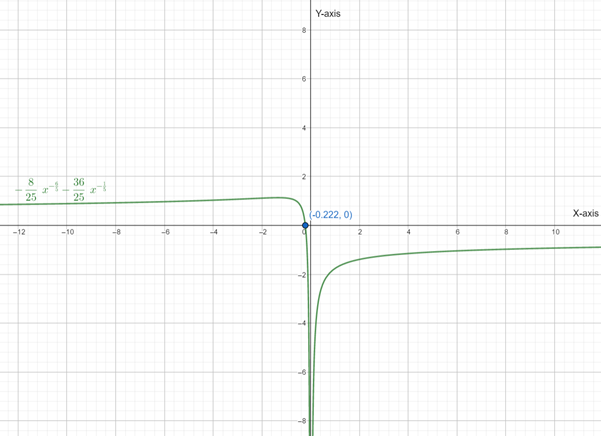
From graph it is clear that, the Function
e.
To find any local extreme values.
e.
Answer to Problem 15RE
The function
Explanation of Solution
Given:
The function is
Calculation:
Graph of
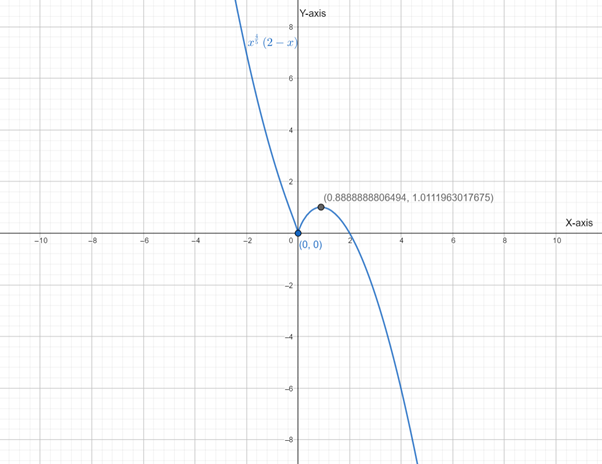
From graph it is clear that the function
f.
To find inflections points.
f.
Answer to Problem 15RE
The inflection point is at
Explanation of Solution
Given:
The function is
Calculation:
Inflection point of any function is a point where the graph of function has a tangent line and where the concavity changes.
Since,
Therefore, the inflection point is at
Chapter 5 Solutions
Calculus 2012 Student Edition (by Finney/Demana/Waits/Kennedy)
Additional Math Textbook Solutions
Pre-Algebra Student Edition
College Algebra (7th Edition)
Introductory Statistics
Algebra and Trigonometry (6th Edition)
- A small company of science writers found that its rate of profit (in thousands of dollars) after t years of operation is given by P'(t) = (5t + 15) (t² + 6t+9) ³. (a) Find the total profit in the first three years. (b) Find the profit in the sixth year of operation. (c) What is happening to the annual profit over the long run? (a) The total profit in the first three years is $ (Round to the nearest dollar as needed.)arrow_forwardFind the area between the curves. x= -2, x = 7, y=2x² +3, y=0 Set up the integral (or integrals) needed to compute this area. Use the smallest possible number of integrals. Select the correct choice below and fill in the answer boxes to complete your choice. A. 7 [[2x² +3] dx -2 B. [[ ] dx+ -2 7 S [ ] dx The area between the curves is (Simplify your answer.)arrow_forwardThe rate at which a substance grows is given by R'(x) = 105e0.3x, where x is the time (in days). What is the total accumulated growth during the first 2.5 days? Set up the definite integral that determines the accumulated growth during the first 2.5 days. 2.5 Growth = (105e0.3x) dx 0 (Type exact answers in terms of e.) Evaluate the definite integral. Growth= (Do not round until the final answer. Then round to one decimal place as needed.)arrow_forward
- Find the total area of the shaded regions. y 18- 16- 14- 12- 10- 8- 6- y=ex+1-e 4- 2- 0- 2 3 4 5 -2 -4- X ☑ The total area of the shaded regions is (Type an integer or decimal rounded to three decimal places as needed.)arrow_forwardThe graph of f(x), shown here, consists of two straight line segments and two quarter circles. Find the 19 value of f(x)dx. 小 Srxdx. 19 f(x)dx y 7 -7 2 12 19 X ☑arrow_forwardCan you solve this two numerical method eqn and teach me.arrow_forward
- Find the area between the following curves. x=-4, x=2, y=ex, and y = 3 - ex Set up the integral (or integrals) needed to compute this area. Use the small (Type exact answers in terms of e.) 3 In 2 A. S √ [3-2e*] dx+ -4 2 S [2ex-3] dx 3 In 2 B. dx Find the area between the curves. Area = (Type an exact answer in terms of e.)arrow_forwardUse the definite integral to find the area between the x-axis and f(x) over the indicated interval. Check first to see if the graph crosses the x-axis in the given interval. f(x)=8-2x²: [0,4] Set up the integral (or integrals) needed to compute this area. Use the smallest possible number of integrals. Select the correct choice below and fill in the answer boxes to ○ A. dx B. 2 S 8-2x² dx+ 4 S 2 8-2x2 dx C. dx + S dx For the interval [0,4], the area between the x-axis and f(x) is (Type an integer or a simplified fraction.)arrow_forwardPollution from a factory is entering a lake. The rate of concentration of the pollutant at time t is 5 given by P'(t) = 126t², where t is the number of years since the factory started introducing pollutants into the lake. Ecologists estimate that the lake can accept a total level of pollution of 600 units before all the fish life in the lake ends. Can the factory operate for 2 years without killing all the fish in the lake? Set up the integral that would determine the pollution level after 2 years. 2 5 126t 2 dt Can the factory operate for 2 years without killing all the fish in the lake? Thee factory can operate for 2 years without killing all the fish in the lake because the value of the integral is , which is less than 600. (Round to the nearest integer as needed.)arrow_forward
- Use the definite integral to find the area between the x-axis and f(x) over the indicated interval. Check first to see if the graph crosses the x-axis in the given interval. f(x)=4x-12; [2,6] The area between the x-axis and f(x) is (Type an integer or a simplified fraction.)arrow_forwardEvaluate the definite integral. 70 √5√2-6 3 dz 70 S 5√2-6 dz= 7 江 (Type an integer or decimal rounded to two decimal places as needed.)arrow_forwardFind the area between the following curves. 2 y=x³-x²+x+4; y=5x² -7x+4 The area between the curves is (Simplify your answer.) ...arrow_forward
 Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning
Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON
Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
 Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning
Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning





