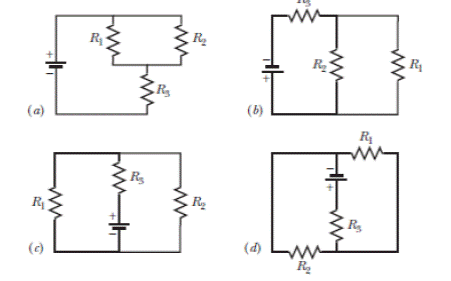
Problem 1Q: a In Fig. 27-18a, with R1R2, is the potential difference across R2 more than, less than, or equal to... Problem 2Q: a In Fig. 27-18a, are resistors R1 and R3 in series? b Are resistors R1 and R2 in parallel? c Rank... Problem 3Q: You are to connect resistors R1 and R2, with R1R2, to a battery, first individually, then in series,... Problem 4Q: In Fig. 27-19, a circuit consists of a battery and two uniform resistors, and the section lying... Problem 5Q: For each circuit in Fig 27-20, are the resistors connected in series, in parallel, or neither?... Problem 6Q: Res-monster maze. In Fig. 27-21, all the resistors have a resistance of 4.0 and all the ideal... Problem 7Q: A resistor R1 is wired to a battery, then resistor R2 is added in series. Are a the potential... Problem 8Q: What is the equivalent resistance of three resistors, each or resistance R, if they are connected to... Problem 9Q: Two resistors are wired to a battery. a In which arrangement, parallel or series, are the potential... Problem 10Q: Cap-monster maze. In Fig. 27-22, all the capacitors have a capacitance of 6.0F, and all the... Problem 11Q: Initially, a single resistor, R1 is wired to a battery. Then resistor R2 is added in parallel. Are a... Problem 12Q: After the switch in Fig. 27-15 is closed on point a, there is current i through resistance R. Figure... Problem 13Q: Figure 27-24 shows three sections of circuit that are to be connected in turn to the same battery... Problem 1P: SSM WWW In Fig. 27-25, the ideal batteries have emfs 1 = 12 V and 2= 6.0 V. What are a the current,... Problem 2P: In Fig. 27-26, the ideal batteries have emfs 1 = 150 V and 2 = 50 V and the resistances are R1 = 3.0... Problem 3P: ILW A car battery with a 12 V emf and an internal resistance of 0.040 is being charged with a... Problem 4P: GO Figure 27-27 shows a circuit of four resistors that are connected to a larger circuit. The graph... Problem 5P: A 5.0 A current is set up in a circuit for 6.0 min by a rechargeable battery with a 6.0 V emf. By... Problem 6P: A standard flashlight battery can deliver about 2.0 W h of energy before it runs down, a If a... Problem 7P: A wire of resistance 5.0 is connected to a battery whose emf is 2.0 V and whose internal... Problem 8P: A certain car battery with a 12.0 V emf has an initial charge of 120 Ah. Assuming that the potential... Problem 9P: a In electron-volts, how much work does an ideal battery with a 12.0 V emf do on an electron that... Problem 10P: a In Fig. 27-28, what value must R have if the current in the circuit is to be 1.0mA? Take 1 = 2.0... Problem 11P: SSM In Fig. 27-29, circuit section AB absorbs energy at a rate of 50 W when current i = 1.0 A... Problem 12P: Figure 27-30 shows a resistor of resistance R = 6.00 connected to an ideal battery of emf = 12.0 V... Problem 13P: A 10-km-long underground cable extends east to west and consists of two parallel wires, each of... Problem 14P: GO In Fig. 27-32a, both batteries have emf = 1.20 V and the external resistance R is a variable... Problem 15P: ILW The current in a single-loop circuit with one resistance R is 5.0 A. When an additional... Problem 16P: A solar cell generates a potential difference of 0.10 V when a 500 resistor is connected across it,... Problem 17P: SSM In Fig. 27-33, battery 1 has emf 1 = 12.0 V and internal resistance r1 = 0.016 and battery 2... Problem 18P: In Fig. 27-9, what is the potential difference Vd Ve between points d and c if 1 = 4.0 V, 2 = 1.0... Problem 19P: A total resistance of 3.00 is to be produced by connecting an unkown resistance to a 12.0 ... Problem 20P: When resistors 1 and 2 are connected in series, the equivalent resistance is 16.0 . When they are... Problem 21P Problem 22P: Figure 27-34 shows five 5.00 resistors. Find the equivalent resistance between points a Fand H and... Problem 23P: In Fig. 27-35, R1 = 100 , R2 = 50 , and the ideal batteries have emfs 1 = 6.0 V, 2 = 5.0 V, and 3 =... Problem 24P: In Fig. 27-36, R1 = R2 = 4.00 and R3 = 2.50 . Find the equivalent resistance between points D and... Problem 25P: SSM Nine copper wires of length l and diameter d are connected in parallel to form a single... Problem 26P: Figure 27-37 shows a battery connected across a uniform resistor R0. A sliding contact can move... Problem 27P: Side flash. Figure 27-38 indicates one reason no one should stand under a tree during a lightning... Problem 28P: The ideal battery in Fig. 27-39a has emf = 6.0 V. Plot 1 in Fig. 27-39b gives the electric... Problem 29P: In Fig. 27-40, R1 = 6.00 , R2 = 18.0 , and the ideal battery has emf = 12.0 V. What are the a size... Problem 30P: GO In Fig. 27-41, the ideal batteries have emfs 1 = 10.0 V and 2= 0.50011, and the resistances are... Problem 31P: SSMGO In Fig. 27-42, the ideal batteries have emfs 1 = 5.0 V and 2 = 12 V, the resistances are each... Problem 32P: Both batteries in Fig. 27-43a are ideal. Emf 1 of battery 1 has a fixed value, but emf 2 of battery... Problem 33P: GO In Fig. 27-44. the current in resistance 6 is i6 = 1.40 A and the resistances are R1 = R2 = R3 =... Problem 34P: The resistances in Figs. 27-45a and b are all 6.0 . and the batteries are ideal 12 V batteries, a... Problem 35P: GO In Fig. 27-46, = 12.0 V, R1, = 2000 , R2 = 3000 , and R3 = 4000 . What are the potential... Problem 36P: GO In Fig. 27-47, 1 = 6.00 V, 2 = 12.0 V, R1, = 100 , R2 = 200 and R3 = 300 . One point of the... Problem 37P: In Fig. 27-48, the resistances are R1 = 2.00 , R2 = 5.00 , and the battery is ideal. What value of... Problem 38P: Figure 27-49 shows a section of a circuit. The resistances are R1 = 2.0 , R2 = 4.0 , and R3 = 6.0 ,... Problem 39P: GO In Fig. 27-50, two batteries with an emf = 12.0 V and an internal resistance r = 0.300 are... Problem 40P: GO Two identical batteries of emf = 12.0 V and internal resistance r = 0.200 are to be connected... Problem 41P: In Fig. 27-41, 1 = 3.00 V, 2 = 1.00 V, R1 = 4.00 , R3 = 5.00 , and both batteries are ideal. What is... Problem 42P: In Fig. 27-52, an array of n parallel resistors is connected in series to a resistor and an ideal... Problem 43P: You are given a number of 10 resistors, each capable of dissipating only 1.0 W without being... Problem 44P: GO In Fig. 27-53, R1 = 100 , R2 = R3 = 50.0 , R4 = 75.0 , and the ideal battery has emf = 6.00 V. a... Problem 45P: ILW In Fig. 27-54, the resistances are R1 = 1.0 and R2 = 2.0 , and the ideal batteries have emfs 1... Problem 46P: In Fig. 27-55a, resistor 3 is a variable resistor and the ideal battery has emf = 12 V. Figure... Problem 47P: SSM A copper wire of radius a = 0.250 mm has an aluminum jacket of outer radius b = 0.380 mm. There... Problem 48P: GO In Fig. 27-53, the resistors have the values R1 = 7.00 , R2 = 12.0 , and R3 = 4.00 , and the... Problem 49P: ILW a In Fig. 27-56, what current does the ammeter read if = 5.0 V ideal battery, R1 = 2.0 , R2 =... Problem 50P: In Fig. 27-57, R1 = 2.00R, the ammeter resistance is zero, and the battery is ideal. What multiple... Problem 51P: In Fig. 27-58, a voltmeter of resistance Rv= 300 and an Ammeter of resistance RA = 3.00 are being... Problem 52P: A simple ohmmeter is made by connecting a 1.50V flashlight battery in series with a resistance R and... Problem 53P: In Fig. 27-14, assume that = 3.0 V, r = 100 , R1 = 250 , and R2 = 300 . If the voltmeter resistance... Problem 54P: When the lights of a car are switched on, an ammeter in series with them reads 10.0 A and a... Problem 55P: In Fig. 27-61, Rsis to be adjusted in value by moving the sliding contact across it until points a... Problem 56P: In Fig. 27-62. a voltmeter of resistance Rv = 300 and an ammeter of resistance RA = 3.00 are being... Problem 57P: Switch S in Fig. 27-63 is closed at time t = 0, to begin charging an initially uncharged capacitor... Problem 58P: In an RC series circuit, emf = 12.0 V, resistance R = 1.40 M, and capacitance C = 1.80 F. a... Problem 59P: SSM What multiple of the time constant gives the time taken by an initially uncharged capacitor in... Problem 60P: A capacitor with initial charge q0 is discharge through a resistor. What multiple of the time... Problem 61P: ILW A 15.0 k resistor and a capacitor are connected in series, and then a 12.0 V potential... Problem 62P: Figure 27-64 shows the circuit of a flashing lamp, like those attached to barrels at highway... Problem 63P: SSM WWWIn the circuit of Fig. 27-65, = 1.2 kV, C= 6.5 F, R1 = R2 = R3 = 0.73 M. With C completely... Problem 64P: A capacitor with an initial potential difference of 100 V is discharged through a resistor when a... Problem 65P: GO In Fig. 27-66. R1 = 10.0 k, R2 = 15.0 k, C= 0.400 F, and the ideal battery has emf = 20.0 V.... Problem 66P: Figure 27-67 display two circuits with a charged capacitor that is to be discharged through a... Problem 67P: The potential difference between the plates of a leaky meaning that charge leaks from one plate to... Problem 68P: A 1.0 F capacitor with an initial stored energy of 0.50 J is discharged through a 1.0 M resistor. a... Problem 69P: GO A 3.00 M resistor and a 1.00 F capacitor are connected in series with an ideal battery of emf =... Problem 70P: GO Each of the six real batteries in Fig. 27-68 has an emf of 20 V and a resistance of 4.0 . a What... Problem 71P: In Fig. 27-69, R1 = 20.0 , R2 = 10.0 , and the ideal battery has emf = 120 V. What is the current... Problem 72P: In Fig.27-70, the ideal battery has emf = 30.0 V, and the resistances are R1 = R2 = 14 , R3 = R4 =... Problem 73P: SSM Wires A and B, having equal lengths of 40.0 m and equal diameters of 2.60 mm, are connected in... Problem 74P: What are the a size and b direction up or down of current i in Fig. 27-71, where all resistances are... Problem 75P: Suppose that, while you are sitting in a chair, charge separation between your clothing and the... Problem 76P: GO In Fig. 27-72, the ideal batteries have emfs 1 = 20.0 V, 2 = 10.0 V, and 3 = 50. V, and the... Problem 77P: SSM A temperature-stable resistor is made by connecting a resistor made of silicon in series with... Problem 78P: In Fig. 27-14, assume that = 5.0 V, r = 2.0 , R1 = 5.0 , and R2 = 4.0 . If the ammeter resistance... Problem 79P: SSM An initially uncharged capacitor C is fully charged by a device of constant emf connected in... Problem 80P: In Fig. 27-73, R1 = 5.00 , R2 = 10.0 , R3 = 15.0 , C1 = 5.00 F, C2=10.0 F, and the ideal battery has... Problem 81P: In Fig. 27-5a, find the potential difference across R2 if = 12 V, R1 = 3.0 , R2 = 4.0 , and R3 = 5.0 Problem 82P: In Fig. 27-8a, calculate the potential difference between aand c by considering a path that contains... Problem 83P: SSM A controller on an electronic arcade game consists of a variable resistor connected across the... Problem 84P: An automobile gasoline gauge is shown schematically in Fig. 27-74. The indicator on the dashboard... Problem 85P: SSM The starting motor of a car is turning too slowly, and the mechanic has to decide whether to... Problem 86P: Two resistors R1 and R2 may be connected either in series or in parallel across an ideal battery... Problem 87P: The circuit of Fig. 27-25 shows a capacitor, two ideal batteries, two resistors, and a switch S.... Problem 88P: In Fig. 27-41, R1 = 10.0 , R2 = 20.0 , and the ideal batteries have emfs 1 = 20.0 V and 2 = 50.0 V.... Problem 89P: In Fig. 27-76, R= 10 . what is the equivalent resistance between points A and B? Hint: This circuit... Problem 90P: a In Fig. 27-4a, show that the rate at which energy is dissipated in R as thermal energy is a... Problem 91P: In Fig. 27-77, the ideal batteries have emfs 1 = 12.0 V and 2 = 4.00 V, and the resistances are each... Problem 92P: Figure 27-28 shows a portion of a circuit through which there is a current I = 6.00 A. The... Problem 93P: Thermal energy is to be generated in a 0.10 resistor at the rate of 10 W by connecting the resistor... Problem 94P: Figure 27-29 shows three 20.0 resistors. Find the equivalent resistance between points a A and B, b... Problem 95P: A 120 V power line is protected by a 15 A fuse. What is the maximum number of 500 W lamps that can... Problem 96P: Figure 27-63 shows an ideal battery of emf = 12 V, a resistor of resistance R = 4.0 , and an... Problem 97P: SSM A group of N identical batteries of emf and internal resistance r may be connected all in... Problem 98P: SSM In Fig. 27-48, R1 = R2 = 10.0 , and the ideal battery has emf = 12.0 V. a What value of R3... Problem 99P: SSM In Fig. 27-66, the ideal battery has emf = 30 V, the resistances are R1 =20 k and R2 = 10 k,... Problem 100P: In Fig. 27-81, the ideal batteries have emfs 1 = 20.0 V, 2 = 10.0 V, 3 = 5.00 V, and 4 = 5.00 V, and... Problem 101P: In Fig. 27-82, an ideal battery of emf = 12.0 V is connected to a network of resistances R1= 6.00 ,... Problem 102P: The following table gives the electric potential difference VTacross the terminals of a battery as a... Problem 103P: In Fig. 27-83, 1 = 6.00 V, 2 = 12.0 V, R1= 200 and R2 = 100 . What are the a size and b direction... Problem 104P: A three-way 120 V lamp bulb that contains two filaments is rated for 100-200-300 W. One filament... Problem 105P: In Fig. 27-84, R1 = R2 = 2.0 , R3 = 4.0 , R4 = 3.0 , R5 =1.0 and R6 = R7 = R8 = 8.0, and the ideal... format_list_bulleted

 Physics for Scientists and Engineers, Technology ...PhysicsISBN:9781305116399Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers, Technology ...PhysicsISBN:9781305116399Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning College PhysicsPhysicsISBN:9781285737027Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning
College PhysicsPhysicsISBN:9781285737027Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning
Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning College PhysicsPhysicsISBN:9781305952300Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning
College PhysicsPhysicsISBN:9781305952300Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning College PhysicsPhysicsISBN:9781938168000Author:Paul Peter Urone, Roger HinrichsPublisher:OpenStax College
College PhysicsPhysicsISBN:9781938168000Author:Paul Peter Urone, Roger HinrichsPublisher:OpenStax College Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning




