
Concept explainers
a.
To find: The possible rational zeroes of the function
a.
Answer to Problem 40E
Possible rational zeroes of the function are
Explanation of Solution
Given information:
Given function is
Formula used:
Rational root test: According to this test, the list of all possible rational zeroes of a polynomial is,
Possible zeroes
Consider the function as,
Here, leading coefficient is
Factors of constant term 4 are
Factors of leading coefficient
Then possible rational zeroes are,
Therefore, possible rational zeroes of the function are
b.
To draw: The graph of the function
b.
Explanation of Solution
Given information:
Given function is
Possible rational zeroes of the function are
Consider the function as
Graph of the function can be drawn as,
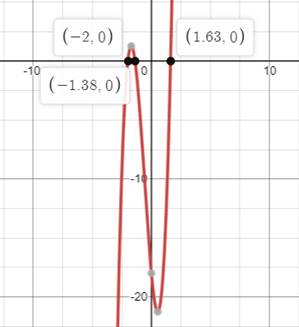
From the graph of the function, it is clear that zeroes of the function are
c.
All the real zeroes of the function
c.
Answer to Problem 40E
Real zeroes of the function are
Explanation of Solution
Given information:
Given function
Possible rational zeroes of the function are
Consider the given function as function
From part (a), possible rational zeroes of the function are
From part (b), it is clear is clear that the curve do not touch x − axis at
Hence, real zeroes of the function are
Chapter 2 Solutions
EBK PRECALCULUS W/LIMITS
- 2. Consider the following: Prove that x, x2, and 1/x are the solutions to the homogeneous equation corresponding to x³y"" + x²y" + 2xy' + 2y = 2x4. b. use variation of parameters to find a particular solution and complete the general solution to the differential equation. I am interested in process. You may use a computer for integration, finding determinants and doing Kramer's.arrow_forward3. A spring is stretched 6 in. by a mass that weighs 8 lb. The mass is attached to a dashpot mechanism that has a damping constant of 0.25 lb-sec./ft. and is acted on by an external force of 4 cos 2t lb. a. Set-up the differential equation and initial value problem for the system. b. Write the function in phase-amplitude form. C. Determine the transient solution to the system. Show your work. d. Determine the steady state of this system. Show your work. e. Is the system underdamped, overdamped or critically damped? Explain what this means for the system.arrow_forward4. Suppose that you have a circuit with a resistance of 20, inductance of 14 H and a capacitance of 11 F. An EMF with equation of E(t) = 6 cos 4t supplies a continuous charge 60 to the circuit. Suppose that the q(0)= 8 V and the q'(0)=7. Use this information to answer the following questions a. Find the function that models the charge of this circuit. b. Is the circuit underdamped, overdamped or critically damped?arrow_forward
- 1. Solve the initial value problem: y" -11y' + 30y = x³e6x y(0) 11, y'(0) = 36 =arrow_forwardWhat is the particular solution to the differential equation y′′ + y = 1/cos t ?arrow_forwardWhich of the following is the general solution to y′′ + 4y = e^2t + 12 sin(2t) ?A. y(t) = c1 cos(2t) + c2 sin(2t) + 1/8 e^2t − 3t cos(2t)B. y(t) = c1e^2t + c2e^−2t + 1/4 te^2t − 3t cos(2t)C. y(t) = c1 + c2e^−4t + 1/12 te^2t − 3t cos(2t)D. y(t) = c1 cos(2t) + c2 sin(2t) + 1/8 e^2t + 3 sin(2t)E. None of the above. Please include all steps! Thank you!arrow_forward
- Show that i cote +1 = cosec 20 tan 20+1 = sec² O २ cos² + sin 20 = 1 using pythagon's theoremarrow_forwardFind the general solution to the differential equationarrow_forwardcharity savings Budget for May travel food Peter earned $700 during May. The graph shows how the money was used. What fraction was clothes? O Search Submit clothes leisurearrow_forward
- Exercise 11.3 A slope field is given for the equation y' = 4y+4. (a) Sketch the particular solution that corresponds to y(0) = −2 (b) Find the constant solution (c) For what initial conditions y(0) is the solution increasing? (d) For what initial conditions y(0) is the solution decreasing? (e) Verify these results using only the differential equation y' = 4y+4.arrow_forwardAphids are discovered in a pear orchard. The Department of Agriculture has determined that the population of aphids t hours after the orchard has been sprayed is approximated by N(t)=1800−3tln(0.17t)+t where 0<t≤1000. Step 1 of 2: Find N(63). Round to the nearest whole number.arrow_forward3. [-/3 Points] DETAILS MY NOTES SCALCET8 7.4.032. ASK YOUR TEACHER PRACTICE ANOTHER Evaluate the integral. X + 4x + 13 Need Help? Read It SUBMIT ANSWER dxarrow_forward
 Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning
Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON
Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
 Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning
Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning





