Chapter 20, Problem 47P

To determine

The magnetic field along the x -axis between both the wires as a function of x .

Answer to Problem 47P

Magnetic field varying from first wire to another on positive x -axis is

  ${\overrightarrow{B}}_{net}=\frac{{\mu }_{0}I}{2\pi x}-\frac{{\mu }_{0}I}{2\pi (d-x)}$

Explanation of Solution

Given:

Two long parallel wires carrying equal current in the same direction at a distance d apart as shown below.

  

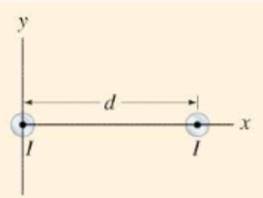
Formula used:

The magnetic field is calculated as

  $\overrightarrow{B}=\frac{{\mu }_{0}I}{2\pi d}$

Calculation:

Magnetic field varying from first wire to another on positive x -axis is

  ${\overrightarrow{\text{B}}}_{\text{net}}=\frac{{\mu }_0\text{I}}{2\pi \text{x}}-\frac{{\mu }_0\text{I}}{2\pi (\text{d}-\text{x})}$

  

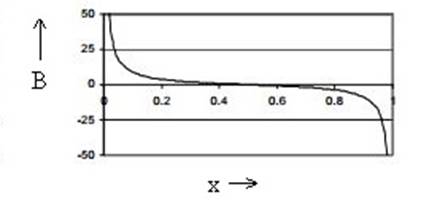
Due to first wire, magnetic field will be caused towards positive y -axis. Now, moving away from the wire, there will be decrease in magnitude of the magnetic field. But, due to another wire distance at distance d apart, another magnetic field will be experienced. The current in the other wire is in the same direction. So, moving towards positive x -axis, the magnetic field induced by second wire will counteract with the magnetic field induced by first wire. Thus, the magnetic field will keep decreasing while moving towards negative y -axis.

Conclusion:

Magnetic field varying from first wire to another on positive x -axis is

  ${\overrightarrow{B}}_{net}=\frac{{\mu }_{0}I}{2\pi x}-\frac{{\mu }_{0}I}{2\pi (d-x)}$