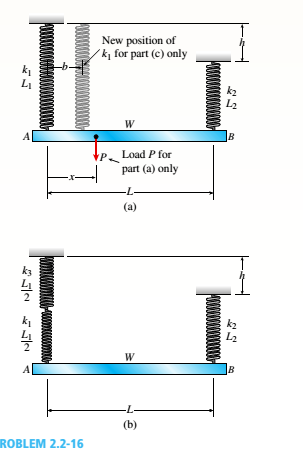
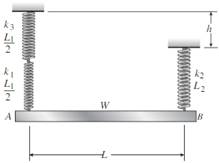
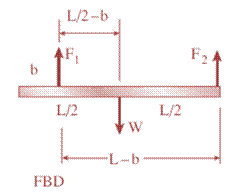
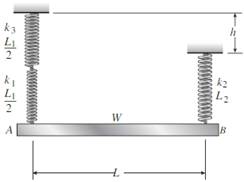
Problem 2.2.1P: A 10-ft rigid bar AB is supported with a vertical translational spring at A and a pin at B. The bar... Problem 2.2.2P: Rigid bar ABC is supported with a pin at A and an elastic steel rod at C. The elastic rod has a... Problem 2.2.3P: The L-shaped arm ABCD shown in the figure lies in a vertical plane and pivots about a horizontal pin... Problem 2.2.4P: A steel cable with a nominal diameter of 25 mm (see Table 2-1) is used in a construction yard to... Problem 2.2.5P: A steel wire- and an aluminum allay wire have equal lengths, and support equal loads P (see figure).... Problem 2.2.6P: By what distance h does the cage shown in the figure move downward when the weight W is placed... Problem 2.2.7P: Rigid bar ACB is supported by an elastic circular strut DC having an outer diameter of 15 in. and... Problem 2.2.8P: A plastic cylinder is held snugly between a rigid plate and. a foundation by two steel bolts (see... Problem 2.2.9P: A safety valve on the top of a tank containing steam under pressure p has a discharge hole of... Problem 2.2.10P: The device shown in the figure consists of a prismatic rigid pointer ABC supported by a uniform... Problem 2.2.11P: A small lab scale has a rigid L-shaped frame ABC consisting of a horizontal arm AB (length b = 10... Problem 2.2.12P: A small lab scale has a rigid L-shaped frame ABC consisting of a horizontal aim AB (length b = 30... Problem 2.2.13P: Two rigid bars are connected to each other by two linearly elastic springs. Before loads are... Problem 2.2.14P: The three-bar truss ABC shown in the figure part a has a span L = 3 m and is constructed of steel... Problem 2.2.15P: An aluminum wire having a diameter d = 1/10 in. and length L = 12 ft is subjected to a tensile load... Problem 2.2.16P: A uniform bar AB of weight W = 25 N is supported by two springs, as shown in the figure. The spring... Problem 2.2.17P: A hollow, circular, cast-iron pipe (Ec =12,000 ksi) supports a brass rod (Ec= 14,000 ksi} and weight... Problem 2.2.18P: The horizon Lai rigid beam A BCD is supported by vertical bars BE and CF and is loaded by vertical... Problem 2.2.19P: Two pipe columns (AB, FC) are pin-connected to a rigid beam (BCD), as shown in the figure. Each pipe... Problem 2.2.20P: A framework ABC consists of two rigid bars AB and BC. Each having a length b (see the first part of... Problem 2.2.21P: Solve the preceding problem for the following data: b = 8.0 in., k = 16 lb/in., a = 45°, and P = 10... Problem 2.3.1P: The length of the end segments of the bar (see figure) is 20 in. and the length of the prismatic... Problem 2.3.2P: A long, rectangular copper bar under a tensile load P hangs from a pin that is supported by two... Problem 2.3.3P: An aluminum bar AD (see figure) has a cross-sectional area of 0.40 in- and is loaded by Forces Pi=... Problem 2.3.4P: A vertical bar consists of three prismatic segments A\, A,, and A3with cross-sectional areas of 6000... Problem 2.3.5P: A vertical bar is loaded with axial loads at points B, C, and D. as shown in the figure. The bar is... Problem 2.3.6P: Repeat Problem 2.3-4, but now include the weight of the bar. Sec Table 1.1 in Appendix I for the... Problem 2.3.7P: -7 Repeat Problem 2.3-5, but n include the weight of the bar. See Table I-I in Appendix I for the... Problem 2.3.8P: A rectangular bar of length L has a slot in the middle half of its length (see figure). The bar has... Problem 2.3.9P: Solve the preceding problem if the axial stress in the middle region is 24,000 psi, the length is 30... Problem 2.3.10P: A two-story building has steel columns AB in the first floor and BC in the second floor, as shown in... Problem 2.3.11P: A steel bar is 8.0 Ft long and has a circular cross section of diameter d1= 0.75 in. over one-half... Problem 2.3.12P: A bar ABC of length L consists of two parts of equal lengths but different diameters. Segment AB has... Problem 2.3.13P: A woodpile, driven into the earth, supports a load P entirely by friction along its sides (see... Problem 2.3.14P: Consider the copper lubes joined in the strength of the copper is err = 200 MPa, figure using a... Problem 2.3.15P: The nonprismalic cantilever circular bar shown has an internal cylindrical hole of diameter dtl From... Problem 2.3.16P: *16 A prismatic bar AB of length L, cross-sectional area A, modulus of elasticity E, and weight... Problem 2.3.17P: A flat bar of rectangular cross section, length L, and constant thickness t is subjected to tension... Problem 2.3.18P: A flat brass bar has length L, constant thickness t, and a rectangular cross section whose width... Problem 2.3.19P: Repeat Problem 2.3-18, but assume that the bar is made of copper alloy. Calculate the displacements... Problem 2.3.20P: Repeat Problem 2.3-18, but assume that the bar is made of aluminum alloy. If P2= 200 kN, what is... Problem 2.3.21P: A slightly tapered bar AB of solid circular crass section and length L is supported at end B and... Problem 2.3.22P: A circular aluminum alloy bar of length L = 1.8 m has a slot in the middle half of its length (see... Problem 2.3.23P: A long, slender bar in the shape of a right circular cone with length L and base diameter d hangs... Problem 2.3.24P: A post AB supporting equipment in a laboratory is tapered uniformly throughout its height H (see... Problem 2.3.25P: The main cables of a suspension bridge (see figure part a) follow a curve that is nearly parabolic... Problem 2.3.26P: A uniformly tapered lube AB of circular cross section and length L is shown in the figure. The... Problem 2.3.27P: A vertical steel bar ABC is pin-supported at its upper end and loaded by a force Ptat its lower end.... Problem 2.3.28P: A T-frame structure is torn posed of a prismatic beam ABC and a nonprismatic column DBF. The beam... Problem 2.3.29P: A T-frame structure is composed of prismatic beam ABC and nonprismatic column DBF that are joined at... Problem 2.3.30P: Repeat Problem 2.3-29 if vertical load P at D is replaced by a horizontal load P at D (see figure). Problem 2.3.31P: A bar ABC revolves in a horizontal plane about a vertical axis at the midpoint C (see figure). The... Problem 2.4.1P: The assembly shown in the figure consists of a brass core (diameter d:= 0.25 in.) surrounded by a... Problem 2.4.2P: A cylindrical assembly consisting of a brass core and an aluminum collar is compressed by a load P... Problem 2.4.3P: A steel bar with a uniform cross section, is fixed at both ends. A load P = 2.5 tips is applied at... Problem 2.4.4P: A horizontal rigid bar ABC is pinned at end A and supported by two cables at points B and C. A... Problem 2.4.5P: A solid circular steel cylinder S is encased in a hollow circular aluminum tube A. The cylinder and... Problem 2.4.6P: Three prismatic bars, two of material A and one of material B. transmit a tensile load P (see... Problem 2.4.7P: A circular bar ACB of a diameter d having a cylindrical hole of length .r and diameter till from A... Problem 2.4.8P: Bar ABC is fixed at both ends (see figure) and has load P applied at B. Find reactions at A and C... Problem 2.4.9P: Repeat Problem 2.4-8, but assume that the bar is made of aluminum alloy and that BC is prismatic.... Problem 2.4.10P: A plastic rod AB of length L = 0.5 m has a diameter d1= 30 mm (see figure). A plastic sleeve CD of... Problem 2.4.11P: 2.4-11 Three steel cables jointly support a load of 12 kips (see figure). The diameter of the middle... Problem 2.4.12P: The fixed-end bar ABCD consists of three prismatic segments, as shown in the figure. The end... Problem 2.4.13P: A lube structure is acted on by loads at B and D, as shown in the figure. The tubes are joined using... Problem 2.4.14P: A hollow circular pipe (see figure} support s a load P that is uniformly distributed around a cap... Problem 2.4.15P: The aluminum and steel pipes shown in the figure are Fastened to rigid supports at ends A and B and... Problem 2.4.16P: A rigid bar of weight W = SOO N hangs from three equally spaced vertical wines( length L = 150 mm,... Problem 2.4.17P: A bimetallic bar (or composite bar) of square cross sec lion with dimensions 2b X lb is construe ted... Problem 2.4.18P: S Three-bar truss ABC (see figure) is constructed of steel pipes having a cross-sectional area A =... Problem 2.4.19P: A horizontal rigid bar of weight If' = 72001b is supported by three slender circular rods that are... Problem 2.4.20P: A rigid bar ABCD is pinned at point B and supported by springs at A and D (see figure). The springs... Problem 2.4.21P: A rigid bar AB if of a length B = 66 in. is. hinged to a support at A and supported by two vertical... Problem 2.4.22P: Find expressions For all support reaction forces in the plane frame with load 2P applied at C, as... Problem 2.4.23P: A trimetallic bar is uniformly compressed by an axial force P = 9 kips applied through a rigid end... Problem 2.4.24P: Find expressions for all support reaction Forces in the plane frame with load 3P applied at C as... Problem 2.5.1P: The rails of a railroad track are welded together at their ends (to form continuous rails and thus... Problem 2.5.2P: A circular steel rod of diameter d is subjected to a tensile force P = 3.5 kN (see figure). The... Problem 2.5.3P: A rigid bar of weight W = 750 lb hangs from three equally spaced wires: two of steel and one of... Problem 2.5.4P: A steel rod. of 15-mm diameter is held snugly (but without am1 initial stresses) between rigid walls... Problem 2.5.5P: A bar AB of length L is held between rigid supports and heated no uniformly in such a manner that... Problem 2.5.6P: A beam is constructed using two angle sections (L 102 × 76 × 6.4) arranged back to back, as shown in... Problem 2.5.7P: A W 8 × 28 beam of a length 10 ft is held between immoveable supports. The beam has a modulus of... Problem 2.5.8P: A plastic bar ACB having two different solid circular cross sections is held between rigid supports,... Problem 2.5.9P: ,5-9 A flat aluminum alloy bar is fixed at both ends. Segment AB has a slight taper. If the... Problem 2.5.10P: Repeat Problem 2.5-9 for the flat bar shown in the figure but assume that and that Problem 2.5.11P: A circular steel rod AB? (diameter d, = 1.0 in., length L1= 3.0 Ft) has a bronze sleeve (outer... Problem 2.5.12P: A circular, aluminum alloy bar of a length L = 1.8 m has a slot in the middle half of its length... Problem 2.5.13P: Rectangular bars of copper and aluminum are held by pins at their ends, as shown in the figure. Thin... Problem 2.5.14P: A brass sleeve S is fitted over a steel bolt B (see figure), and the nut is lightened until it is... Problem 2.5.15P: A rigid triangular frame is pivoted at C and held by two identical horizontal wires at points A and... Problem 2.5.16P: ,5-16 A rigid bar ABCD is pinned at end A and supported by two cables at points Band C (see figure).... Problem 2.5.17P: A copper bar AB with a length 25 in. and diameter 2 in. is placed in position at room temperature... Problem 2.5.18P: A steel wire AB is stretched between rigid supports (see figure). The initial priestess in the wire... Problem 2.5.19P: -19 The mechanical assembly shown in the figure consists of an aluminum tube, a rigid end plate, and... Problem 2.5.20P: A bar AB having a length L and axial rigidity EA is fixed at end A (see figure). At the other end, a... Problem 2.5.21P: Pipe 2 has been inserted snugly into Pipe I. but the holes Tor a connecting pin do not line up;... Problem 2.5.22P: A non prism elk- bar ABC made up of segments AB(length £,, cross-sectional area .Inland BC (length... Problem 2.5.23P: Wires B and C are attached to a support at the left-hand end and to a pin-supported rigid bar at the... Problem 2.5.24P: A rigid steel plate is supported by three posts of high-strength concrete each having an effective... Problem 2.5.25P: A capped cast-iron pipe is compressed by a brass rod, as shown. The mil is turned until it is just... Problem 2.5.26P: A plastic cylinder is held snugly between a rigid plate and. a foundation by two steel bolts (see... Problem 2.5.27P Problem 2.5.28P: Consider the sleeve made From two copper tubes joined by tin-lead solder over distance s. The sleeve... Problem 2.5.29P: A polyethylene tube (length L) has a cap that when installed compresses a spring (with under-formed... Problem 2.5.30P: Prestressed concrete beams are sometimes manufactured in the following manner. High-strength steel... Problem 2.5.31P Problem 2.6.1P: A steel bar of rectangular cross section (1.5 in. × 2.0 in.) Carries a tensile load P (see figure).... Problem 2.6.2P: A circular steel rod of diameter d is subjected to a tensile force P = 3.5 kN (see figure). The... Problem 2.6.3P: A standard brick (dimensions 8 in. × 4 in. × 2.5 in ) is compressed lengthwise by a force P. as... Problem 2.6.4P: A brass wire of diameter d = 2.42 mm is stretched tightly between rigid supports so that the tensile... Problem 2.6.5P Problem 2.6.6P: A steel bar with a diameter d = 12 mm is subjected to a tensile load P = 9.5 kN (see figure). (a)... Problem 2.6.7P: During a tension lest of a mild-steel specimen (see figure), the extensometer shows an elongation of... Problem 2.6.8P: A copper bar with a rectangular cross section is held without stress between rigid supports (see... Problem 2.6.9P: A prismatic bar with a length L = 3 ft and cross-sectional area A = 8 in2 is compressed by an axial... Problem 2.6.10P: A prismatic bar with a length L = 1 m and cross-sectional area A = 1200 mm2 is supported at the... Problem 2.6.11P: The plane truss in the figure is assembled From steel C 10 X 20 shapes (see Table 3(a) in Appendix... Problem 2.6.12P: Plastic bar of diameter d = 32 mm is compressed in a testing device by a Force P = 190 N that is... Problem 2.6.13P: A plastic bar of rectangular cross section (ft = 1.5 in. and h = 3 in.) fits snugly between rigid... Problem 2.6.14P: A copper bar of rectangular cross section (b = 18 mm and k = 40 mm) is held snugly (but without any... Problem 2.6.15P: A circular brass bar with a diameter J is member AC in truss ABC thai has load P = 5000 lb applied... Problem 2.6.16P: Two boards are joined by gluing along a scarf joint, as shown in the figure. For purposes of cutting... Problem 2.6.17P: Acting on the sides of a stress element cut from a bar in uniaxial stress are tensile stresses of... Problem 2.6.18P: A prismatic bar is subjected to an axial force that produces a tensile stress ????=65 MPa and a... Problem 2.6.19P: The normal stress on plane pq of a prismatic bar in tension (see figure) is found to be 7500 psi. On... Problem 2.6.20P: A tension member is to be constructed of two pieces or plastic glued along plane pq (see figure).... Problem 2.6.21P: -21 Plastic bar AB of rectangular cross section (6 = 0.75 in. and h = 1.5 in.) and length L = 2 Ft... Problem 2.6.22P: A compression bar having a square cross section with sides b = 50 mm is subjected to load P. The bar... Problem 2.7.1P: A prismatic bar AD of length L, cross-sectional area A. and modulus of elasticity E is subjected to... Problem 2.7.2P: A bar with a circular cross section having two different diameters d and 2d is shown in the figure.... Problem 2.7.3P: A three-story steel column in a building supports roof and floor loads as shown in the figure. The... Problem 2.7.4P: The bar ABC shown in the figure is loaded by a force P acting at end C and by a force Q acting at... Problem 2.7.5P: Determine the strain energy per unit volume (units of psi) and the strain energy per unit weight... Problem 2.7.6P: The truss ABC shown in the Figure is subjected to a horizontal load P at joint B. The two bars are... Problem 2.7.7P: -7 The truss A BC Shawn in the figure supports a horizontal load P1= 300 lb and a vertical load P2=... Problem 2.7.8P: The statically indeterminate structure shown in the figure consists of a horizontal rigid bar AB... Problem 2.7.9P: A slightly tapered bar AB of rectangular cross section and length L is acted upon by a force P (see... Problem 2.7.10P: A compressive load P is transmitted through a rigid plate to three magnesium-alloy bars that are... Problem 2.7.11P: A block B is pushed against three springs by a force P (see figure). The middle spring has a... Problem 2.7.12P: A bungee cord that behaves linearly elastically has an unstressed length L0= 760 mm and a stiffness... Problem 2.8.1P: A sliding collar of weight W = 150 lb falls From a height h = 2.0 in. onto a flange at the bottom of... Problem 2.8.2P: Solve the preceding problem if the collar has mass M = 80 kg, the height h = 0.5 m, the length L =... Problem 2.8.3P Problem 2.8.4P: A block weighing W = 5.0 N drops inside a cylinder from a height h = 200 mm onto a spring having... Problem 2.8.5P: Solve the preceding problem for W = 1.0 lb. h = 12 in.,and k =0.511,/in. Problem 2.8.6P Problem 2.8.7P: A weight W = 4500 lb falls from a height h onto a vertical wood pole having length L = 15 ft,... Problem 2.8.8P Problem 2.8.9P Problem 2.8.10P: A bumping post at the end of a track in a railway yard has a spring constant k = 8.0 MN/m (see... Problem 2.8.11P: A bumper for a mine car is constructed with a spring of stiffness k = 1120 lb/in. (see figure). If a... Problem 2.8.12P: A bungee jumper having a mass of 55 kg leaps from a bridge, braking her fall with a long elastic... Problem 2.8.13P Problem 2.8.14P: A rigid bar AB having a mass M = 1.0 kg and length L = 0.5 m is hinged at end A and supported at end... Problem 2.10.1P: The flat bars shown in parts a and b of the figure are subjected to tensile forces P = 3.0 kips.... Problem 2.10.2P: The flat bars shown in parts a and b of the figure are subjected to tensile forces P = 2.5 kN. Each... Problem 2.10.3P: A flat bar of width b and thickness t has a hole of diameter d drilled through it (see figure). The... Problem 2.10.4P: Around brass bar of a diameter d1= 20mm has upset ends each with a diameter d2= 26 mm (see figure).... Problem 2.10.5P Problem 2.10.6P: ,10-6 A prismatic bar with a diameter d0= 20 mm is being compared with a stepped bar of the same... Problem 2.10.7P: A stepped bar with a hole (see figure) has widths h = 2.4 in. and c = 1.6 in. The fillets have radii... Problem 2.11.1P: A bar AB of length L and weight density y hangs vertically under its awn weight (see figure). The... Problem 2.11.2P: A prismatic bar of length L = 1.8 m and cross-sectional area A = 480 mm" is loaded by forces P{= 30... Problem 2.11.3P Problem 2.11.4P: A prismatic bar in tension has a length L = 2.0 m and cross-sectional area A =249 mn2. The material... Problem 2.11.5P: An aluminum bar subjected to tensile Forces P has a length L = 150 in. and cross-sectional area A =... Problem 2.11.6P: A rigid bar AB is pinned al end A and is supported by a wine CD and loaded by a force P at end B... Problem 2.12.1P: Two identical bars AB and BC support a vertical load P (see figure). The bars are made of steel... Problem 2.12.2P: A stepped bar ACB with circular cross sections is held between rigid supports and loaded by an axial... Problem 2.12.3P: A horizontal rigid bar AB supporting a load P is hung from Five symmetrically placed wires, each of... Problem 2.12.4P Problem 2.12.5P: The symmetric truss ABCDE shown in the figure is constructed of four bars and supports a load P at... Problem 2.12.6P: Five bars, each having a diameter of 10 mm. support a load P as shown in the figure. Determine the... Problem 2.12.7P Problem 2.12.8P: A rigid bar ACB is supported on a fulcrum at C and loaded by a Force P at end B (see figure). Three... Problem 2.12.9P: The structure shown in the figure consists of a horizontal rigid bar ABCD supported by two steel... Problem 2.12.10P: Two cables, each having a length i. of approximately 40 m, support a loaded -container of weight W... Problem 2.12.11P: A hollow circular tube T of a length L = 15 in. is uniformly compressed by a force P acting through... format_list_bulleted

 Weight,
Weight, 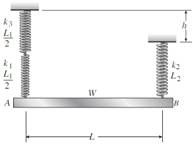 Weight,
Weight, 
 Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning
Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning