
Concept explainers
a.
To find: all zeros of the function.
a.
Answer to Problem 100CR
Explanation of Solution
Given information:
Concept used:-
Rational root test:- Let f(x) be a polynomial and c be constant term in f(x) and a is leading coefficient of f(x) then ratio of possible divisors of constant term and leading coefficient can rational zeros of function.
Rational root =
Calculation:- Possible divisors of constant term are
1stmethod:-
Since, we know zeros of a polynomial satisfies polynomial so, by putting these numbers in polynomial we can check which number is zero of polynomial.
2ndmethod: - using synthetic division method we can also check the roots of polynomial.
Now, we check, is (x+5) factor of
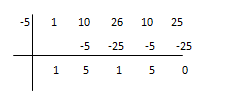
Hence, (x+ 5) is factor of
So,
Applying shreedhracharya for
So,
Therefore, (1) becomes
So, zeros of function are
b.
To represent: the polynomial as product of linear factor form.
b.
Answer to Problem 100CR
Explanation of Solution
Given information:
Zeros of given function are
Calculation:
From part (A) and equation (2), we have
c.
the x- intercept of function and verify it using graphing ultity.
c.
Answer to Problem 100CR
Explanation of Solution
Given information:
From part (B) we have
Concept used:-
The graph of polynomial cuts the x- axis at its real zeros.
Calculation:-
Since, we have
Real zeros of polynomial is -5.
So graph of given function will cut x-axis at x= -5
Verification:-
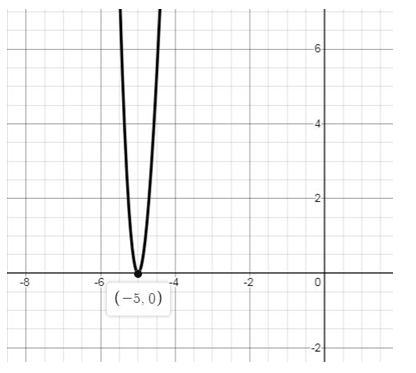
Using graph we can see graph of function cuts x-axis at x = -5.
Chapter 2 Solutions
PRECALCULUS W/LIMITS:GRAPH.APPROACH(HS)
- A fluid has density 800 kg/m³ and flows with velocity v = xi + yj + zk, where x, y, and z are measured in meters, and the components of u are measured in meters per second. Find the rate of flow outward through the part of the paraboloid z = 64 - x² - y² that lies above the xy plane.arrow_forward۳/۱ : +0 العنوان I need a detailed drawing with explanation R₂ = X2 2) slots per pole per phase 3/31 Le msl 180 60 Kd Ka Sin (1) Isin (6) sin(30) Sin (30) اذا ميريد شرح الكتب بس 0 بالفراغ 3) Cos (30) 0.866 4) Rotating 5) Synchronous speed, 120 x 50 S = 1000-950 1000 Copper bosses: 5kw Rotor input 5 6 : loo kw 6) 1 0.05 اذا ميريد شرح الكتب فقط 100 7) rotor DC 1000 ined sove in peaper I need a detailed solution on paper please // Find the solution of: |(2xy³ + 4x)y' = x²y² + y² 351 // Find the solution of: (1) 2xyy' = 1+ y² 01 175 T Τ Marrow_forwardFind the flux of the vector field F = (y,−x, 2²) through the helicoid with parameterization r(u, v) = (u cos v, u sin v, v) 0 ≤ u≤ 3, 0 ≤v≤ oriented away from the origin.arrow_forward
- 5. The graph of ƒ is given below. Sketch a graph of f'. 6. The graph of ƒ is given below. Sketch a graph of f'. 0 x 7. The graph of ƒ is given below. List the x-values where f is not differentiable. 0 A 2 4arrow_forward2. DRAW a picture, label using variables to represent each component, set up an equation to relate the variables, then differentiate the equation to solve the problem below. The top of a ladder slides down a vertical wall at a rate of 0.15 m/s. At the moment when the bottom of the ladder is 3 m from the wall, it slides away from the wall at a rate of 0.2 m/s. How long is the ladder?arrow_forwardPlease answer all questions and show full credit pleasearrow_forward
- please solve with full steps pleasearrow_forward4. Identify at least two mistakes in Francisco's work. Correct the mistakes and complete the problem by using the second derivative test. 2f 2X 2. Find the relative maximum and relative minimum points of f(x) = 2x3 + 3x² - 3, using the First Derivative Test or the Second Derivative Test. bx+ bx 6x +6x=0 12x- af 24 = 0 x=0 108 -2 5. Identify at least three mistakes in Francisco's work. Then sketch the graph of the function and label the local max and local min. 1. Find the equation of the tangent line to the curve y=x-2x3+x-2 at the point (1.-2). Sketch the araph of y=x42x3+x-2 and the tangent line at (1,-2) y' = 4x-6x y' (1) = 4(1) - 667 - 2 = 4(-2)4127-6(-2) 5-8-19-20 =arrow_forward۳/۱ R2X2 2) slots per pole per phase = 3/31 B=18060 msl Ka, Sin (1) Kdl Isin ( sin(30) Sin (30) اذا ميريد شرح الكتب بس 0 بالفراغ 3) Cos (30) 0.866 4) Rotating 120*50 5) Synchronous speed, 120 x 50 S1000-950 1000 Copper losses 5kw 50105 Rotor input 5 0.05 loo kw 6) 1 1000rpm اذا ميريد شرح الكتب فقط Look = 7) rotov DC ined sove in peaper PU + 96er Which of the following is converge, and which diverge? Give reasons for your answers with details. When your answer then determine the convergence sum if possible. 3" 6" Σ=1 (2-1) π X9arrow_forward
- 1 R2 X2 2) slots per pole per phase = 3/31 B = 180 - 60 msl Kd Kol, Sin (no) Isin (6) 2 sin(30) Sin (30) اذا ميريد شرح الكتب بس 0 بالفراغ 3) Cos (30) 0.866 4) Rotating 5) Synchronous speed; 120*50 Looo rem G S = 1000-950 solos 1000 Copper losses: 5kw Rotor input: 5 loo kw 0.05 1 اذا میرید شرح الكتب فقط look 7) rotor DC ined sove in pea PU+96er Q2// Find the volume of the solid bounded above by the cynnuer 2=6-x², on the sides by the cylinder x² + y² = 9, and below by the xy-plane. Q041 Convert 2 2x-2 Lake Gex 35 w2x-xབོ ,4-ཙཱཔ-y √4-x²-yz 21xy²dzdydx to(a) cylindrical coordinates, (b) Spherical coordinates. 201 25arrow_forwardshow full work pleasearrow_forward3. Describe the steps you would take to find the absolute max of the following function using Calculus f(x) = : , [-1,2]. Then use a graphing calculator to x-1 x²-x+1 approximate the absolute max in the closed interval.arrow_forward
 Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning
Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON
Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
 Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning
Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning





