
Concept explainers
a.
Describe similarity and difference among the graphs.
a.
Answer to Problem 97E
The function is odd as function is symmetric with respect to origin.
Explanation of Solution
Calculation:
Let us plot the graph of following function:
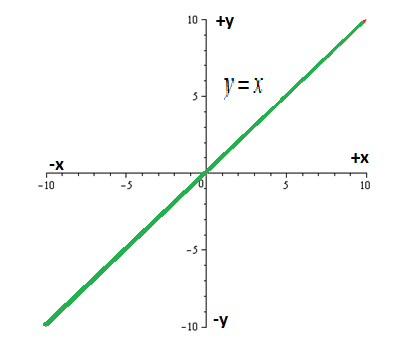
A function
Hence, the function is odd as function is symmetric with respect to origin.
b.
Describe similarity and difference among the graphs.
b.
Answer to Problem 97E
The function is even as function is symmetric with respect to
Explanation of Solution
Calculation:
Let us plot the graph of following function:
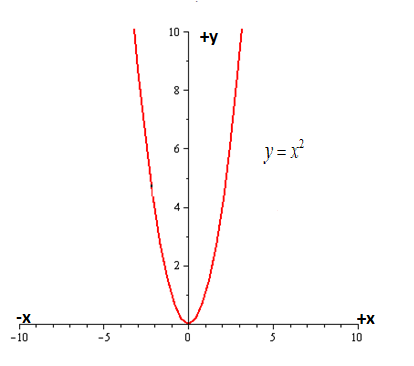
A function
Hence, the function is even as function is symmetric with respect to
c.
Describe similarity and difference among the graphs.
c.
Answer to Problem 97E
The function is odd as function is symmetric with respect to origin
Explanation of Solution
Calculation:
Let us plot the graph of following function:
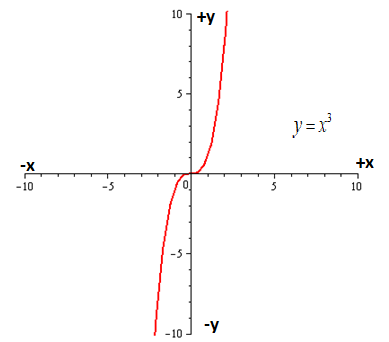
A function
Hence, the function is odd as function is symmetric with respect to origin.
d.
Describe similarity and difference among the graphs.
d.
Answer to Problem 97E
The function is even as function is symmetric with respect to
Explanation of Solution
Calculation:
Let us plot the graph of following function:
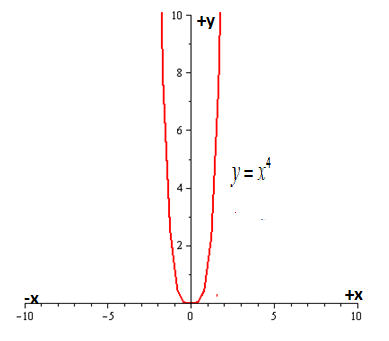
A function
Hence, the function is even as function is symmetric with respect to
e.
Describe similarity and difference among the graphs.
e.
Answer to Problem 97E
The function is odd as function is symmetric with respect to origin.
Explanation of Solution
Calculation:
Let us plot the graph of following function:
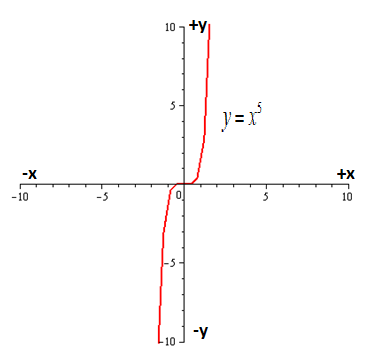
A function
The function is odd as function is symmetric with respect to origin.
f.
Describe similarity and difference among the graphs.
f.
Answer to Problem 97E
The graphs of even functions are symmetric with respect to
Explanation of Solution
Calculation:
Let us plot the graph of following function:
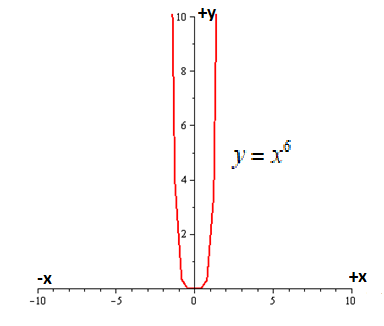
A function
The function is odd as function is symmetric with respect to
The function with even power of is even functions and with odd power of is odd function.
Hence, The functions
Chapter 1 Solutions
EBK PRECALCULUS W/LIMITS
- what is the horizonal asymptote of question d?arrow_forward2 3 Polar axis The graph of the polar function r = = f(0) is given in the polar coordinate system. Which of the following defines f(0) for 0 ≤ 0 ≤ 2πT? A 3+ cos(30) B 3 cos(30) C 3+ sin(30) D 3 sin (30)arrow_forwardSolve by superposition method the following DE: y^(4) - y = xe^(x) sen(2x), conditions: y(0) = y'(0) = y''(0) = y'''(0) =0arrow_forward
- Use the annulus method to find the solution of the DE: y''' + 8y = e^(3x) sen(3x) cos(3x)arrow_forward3:59 m s ☑ D'Aniello Boutique | Fashion VOLTE danielloboutique.it/asia SUBSCRIBE NOW: 10% OFF TO USE ANYTIME YOU WANT d'aniello NEW IN WOMEN NEW IN MEN WINTER SALE: 50% OFF on FW24 SHOP WOMEN SHOP MENarrow_forwardJOB UPDATE EMERSON GRAD ENGINEER (FRESHERS) SOFTWARE ENGG NEW RELIC BROWSERSTACK (FRESHERS) SOFTWARE ENGG FULL STACK DATA ENGINEER GENPACT + PYTHON CARS24 WORK FROM HOME #vinkjobs TELE PERFORMANCE Vinkjobs.com CUSTOMER SUPPORT Search "Vinkjobs.com" on Googlearrow_forward
- do question 2 pleasearrow_forwardquestion 10 pleasearrow_forward00 (a) Starting with the geometric series Σ X^, find the sum of the series n = 0 00 Σηχη - 1, |x| < 1. n = 1 (b) Find the sum of each of the following series. 00 Σnx", n = 1 |x| < 1 (ii) n = 1 sin (c) Find the sum of each of the following series. (i) 00 Σn(n-1)x^, |x| <1 n = 2 (ii) 00 n = 2 n² - n 4n (iii) M8 n = 1 շոarrow_forward
- (a) Use differentiation to find a power series representation for 1 f(x) = (4 + x)²* f(x) = 00 Σ n = 0 What is the radius of convergence, R? R = (b) Use part (a) to find a power series for f(x) = 1 (4 + x)³° f(x) = 00 Σ n = 0 What is the radius of convergence, R? R = (c) Use part (b) to find a power series for f(x) = x² (4 + x)³* 00 f(x) = Σ n = 2 What is the radius of convergence, R? R = Need Help? Read It Watch It SUBMIT ANSWERarrow_forwardanswer for question 4 pleasearrow_forward(3) (20 points) Let F(x, y, z) = (y, z, x²z). Define E = {(x, y, z) | x² + y² ≤ z ≤ 1, x ≤ 0}. (a) (2 points) Calculate the divergence V. F. (b) (4 points) Let D = {(x, y) | x² + y² ≤ 1, x ≤ 0} Without calculation, show that the triple integral √ (V · F) dV = √ 2²(1. = x²(1 − x² - y²) dA. Earrow_forward
 Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning
Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON
Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
 Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning
Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning





