
Concept explainers
(a)
To find:The function that represent the situation of the given equation.
(a)
Answer to Problem 67E
The function that represent the situation of the given equation is
Explanation of Solution
Given information:
The given equationis
The height is
The initial velocity is
Calculation:
Using the position
The function is.
Therefore, the function that represent the situation of the given equation is
(b)
To graph: For the given function.
(b)
Explanation of Solution
Given information:
The given function is
Graph:
The graph for the given function is shown in figure (1).
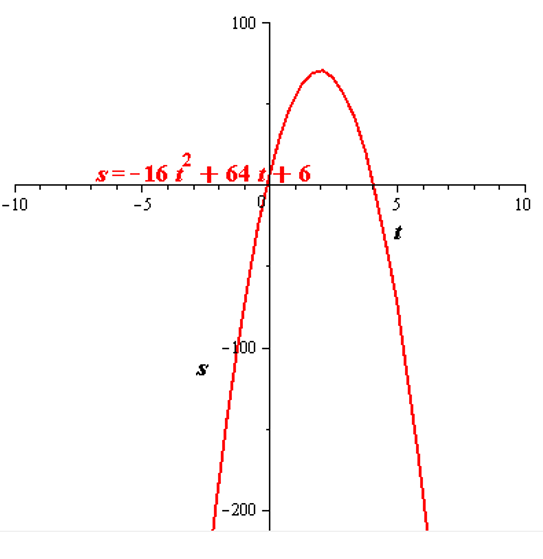
Figure (1)
Interpretation: Graph for the function
(c)
To find: The average rate of change of the function from
(c)
Answer to Problem 67E
The average rate of change of the function from
Explanation of Solution
Given information:
The given equation is
The values are
Calculation:
Average rate of change of the function from
Calculate the values at
Calculate average rate of change of the function from
Therefore, the average rate of change of the function from
(d)
To find: The behavior of slope of the secant line through
(d)
Answer to Problem 67E
The slope of the secant line through
Explanation of Solution
Given information:
The given equation is
The values are
Calculation:
The average rate of change between any two points
Therefore, the slope of the secant line through
(e)
To find: The slope of the secant line through
(e)
Answer to Problem 67E
The slope of the secant line through
Explanation of Solution
Given information:
The given equation is
The values are
Calculation:
Using the above value.
The equation of secant line is.
Therefore, the slope of the secant line through
(f)
To graph: For the secant line.
(f)
Explanation of Solution
Given information:
The secant line is
Graph:
The graph for the secant line is shown in figure (1).
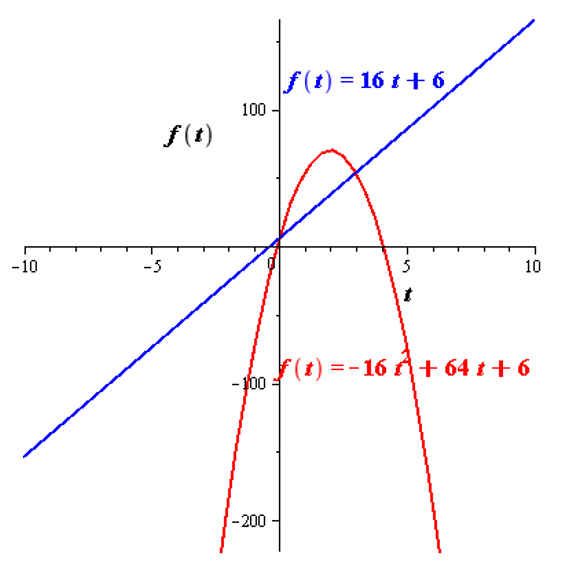
Figure (1)
Interpretation: Graph for the secant line
Chapter 1 Solutions
EBK PRECALCULUS W/LIMITS
- 8. For x>_1, the continuous function g is decreasing and positive. A portion of the graph of g is shown above. For n>_1, the nth term of the series summation from n=1 to infinity a_n is defined by a_n=g(n). If intergral 1 to infinity g(x)dx converges to 8, which of the following could be true? A) summation n=1 to infinity a_n = 6. B) summation n=1 to infinity a_n =8. C) summation n=1 to infinity a_n = 10. D) summation n=1 to infinity a_n diverges.arrow_forwardPLEASE SHOW ME THE RIGHT ANSWER/SOLUTION SHOW ME ALL THE NEDDED STEP 13: If the perimeter of a square is shrinking at a rate of 8 inches per second, find the rate at which its area is changing when its area is 25 square inches.arrow_forwardDO NOT GIVE THE WRONG ANSWER SHOW ME ALL THE NEEDED STEPS 11: A rectangle has a base that is growing at a rate of 3 inches per second and a height that is shrinking at a rate of one inch per second. When the base is 12 inches and the height is 5 inches, at what rate is the area of the rectangle changing?arrow_forward
- please answer by showing all the dfalowing necessary step DO NOT GIVE ME THE WRONG ANSWER The sides of a cube of ice are melting at a rate of 1 inch per hour. When its volume is 64 cubic inches, at what rate is its volume changing?arrow_forwardSox & Sin (px) dx 0arrow_forward8 L 8 e ipx dxarrow_forward
- Find the Taylor polynomial T³(×) for the function f centered at the number a. f(x) = xe-2x a = 0 T3(x) =arrow_forwardFor each graph in Figure 16, determine whether f (1) is larger or smaller than the slope of the secant line between x = 1 and x = 1 + h for h > 0. Explain your reasoningarrow_forwardPoints z1 and z2 are shown on the graph.z1 is at (4 real,6 imaginary), z2 is at (-5 real, 2 imaginary)Part A: Identify the points in standard form and find the distance between them.Part B: Give the complex conjugate of z2 and explain how to find it geometrically.Part C: Find z2 − z1 geometrically and explain your steps.arrow_forward
- A polar curve is represented by the equation r1 = 7 + 4cos θ.Part A: What type of limaçon is this curve? Justify your answer using the constants in the equation.Part B: Is the curve symmetrical to the polar axis or the line θ = pi/2 Justify your answer algebraically.Part C: What are the two main differences between the graphs of r1 = 7 + 4cos θ and r2 = 4 + 4cos θ?arrow_forwardA curve, described by x2 + y2 + 8x = 0, has a point A at (−4, 4) on the curve.Part A: What are the polar coordinates of A? Give an exact answer.Part B: What is the polar form of the equation? What type of polar curve is this?Part C: What is the directed distance when Ø = 5pi/6 Give an exact answer.arrow_forwardNew folder 10. Find the area enclosed by the loop of the curve (1- t², t-t³)arrow_forward
 Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning
Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON
Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
 Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning
Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning





