EBK PRECALCULUS W/LIMITS
4th Edition
ISBN: 9781337516853
Author: Larson
Publisher: CENGAGE CO
expand_more
expand_more
format_list_bulleted
Videos
Question
Chapter 1.7, Problem 27E
(a)
To determine
To identify: the parent function f(x) of g(x)
(a)
Expert Solution
Explanation of Solution
Given information:
Consider g(x)=|x−1|+2
Parent function is the simplest function of family of functions, which has the same shape as that of entire family.
We have g(x)=|x−1|+2
The function f(x)=|x| is the simplest function and have same shape as that of
g(x).
Hence, the parent function is f(x)=|x| .
(b)
To determine
To explain: the sequence of transformations from f(x) to g(x).
(b)
Expert Solution
Explanation of Solution
Given information:
Consider g(x)=|x−1|+2
The parent function is f(x)=|x| .
If The function f(x)=|x| is right shift one unit and vertical up shift two units, then
g(x)=|x−1|+2 is obtained.
Hence, the transformation of f to g is “ right shift 1 unit up shift 2 units”.
(c)
To determine
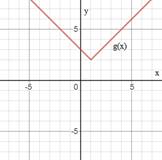
To sketch: the graph of g(x)
(c)
Expert Solution
Explanation of Solution
Given information:
Consider g(x)=|x−1|+2
Graph:
The graph of g(x)=|x−1|+2
(d)
To determine
To write: the function g(x) in terms of f(x)
(d)
Expert Solution
Explanation of Solution
Given information:
Consider g(x)=|x−1|+2
Parent function is f(x)=|x|
We have
g(x)=|x−1|+2=f(x−1)+2
Hence, the parent function is g(x)=f(x−1)+2 .
Chapter 1 Solutions
EBK PRECALCULUS W/LIMITS
Ch. 1.1 - Prob. 1ECh. 1.1 - Prob. 2ECh. 1.1 - Prob. 3ECh. 1.1 - Prob. 4ECh. 1.1 - Prob. 5ECh. 1.1 - Prob. 6ECh. 1.1 - Prob. 7ECh. 1.1 - Prob. 8ECh. 1.1 - Prob. 9ECh. 1.1 - Prob. 10E
Ch. 1.1 - Prob. 11ECh. 1.1 - Prob. 12ECh. 1.1 - Prob. 13ECh. 1.1 - Prob. 14ECh. 1.1 - Prob. 15ECh. 1.1 - Prob. 16ECh. 1.1 - Prob. 17ECh. 1.1 - Prob. 18ECh. 1.1 - Prob. 19ECh. 1.1 - Prob. 20ECh. 1.1 - Prob. 21ECh. 1.1 - Prob. 22ECh. 1.1 - Prob. 23ECh. 1.1 - Prob. 24ECh. 1.1 - Prob. 25ECh. 1.1 - Prob. 26ECh. 1.1 - Prob. 27ECh. 1.1 - Prob. 28ECh. 1.1 - Prob. 29ECh. 1.1 - Prob. 30ECh. 1.1 - Prob. 31ECh. 1.1 - Prob. 32ECh. 1.1 - Prob. 33ECh. 1.1 - Prob. 34ECh. 1.1 - Prob. 35ECh. 1.1 - Prob. 36ECh. 1.1 - Prob. 37ECh. 1.1 - Prob. 38ECh. 1.1 - Prob. 39ECh. 1.1 - Prob. 40ECh. 1.1 - Prob. 41ECh. 1.1 - Prob. 42ECh. 1.1 - Prob. 43ECh. 1.1 - Prob. 44ECh. 1.1 - Prob. 45ECh. 1.1 - Prob. 46ECh. 1.1 - Prob. 47ECh. 1.1 - Prob. 48ECh. 1.1 - Prob. 49ECh. 1.1 - Prob. 50ECh. 1.1 - Prob. 51ECh. 1.1 - Prob. 52ECh. 1.1 - Prob. 53ECh. 1.1 - Prob. 54ECh. 1.1 - Prob. 55ECh. 1.1 - Prob. 56ECh. 1.1 - Prob. 57ECh. 1.1 - Prob. 58ECh. 1.1 - Prob. 59ECh. 1.1 - Prob. 60ECh. 1.2 - Prob. 1ECh. 1.2 - Prob. 2ECh. 1.2 - Prob. 3ECh. 1.2 - Prob. 4ECh. 1.2 - Prob. 5ECh. 1.2 - Prob. 6ECh. 1.2 - Prob. 7ECh. 1.2 - Prob. 8ECh. 1.2 - Prob. 9ECh. 1.2 - Prob. 10ECh. 1.2 - Prob. 11ECh. 1.2 - Prob. 12ECh. 1.2 - Prob. 13ECh. 1.2 - Prob. 14ECh. 1.2 - Prob. 15ECh. 1.2 - Prob. 16ECh. 1.2 - Prob. 17ECh. 1.2 - Prob. 18ECh. 1.2 - Prob. 19ECh. 1.2 - Prob. 20ECh. 1.2 - Prob. 21ECh. 1.2 - Prob. 22ECh. 1.2 - Prob. 23ECh. 1.2 - Prob. 24ECh. 1.2 - Prob. 25ECh. 1.2 - Prob. 26ECh. 1.2 - Prob. 27ECh. 1.2 - Prob. 28ECh. 1.2 - Prob. 29ECh. 1.2 - Prob. 30ECh. 1.2 - Prob. 31ECh. 1.2 - Prob. 32ECh. 1.2 - Prob. 33ECh. 1.2 - Prob. 34ECh. 1.2 - Prob. 35ECh. 1.2 - Prob. 36ECh. 1.2 - Prob. 37ECh. 1.2 - Prob. 38ECh. 1.2 - Prob. 39ECh. 1.2 - Prob. 40ECh. 1.2 - Prob. 41ECh. 1.2 - Prob. 42ECh. 1.2 - Prob. 43ECh. 1.2 - Prob. 44ECh. 1.2 - Prob. 45ECh. 1.2 - Prob. 46ECh. 1.2 - Prob. 47ECh. 1.2 - Prob. 48ECh. 1.2 - Prob. 49ECh. 1.2 - Prob. 50ECh. 1.2 - Prob. 51ECh. 1.2 - Prob. 52ECh. 1.2 - Prob. 53ECh. 1.2 - Prob. 54ECh. 1.2 - Prob. 55ECh. 1.2 - Prob. 56ECh. 1.2 - Prob. 57ECh. 1.2 - Prob. 58ECh. 1.2 - Prob. 59ECh. 1.2 - Prob. 60ECh. 1.2 - Prob. 61ECh. 1.2 - Prob. 62ECh. 1.2 - Prob. 63ECh. 1.2 - Prob. 64ECh. 1.2 - Prob. 65ECh. 1.2 - Prob. 66ECh. 1.2 - Prob. 67ECh. 1.2 - Prob. 68ECh. 1.2 - Prob. 69ECh. 1.2 - Prob. 70ECh. 1.2 - Prob. 71ECh. 1.2 - Prob. 72ECh. 1.2 - Prob. 73ECh. 1.2 - Prob. 74ECh. 1.2 - Prob. 75ECh. 1.2 - Prob. 76ECh. 1.2 - Prob. 77ECh. 1.2 - Prob. 78ECh. 1.2 - Prob. 79ECh. 1.2 - Prob. 80ECh. 1.2 - Prob. 81ECh. 1.2 - Prob. 82ECh. 1.2 - Prob. 83ECh. 1.2 - Prob. 84ECh. 1.2 - Prob. 85ECh. 1.2 - Prob. 86ECh. 1.2 - Prob. 87ECh. 1.2 - Prob. 88ECh. 1.2 - Prob. 89ECh. 1.2 - Prob. 90ECh. 1.2 - Prob. 91ECh. 1.3 - Prob. 1ECh. 1.3 - Prob. 2ECh. 1.3 - Prob. 3ECh. 1.3 - Prob. 4ECh. 1.3 - Prob. 5ECh. 1.3 - Prob. 6ECh. 1.3 - Prob. 7ECh. 1.3 - Prob. 8ECh. 1.3 - Prob. 9ECh. 1.3 - Prob. 10ECh. 1.3 - Prob. 11ECh. 1.3 - Prob. 12ECh. 1.3 - Prob. 13ECh. 1.3 - Prob. 14ECh. 1.3 - Prob. 15ECh. 1.3 - Prob. 16ECh. 1.3 - Prob. 17ECh. 1.3 - Prob. 18ECh. 1.3 - Prob. 19ECh. 1.3 - Prob. 20ECh. 1.3 - Prob. 21ECh. 1.3 - Prob. 22ECh. 1.3 - Prob. 23ECh. 1.3 - Prob. 24ECh. 1.3 - Prob. 25ECh. 1.3 - Prob. 26ECh. 1.3 - Prob. 27ECh. 1.3 - Prob. 28ECh. 1.3 - Prob. 29ECh. 1.3 - Prob. 30ECh. 1.3 - Prob. 31ECh. 1.3 - Prob. 32ECh. 1.3 - Prob. 33ECh. 1.3 - Prob. 34ECh. 1.3 - Prob. 35ECh. 1.3 - Prob. 36ECh. 1.3 - Prob. 37ECh. 1.3 - Prob. 38ECh. 1.3 - Prob. 39ECh. 1.3 - Prob. 40ECh. 1.3 - Prob. 41ECh. 1.3 - Prob. 42ECh. 1.3 - Prob. 43ECh. 1.3 - Prob. 44ECh. 1.3 - Prob. 45ECh. 1.3 - Prob. 46ECh. 1.3 - Prob. 47ECh. 1.3 - Prob. 48ECh. 1.3 - Prob. 49ECh. 1.3 - Prob. 50ECh. 1.3 - Prob. 51ECh. 1.3 - Prob. 52ECh. 1.3 - Prob. 53ECh. 1.3 - Prob. 54ECh. 1.3 - Prob. 55ECh. 1.3 - Prob. 56ECh. 1.3 - Prob. 57ECh. 1.3 - Prob. 58ECh. 1.3 - Prob. 59ECh. 1.3 - Prob. 60ECh. 1.3 - Prob. 61ECh. 1.3 - Prob. 62ECh. 1.3 - Prob. 63ECh. 1.3 - Prob. 64ECh. 1.3 - Prob. 65ECh. 1.3 - Prob. 66ECh. 1.3 - Prob. 67ECh. 1.3 - Prob. 68ECh. 1.3 - Prob. 69ECh. 1.3 - Prob. 70ECh. 1.3 - Prob. 71ECh. 1.3 - Prob. 72ECh. 1.3 - Prob. 73ECh. 1.3 - Prob. 74ECh. 1.3 - Prob. 75ECh. 1.3 - Prob. 76ECh. 1.3 - Prob. 77ECh. 1.3 - Prob. 78ECh. 1.3 - Prob. 79ECh. 1.3 - Prob. 80ECh. 1.3 - Prob. 81ECh. 1.3 - Prob. 82ECh. 1.3 - Prob. 83ECh. 1.3 - Prob. 84ECh. 1.3 - Prob. 85ECh. 1.3 - Prob. 86ECh. 1.3 - Prob. 87ECh. 1.3 - Prob. 88ECh. 1.3 - Prob. 89ECh. 1.3 - Prob. 90ECh. 1.3 - Prob. 91ECh. 1.3 - Prob. 92ECh. 1.3 - Prob. 93ECh. 1.3 - Prob. 94ECh. 1.3 - Prob. 95ECh. 1.3 - Prob. 96ECh. 1.3 - Prob. 97ECh. 1.3 - Prob. 98ECh. 1.3 - Prob. 99ECh. 1.3 - Prob. 100ECh. 1.3 - Prob. 101ECh. 1.3 - Prob. 102ECh. 1.3 - Prob. 103ECh. 1.3 - Prob. 104ECh. 1.3 - Prob. 105ECh. 1.3 - Prob. 106ECh. 1.3 - Prob. 107ECh. 1.3 - Prob. 108ECh. 1.3 - Prob. 109ECh. 1.3 - Prob. 110ECh. 1.3 - Prob. 111ECh. 1.3 - Prob. 112ECh. 1.3 - Prob. 113ECh. 1.3 - Prob. 114ECh. 1.4 - Prob. 1ECh. 1.4 - Prob. 2ECh. 1.4 - Prob. 3ECh. 1.4 - Prob. 4ECh. 1.4 - Prob. 5ECh. 1.4 - Prob. 6ECh. 1.4 - Prob. 7ECh. 1.4 - Prob. 8ECh. 1.4 - Prob. 9ECh. 1.4 - Prob. 10ECh. 1.4 - Prob. 11ECh. 1.4 - Prob. 12ECh. 1.4 - Prob. 13ECh. 1.4 - Prob. 14ECh. 1.4 - Prob. 15ECh. 1.4 - Prob. 16ECh. 1.4 - Prob. 17ECh. 1.4 - Prob. 18ECh. 1.4 - Prob. 19ECh. 1.4 - Prob. 20ECh. 1.4 - Prob. 21ECh. 1.4 - Prob. 22ECh. 1.4 - Prob. 23ECh. 1.4 - Prob. 24ECh. 1.4 - Prob. 25ECh. 1.4 - Prob. 26ECh. 1.4 - Prob. 27ECh. 1.4 - Prob. 28ECh. 1.4 - Prob. 29ECh. 1.4 - Prob. 30ECh. 1.4 - Prob. 31ECh. 1.4 - Prob. 32ECh. 1.4 - Prob. 33ECh. 1.4 - Prob. 34ECh. 1.4 - Prob. 35ECh. 1.4 - Prob. 36ECh. 1.4 - Prob. 37ECh. 1.4 - Prob. 38ECh. 1.4 - Prob. 39ECh. 1.4 - Prob. 40ECh. 1.4 - Prob. 41ECh. 1.4 - Prob. 42ECh. 1.4 - Prob. 43ECh. 1.4 - Prob. 44ECh. 1.4 - Prob. 45ECh. 1.4 - Prob. 46ECh. 1.4 - Prob. 47ECh. 1.4 - Prob. 48ECh. 1.4 - Prob. 49ECh. 1.4 - Prob. 50ECh. 1.4 - Prob. 51ECh. 1.4 - Prob. 52ECh. 1.4 - Prob. 53ECh. 1.4 - Prob. 54ECh. 1.4 - Prob. 55ECh. 1.4 - Prob. 56ECh. 1.4 - Prob. 57ECh. 1.4 - Prob. 58ECh. 1.4 - Prob. 59ECh. 1.4 - Prob. 60ECh. 1.4 - Prob. 61ECh. 1.4 - Prob. 62ECh. 1.4 - Prob. 63ECh. 1.4 - Prob. 64ECh. 1.4 - Prob. 65ECh. 1.4 - Prob. 66ECh. 1.4 - Prob. 67ECh. 1.4 - Prob. 68ECh. 1.4 - Prob. 69ECh. 1.4 - Prob. 70ECh. 1.4 - Prob. 71ECh. 1.4 - Prob. 72ECh. 1.4 - Prob. 73ECh. 1.4 - Prob. 74ECh. 1.4 - Prob. 75ECh. 1.4 - Prob. 76ECh. 1.4 - Prob. 77ECh. 1.4 - Prob. 78ECh. 1.4 - Prob. 79ECh. 1.4 - Prob. 80ECh. 1.4 - Prob. 81ECh. 1.4 - Prob. 82ECh. 1.4 - Prob. 83ECh. 1.4 - Prob. 84ECh. 1.4 - Prob. 85ECh. 1.4 - Prob. 86ECh. 1.4 - Prob. 87ECh. 1.4 - Prob. 88ECh. 1.4 - Prob. 89ECh. 1.4 - Prob. 90ECh. 1.4 - Prob. 91ECh. 1.4 - Prob. 92ECh. 1.4 - Prob. 93ECh. 1.4 - Prob. 94ECh. 1.5 - Prob. 1ECh. 1.5 - Prob. 2ECh. 1.5 - Prob. 3ECh. 1.5 - Prob. 4ECh. 1.5 - Prob. 5ECh. 1.5 - Prob. 6ECh. 1.5 - Prob. 7ECh. 1.5 - Prob. 8ECh. 1.5 - Prob. 9ECh. 1.5 - Prob. 10ECh. 1.5 - Prob. 11ECh. 1.5 - Prob. 12ECh. 1.5 - Prob. 13ECh. 1.5 - Prob. 14ECh. 1.5 - Prob. 15ECh. 1.5 - Prob. 16ECh. 1.5 - Prob. 17ECh. 1.5 - Prob. 18ECh. 1.5 - Prob. 19ECh. 1.5 - Prob. 20ECh. 1.5 - Prob. 21ECh. 1.5 - Prob. 22ECh. 1.5 - Prob. 23ECh. 1.5 - Prob. 24ECh. 1.5 - Prob. 25ECh. 1.5 - Prob. 26ECh. 1.5 - Prob. 27ECh. 1.5 - Prob. 28ECh. 1.5 - Prob. 29ECh. 1.5 - Prob. 30ECh. 1.5 - Prob. 31ECh. 1.5 - Prob. 32ECh. 1.5 - Prob. 33ECh. 1.5 - Prob. 34ECh. 1.5 - Prob. 35ECh. 1.5 - Prob. 36ECh. 1.5 - Prob. 37ECh. 1.5 - Prob. 38ECh. 1.5 - Prob. 39ECh. 1.5 - Prob. 40ECh. 1.5 - Prob. 41ECh. 1.5 - Prob. 42ECh. 1.5 - Prob. 43ECh. 1.5 - Prob. 44ECh. 1.5 - Prob. 45ECh. 1.5 - Prob. 46ECh. 1.5 - Prob. 47ECh. 1.5 - Prob. 48ECh. 1.5 - Prob. 49ECh. 1.5 - Prob. 50ECh. 1.5 - Prob. 51ECh. 1.5 - Prob. 52ECh. 1.5 - Prob. 53ECh. 1.5 - Prob. 54ECh. 1.5 - Prob. 55ECh. 1.5 - Prob. 56ECh. 1.5 - Prob. 57ECh. 1.5 - Prob. 58ECh. 1.5 - Prob. 59ECh. 1.5 - Prob. 60ECh. 1.5 - Prob. 61ECh. 1.5 - Prob. 62ECh. 1.5 - Prob. 63ECh. 1.5 - Prob. 64ECh. 1.5 - Prob. 65ECh. 1.5 - Prob. 66ECh. 1.5 - Prob. 67ECh. 1.5 - Prob. 68ECh. 1.5 - Prob. 69ECh. 1.5 - Prob. 70ECh. 1.5 - Prob. 71ECh. 1.5 - Prob. 72ECh. 1.5 - Prob. 73ECh. 1.5 - Prob. 74ECh. 1.5 - Prob. 75ECh. 1.5 - Prob. 76ECh. 1.5 - Prob. 77ECh. 1.5 - Prob. 78ECh. 1.5 - Prob. 79ECh. 1.5 - Prob. 80ECh. 1.5 - Prob. 81ECh. 1.5 - Prob. 82ECh. 1.5 - Prob. 83ECh. 1.5 - Prob. 84ECh. 1.5 - Prob. 85ECh. 1.5 - Prob. 86ECh. 1.5 - Prob. 87ECh. 1.5 - Prob. 88ECh. 1.5 - Prob. 89ECh. 1.5 - Prob. 90ECh. 1.5 - Prob. 91ECh. 1.5 - Prob. 92ECh. 1.5 - Prob. 93ECh. 1.5 - Prob. 94ECh. 1.5 - Prob. 95ECh. 1.5 - Prob. 96ECh. 1.5 - Prob. 97ECh. 1.5 - Prob. 98ECh. 1.5 - Prob. 99ECh. 1.6 - Prob. 1ECh. 1.6 - Prob. 2ECh. 1.6 - Prob. 3ECh. 1.6 - Prob. 4ECh. 1.6 - Prob. 5ECh. 1.6 - Prob. 6ECh. 1.6 - Prob. 7ECh. 1.6 - Prob. 8ECh. 1.6 - Prob. 9ECh. 1.6 - Prob. 10ECh. 1.6 - Prob. 11ECh. 1.6 - Prob. 12ECh. 1.6 - Prob. 13ECh. 1.6 - Prob. 14ECh. 1.6 - Prob. 15ECh. 1.6 - Prob. 16ECh. 1.6 - Prob. 17ECh. 1.6 - Prob. 18ECh. 1.6 - Prob. 19ECh. 1.6 - Prob. 20ECh. 1.6 - Prob. 21ECh. 1.6 - Prob. 22ECh. 1.6 - Prob. 23ECh. 1.6 - Prob. 24ECh. 1.6 - Prob. 25ECh. 1.6 - Prob. 26ECh. 1.6 - Prob. 27ECh. 1.6 - Prob. 28ECh. 1.6 - Prob. 29ECh. 1.6 - Prob. 30ECh. 1.6 - Prob. 31ECh. 1.6 - Prob. 32ECh. 1.6 - Prob. 33ECh. 1.6 - Prob. 34ECh. 1.6 - Prob. 35ECh. 1.6 - Prob. 36ECh. 1.6 - Prob. 37ECh. 1.6 - Prob. 38ECh. 1.6 - Prob. 39ECh. 1.6 - Prob. 40ECh. 1.6 - Prob. 41ECh. 1.6 - Prob. 42ECh. 1.6 - Prob. 43ECh. 1.6 - Prob. 44ECh. 1.6 - Prob. 45ECh. 1.6 - Prob. 46ECh. 1.6 - Prob. 47ECh. 1.6 - Prob. 48ECh. 1.6 - Prob. 49ECh. 1.6 - Prob. 50ECh. 1.7 - Prob. 1ECh. 1.7 - Prob. 2ECh. 1.7 - Prob. 3ECh. 1.7 - Prob. 4ECh. 1.7 - Prob. 5ECh. 1.7 - Prob. 6ECh. 1.7 - Prob. 7ECh. 1.7 - Prob. 8ECh. 1.7 - Prob. 9ECh. 1.7 - Prob. 10ECh. 1.7 - Prob. 11ECh. 1.7 - Prob. 12ECh. 1.7 - Prob. 13ECh. 1.7 - Prob. 14ECh. 1.7 - Prob. 15ECh. 1.7 - Prob. 16ECh. 1.7 - Prob. 17ECh. 1.7 - Prob. 18ECh. 1.7 - Prob. 19ECh. 1.7 - Prob. 20ECh. 1.7 - Prob. 21ECh. 1.7 - Prob. 22ECh. 1.7 - Prob. 23ECh. 1.7 - Prob. 24ECh. 1.7 - Prob. 25ECh. 1.7 - Prob. 26ECh. 1.7 - Prob. 27ECh. 1.7 - Prob. 28ECh. 1.7 - Prob. 29ECh. 1.7 - Prob. 30ECh. 1.7 - Prob. 31ECh. 1.7 - Prob. 32ECh. 1.7 - Prob. 33ECh. 1.7 - Prob. 34ECh. 1.7 - Prob. 35ECh. 1.7 - Prob. 36ECh. 1.7 - Prob. 37ECh. 1.7 - Prob. 38ECh. 1.7 - Prob. 39ECh. 1.7 - Prob. 40ECh. 1.7 - Prob. 41ECh. 1.7 - Prob. 42ECh. 1.7 - Prob. 43ECh. 1.7 - Prob. 44ECh. 1.7 - Prob. 45ECh. 1.7 - Prob. 46ECh. 1.7 - Prob. 47ECh. 1.7 - Prob. 48ECh. 1.7 - Prob. 49ECh. 1.7 - Prob. 50ECh. 1.7 - Prob. 51ECh. 1.7 - Prob. 52ECh. 1.7 - Prob. 53ECh. 1.7 - Prob. 54ECh. 1.7 - Prob. 55ECh. 1.7 - Prob. 56ECh. 1.7 - Prob. 57ECh. 1.7 - Prob. 58ECh. 1.7 - Prob. 59ECh. 1.7 - Prob. 60ECh. 1.7 - Prob. 61ECh. 1.7 - Prob. 62ECh. 1.7 - Prob. 63ECh. 1.7 - Prob. 64ECh. 1.7 - Prob. 65ECh. 1.7 - Prob. 66ECh. 1.7 - Prob. 67ECh. 1.7 - Prob. 68ECh. 1.7 - Prob. 69ECh. 1.7 - Prob. 70ECh. 1.7 - Prob. 71ECh. 1.7 - Prob. 72ECh. 1.8 - Prob. 1ECh. 1.8 - Prob. 2ECh. 1.8 - Prob. 3ECh. 1.8 - Prob. 4ECh. 1.8 - Prob. 5ECh. 1.8 - Prob. 6ECh. 1.8 - Prob. 7ECh. 1.8 - Prob. 8ECh. 1.8 - Prob. 9ECh. 1.8 - Prob. 10ECh. 1.8 - Prob. 11ECh. 1.8 - Prob. 12ECh. 1.8 - Prob. 13ECh. 1.8 - Prob. 14ECh. 1.8 - Prob. 15ECh. 1.8 - Prob. 16ECh. 1.8 - Prob. 17ECh. 1.8 - Prob. 18ECh. 1.8 - Prob. 19ECh. 1.8 - Prob. 20ECh. 1.8 - Prob. 21ECh. 1.8 - Prob. 22ECh. 1.8 - Prob. 23ECh. 1.8 - Prob. 24ECh. 1.8 - Prob. 25ECh. 1.8 - Prob. 26ECh. 1.8 - Prob. 27ECh. 1.8 - Prob. 28ECh. 1.8 - Prob. 29ECh. 1.8 - Prob. 30ECh. 1.8 - Prob. 31ECh. 1.8 - Prob. 32ECh. 1.8 - Prob. 33ECh. 1.8 - Prob. 34ECh. 1.8 - Prob. 35ECh. 1.8 - Prob. 36ECh. 1.8 - Prob. 37ECh. 1.8 - Prob. 38ECh. 1.8 - Prob. 39ECh. 1.8 - Prob. 40ECh. 1.8 - Prob. 41ECh. 1.8 - Prob. 42ECh. 1.8 - Prob. 43ECh. 1.8 - Prob. 44ECh. 1.8 - Prob. 45ECh. 1.8 - Prob. 46ECh. 1.8 - Prob. 47ECh. 1.8 - Prob. 48ECh. 1.8 - Prob. 49ECh. 1.8 - Prob. 50ECh. 1.8 - Prob. 51ECh. 1.8 - Prob. 52ECh. 1.8 - Prob. 53ECh. 1.8 - Prob. 54ECh. 1.8 - Prob. 55ECh. 1.8 - Prob. 56ECh. 1.8 - Prob. 57ECh. 1.8 - Prob. 58ECh. 1.8 - Prob. 59ECh. 1.8 - Prob. 60ECh. 1.8 - Prob. 61ECh. 1.8 - Prob. 62ECh. 1.8 - Prob. 63ECh. 1.8 - Prob. 64ECh. 1.8 - Prob. 65ECh. 1.8 - Prob. 66ECh. 1.8 - Prob. 67ECh. 1.8 - Prob. 68ECh. 1.8 - Prob. 69ECh. 1.8 - Prob. 70ECh. 1.8 - Prob. 71ECh. 1.8 - Prob. 72ECh. 1.8 - Prob. 73ECh. 1.9 - Prob. 1ECh. 1.9 - Prob. 2ECh. 1.9 - Prob. 3ECh. 1.9 - Prob. 4ECh. 1.9 - Prob. 5ECh. 1.9 - Prob. 6ECh. 1.9 - Prob. 7ECh. 1.9 - Prob. 8ECh. 1.9 - Prob. 9ECh. 1.9 - Prob. 10ECh. 1.9 - Prob. 11ECh. 1.9 - Prob. 12ECh. 1.9 - Prob. 13ECh. 1.9 - Prob. 14ECh. 1.9 - Prob. 15ECh. 1.9 - Prob. 16ECh. 1.9 - Prob. 17ECh. 1.9 - Prob. 18ECh. 1.9 - Prob. 19ECh. 1.9 - Prob. 20ECh. 1.9 - Prob. 21ECh. 1.9 - Prob. 22ECh. 1.9 - Prob. 23ECh. 1.9 - Prob. 24ECh. 1.9 - Prob. 25ECh. 1.9 - Prob. 26ECh. 1.9 - Prob. 27ECh. 1.9 - Prob. 28ECh. 1.9 - Prob. 29ECh. 1.9 - Prob. 30ECh. 1.9 - Prob. 31ECh. 1.9 - Prob. 32ECh. 1.9 - Prob. 33ECh. 1.9 - Prob. 34ECh. 1.9 - Prob. 35ECh. 1.9 - Prob. 36ECh. 1.9 - Prob. 37ECh. 1.9 - Prob. 38ECh. 1.9 - Prob. 39ECh. 1.9 - Prob. 40ECh. 1.9 - Prob. 41ECh. 1.9 - Prob. 42ECh. 1.9 - Prob. 43ECh. 1.9 - Prob. 44ECh. 1.9 - Prob. 45ECh. 1.9 - Prob. 46ECh. 1.9 - Prob. 47ECh. 1.9 - Prob. 48ECh. 1.9 - Prob. 49ECh. 1.9 - Prob. 50ECh. 1.9 - Prob. 51ECh. 1.9 - Prob. 52ECh. 1.9 - Prob. 53ECh. 1.9 - Prob. 54ECh. 1.9 - Prob. 55ECh. 1.9 - Prob. 56ECh. 1.9 - Prob. 57ECh. 1.9 - Prob. 58ECh. 1.9 - Prob. 59ECh. 1.9 - Prob. 60ECh. 1.9 - Prob. 61ECh. 1.9 - Prob. 62ECh. 1.9 - Prob. 63ECh. 1.9 - Prob. 64ECh. 1.9 - Prob. 65ECh. 1.9 - Prob. 66ECh. 1.9 - Prob. 67ECh. 1.9 - Prob. 68ECh. 1.9 - Prob. 69ECh. 1.9 - Prob. 70ECh. 1.9 - Prob. 71ECh. 1.9 - Prob. 72ECh. 1.9 - Prob. 73ECh. 1.9 - Prob. 74ECh. 1.9 - Prob. 75ECh. 1.9 - Prob. 76ECh. 1.9 - Prob. 77ECh. 1.9 - Prob. 78ECh. 1.9 - Prob. 79ECh. 1.9 - Prob. 80ECh. 1.9 - Prob. 81ECh. 1.9 - Prob. 82ECh. 1.9 - Prob. 83ECh. 1.9 - Prob. 84ECh. 1.9 - Prob. 85ECh. 1.9 - Prob. 86ECh. 1.9 - Prob. 87ECh. 1.9 - Prob. 88ECh. 1.9 - Prob. 89ECh. 1.9 - Prob. 90ECh. 1.9 - Prob. 91ECh. 1.9 - Prob. 92ECh. 1.9 - Prob. 93ECh. 1.9 - Prob. 94ECh. 1.9 - Prob. 95ECh. 1.9 - Prob. 96ECh. 1.9 - Prob. 97ECh. 1.9 - Prob. 98ECh. 1.9 - Prob. 99ECh. 1.9 - Prob. 100ECh. 1.9 - Prob. 101ECh. 1.9 - Prob. 102ECh. 1.10 - Prob. 1ECh. 1.10 - Prob. 2ECh. 1.10 - Prob. 3ECh. 1.10 - Prob. 4ECh. 1.10 - Prob. 5ECh. 1.10 - Prob. 6ECh. 1.10 - Prob. 7ECh. 1.10 - Prob. 8ECh. 1.10 - Prob. 9ECh. 1.10 - Prob. 10ECh. 1.10 - Prob. 11ECh. 1.10 - Prob. 12ECh. 1.10 - Prob. 13ECh. 1.10 - Prob. 14ECh. 1.10 - Prob. 15ECh. 1.10 - Prob. 16ECh. 1.10 - Prob. 17ECh. 1.10 - Prob. 18ECh. 1.10 - Prob. 19ECh. 1.10 - Prob. 20ECh. 1.10 - Prob. 21ECh. 1.10 - Prob. 22ECh. 1.10 - Prob. 23ECh. 1.10 - Prob. 24ECh. 1.10 - Prob. 25ECh. 1.10 - Prob. 26ECh. 1.10 - Prob. 27ECh. 1.10 - Prob. 28ECh. 1.10 - Prob. 29ECh. 1.10 - Prob. 30ECh. 1.10 - Prob. 31ECh. 1.10 - Prob. 32ECh. 1.10 - Prob. 33ECh. 1.10 - Prob. 34ECh. 1.10 - Prob. 35ECh. 1.10 - Prob. 36ECh. 1.10 - Prob. 37ECh. 1.10 - Prob. 38ECh. 1.10 - Prob. 39ECh. 1.10 - Prob. 40ECh. 1.10 - Prob. 41ECh. 1.10 - Prob. 42ECh. 1.10 - Prob. 43ECh. 1.10 - Prob. 44ECh. 1.10 - Prob. 45ECh. 1.10 - Prob. 46ECh. 1.10 - Prob. 47ECh. 1.10 - Prob. 48ECh. 1.10 - Prob. 49ECh. 1.10 - Prob. 50ECh. 1.10 - Prob. 51ECh. 1.10 - Prob. 52ECh. 1.10 - Prob. 53ECh. 1.10 - Prob. 54ECh. 1.10 - Prob. 55ECh. 1.10 - Prob. 56ECh. 1.10 - Prob. 57ECh. 1.10 - Prob. 58ECh. 1.10 - Prob. 59ECh. 1.10 - Prob. 60ECh. 1.10 - Prob. 61ECh. 1.10 - Prob. 62ECh. 1.10 - Prob. 63ECh. 1.10 - Prob. 64ECh. 1.10 - Prob. 65ECh. 1.10 - Prob. 66ECh. 1.10 - Prob. 67ECh. 1.10 - Prob. 68ECh. 1.10 - Prob. 69ECh. 1.10 - Prob. 70ECh. 1.10 - Prob. 71ECh. 1.10 - Prob. 72ECh. 1.10 - Prob. 73ECh. 1.10 - Prob. 74ECh. 1.10 - Prob. 75ECh. 1.10 - Prob. 76ECh. 1.10 - Prob. 77ECh. 1.10 - Prob. 78ECh. 1.10 - Prob. 79ECh. 1 - Prob. 1RECh. 1 - Prob. 2RECh. 1 - Prob. 3RECh. 1 - Prob. 4RECh. 1 - Prob. 5RECh. 1 - Prob. 6RECh. 1 - Prob. 7RECh. 1 - Prob. 8RECh. 1 - Prob. 9RECh. 1 - Prob. 10RECh. 1 - Prob. 11RECh. 1 - Prob. 12RECh. 1 - Prob. 13RECh. 1 - Prob. 14RECh. 1 - Prob. 15RECh. 1 - Prob. 16RECh. 1 - Prob. 17RECh. 1 - Prob. 18RECh. 1 - Prob. 19RECh. 1 - Prob. 20RECh. 1 - Prob. 21RECh. 1 - Prob. 22RECh. 1 - Prob. 23RECh. 1 - Prob. 24RECh. 1 - Prob. 25RECh. 1 - Prob. 26RECh. 1 - Prob. 27RECh. 1 - Prob. 28RECh. 1 - Prob. 29RECh. 1 - Prob. 30RECh. 1 - Prob. 31RECh. 1 - Prob. 32RECh. 1 - Prob. 33RECh. 1 - Prob. 34RECh. 1 - Prob. 35RECh. 1 - Prob. 36RECh. 1 - Prob. 37RECh. 1 - Prob. 38RECh. 1 - Prob. 39RECh. 1 - Prob. 40RECh. 1 - Prob. 41RECh. 1 - Prob. 42RECh. 1 - Prob. 43RECh. 1 - Prob. 44RECh. 1 - Prob. 45RECh. 1 - Prob. 46RECh. 1 - Prob. 47RECh. 1 - Prob. 48RECh. 1 - Prob. 49RECh. 1 - Prob. 50RECh. 1 - Prob. 51RECh. 1 - Prob. 52RECh. 1 - Prob. 53RECh. 1 - Prob. 54RECh. 1 - Prob. 55RECh. 1 - Prob. 56RECh. 1 - Prob. 57RECh. 1 - Prob. 58RECh. 1 - Prob. 59RECh. 1 - Prob. 60RECh. 1 - Prob. 61RECh. 1 - Prob. 62RECh. 1 - Prob. 63RECh. 1 - Prob. 64RECh. 1 - Prob. 65RECh. 1 - Prob. 66RECh. 1 - Prob. 67RECh. 1 - Prob. 68RECh. 1 - Prob. 69RECh. 1 - Prob. 70RECh. 1 - Prob. 71RECh. 1 - Prob. 72RECh. 1 - Prob. 73RECh. 1 - Prob. 74RECh. 1 - Prob. 75RECh. 1 - Prob. 76RECh. 1 - Prob. 77RECh. 1 - Prob. 78RECh. 1 - Prob. 79RECh. 1 - Prob. 80RECh. 1 - Prob. 81RECh. 1 - Prob. 82RECh. 1 - Prob. 83RECh. 1 - Prob. 84RECh. 1 - Prob. 85RECh. 1 - Prob. 86RECh. 1 - Prob. 87RECh. 1 - Prob. 88RECh. 1 - Prob. 89RECh. 1 - Prob. 90RECh. 1 - Prob. 91RECh. 1 - Prob. 92RECh. 1 - Prob. 93RECh. 1 - Prob. 94RECh. 1 - Prob. 95RECh. 1 - Prob. 96RECh. 1 - Prob. 97RECh. 1 - Prob. 98RECh. 1 - Prob. 99RECh. 1 - Prob. 1CTCh. 1 - Prob. 2CTCh. 1 - Prob. 3CTCh. 1 - Prob. 4CTCh. 1 - Prob. 5CTCh. 1 - Prob. 6CTCh. 1 - Prob. 7CTCh. 1 - Prob. 8CTCh. 1 - Prob. 9CTCh. 1 - Prob. 10CTCh. 1 - Prob. 11CTCh. 1 - Prob. 12CTCh. 1 - Prob. 13CTCh. 1 - Prob. 14CTCh. 1 - Prob. 15CTCh. 1 - Prob. 16CTCh. 1 - Prob. 17CTCh. 1 - Prob. 18CTCh. 1 - Prob. 19CTCh. 1 - Prob. 20CTCh. 1 - Prob. 21CTCh. 1 - Prob. 22CTCh. 1 - Prob. 23CTCh. 1 - Prob. 24CTCh. 1 - Prob. 25CTCh. 1 - Prob. 26CTCh. 1 - Prob. 1PSCh. 1 - Prob. 2PSCh. 1 - Prob. 3PSCh. 1 - Prob. 4PSCh. 1 - Prob. 5PSCh. 1 - Prob. 6PSCh. 1 - Prob. 7PSCh. 1 - Prob. 8PSCh. 1 - Prob. 9PSCh. 1 - Prob. 10PSCh. 1 - Prob. 11PSCh. 1 - Prob. 12PSCh. 1 - Prob. 13PSCh. 1 - Prob. 14PSCh. 1 - Prob. 15PS
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, calculus and related others by exploring similar questions and additional content below.Similar questions
- 3. P 2. 1 -3-2-10 1 2 3 -2- X The graph of point P is given in the xy-plane. Which of the following are possible polar coordinates of point P? A Ⓐ(2, 2) (2, 1/1/1) B (2, 3) C Ⓒ =) (2√2, 41 ) D (2√2, 3) 4arrow_forwardThe graph of f' is below. Use it to determine where the local minima and maxima for f are. If there are multiple answers, separate with commas. 2 f'(x) N -5 -4 3-2-1 -1 -2 -3 -4 12 3 4 5 -x Local minima at x Local maxima at xarrow_forwardThe graph of f' is below. Use it to determine the intervals where f is increasing. -5-4-32 4- 3 2 1 -2 -3 +x 2 3 4 5arrow_forward
- The graph of f' is below. Use it to determine where the inflection points are and the intervals where f is concave up and concave down. If there are multiple inflection points, separate with a comma. 6 5 4 3 2 1 f'(x) +x -6-5-4-3 -2 -1 1 2 3 4 5 6 -1 -2 -3 -4 -5 -6+ Inflection point(s) at x = Concave up: Concave down:arrow_forwardThe graph of f' is below. Use it to determine where the local minima and maxima for f are. If there are multiple answers, separate with commas. f'(x) 4- -5-4-3-8-1 3 2 1 x 1 2 3 4 5 -1 -2 -3 -4 Local minima at a Local maxima at =arrow_forwardThe graph of f' is below. Use it to determine the intervals where f is increasing. f'(xx) 4- -5 -3 -2 3 2 1 1 2 3 4 5 Cit +x 7 2arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning
Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON
Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning
Calculus: Early Transcendentals
Calculus
ISBN:9781285741550
Author:James Stewart
Publisher:Cengage Learning
Thomas' Calculus (14th Edition)
Calculus
ISBN:9780134438986
Author:Joel R. Hass, Christopher E. Heil, Maurice D. Weir
Publisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)
Calculus
ISBN:9780134763644
Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric Schulz
Publisher:PEARSON
Calculus: Early Transcendentals
Calculus
ISBN:9781319050740
Author:Jon Rogawski, Colin Adams, Robert Franzosa
Publisher:W. H. Freeman
Calculus: Early Transcendental Functions
Calculus
ISBN:9781337552516
Author:Ron Larson, Bruce H. Edwards
Publisher:Cengage Learning
Algebraic Complexity with Less Relations; Author: The University of Chicago;https://www.youtube.com/watch?v=ZOKM1JPz650;License: Standard Youtube License
Strassen's Matrix Multiplication - Divide and Conquer - Analysis of Algorithm; Author: Ekeeda;https://www.youtube.com/watch?v=UnpySHwAJsQ;License: Standard YouTube License, CC-BY
Trigonometric Equations with Complex Numbers | Complex Analysis #6; Author: TheMathCoach;https://www.youtube.com/watch?v=zdD8Dab1T2Y;License: Standard YouTube License, CC-BY