
Concept explainers
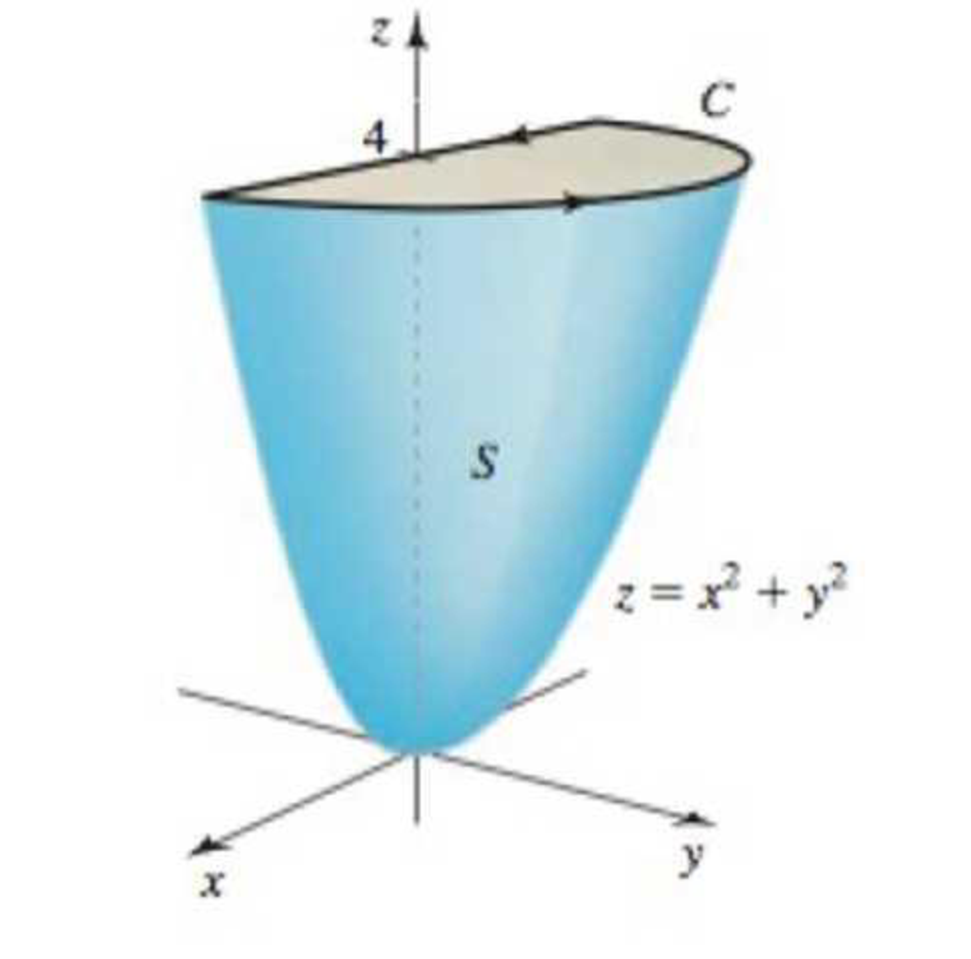
Compound surface and boundary Begin with the paraboloid z = x2 + y2, for 0 ≤ z ≤ 4, and slice it with the plane y = 0. Let S be the surface that remains for y ≥ 0 (including the planar surface in the xz–plane) (see figure). Let C be the semicircle and line segment that bound the cap of .S in the plane z = 4 with counterclockwise orientation. Let F = 〈2z + y, 2x + z, 2y + x〉.
a. Describe the direction of the
b. Evaluate
c. Evaluate
Want to see the full answer?
Check out a sample textbook solution
Chapter 14 Solutions
CODE/CALC ET 3-HOLE
Additional Engineering Textbook Solutions
Calculus: Early Transcendentals (2nd Edition)
Basic Business Statistics, Student Value Edition
Elementary Statistics: Picturing the World (7th Edition)
Algebra and Trigonometry (6th Edition)
College Algebra with Modeling & Visualization (5th Edition)
Elementary Statistics
- Show that the Laplace equation in Cartesian coordinates: J²u J²u + = 0 მx2 Jy2 can be reduced to the following form in cylindrical polar coordinates: 湯( ди 1 8²u + Or 7,2 მ)2 = 0.arrow_forwardFind integrating factorarrow_forwardDraw the vertical and horizontal asymptotes. Then plot the intercepts (if any), and plot at least one point on each side of each vertical asymptote.arrow_forward
- Draw the asymptotes (if there are any). Then plot two points on each piece of the graph.arrow_forwardCancel Done RESET Suppose that R(x) is a polynomial of degree 7 whose coefficients are real numbers. Also, suppose that R(x) has the following zeros. -1-4i, -3i, 5+i Answer the following. (a) Find another zero of R(x). ☐ | | | | |│ | | | -1 བ ¢ Live Adjust Filters Croparrow_forwardSuppose that R (x) is a polynomial of degree 7 whose coefficients are real numbers. Also, suppose that R (x) has the following zeros. -1-4i, -3i, 5+i Answer the following. (c) What is the maximum number of nonreal zeros that R (x) can have? ☐arrow_forward
- Suppose that R (x) is a polynomial of degree 7 whose coefficients are real numbers. Also, suppose that R (x) has the following zeros. -1-4i, -3i, 5+i Answer the following. (b) What is the maximum number of real zeros that R (x) can have? ☐arrow_forwardi need help please dont use chat gptarrow_forward3.1 Limits 1. If lim f(x)=-6 and lim f(x)=5, then lim f(x). Explain your choice. x+3° x+3* x+3 (a) Is 5 (c) Does not exist (b) is 6 (d) is infinitearrow_forward
- 1 pts Let F and G be vector fields such that ▼ × F(0, 0, 0) = (0.76, -9.78, 3.29), G(0, 0, 0) = (−3.99, 6.15, 2.94), and G is irrotational. Then sin(5V (F × G)) at (0, 0, 0) is Question 1 -0.246 0.072 -0.934 0.478 -0.914 -0.855 0.710 0.262 .arrow_forward2. Answer the following questions. (A) [50%] Given the vector field F(x, y, z) = (x²y, e", yz²), verify the differential identity Vx (VF) V(V •F) - V²F (B) [50%] Remark. You are confined to use the differential identities. Let u and v be scalar fields, and F be a vector field given by F = (Vu) x (Vv) (i) Show that F is solenoidal (or incompressible). (ii) Show that G = (uvv – vVu) is a vector potential for F.arrow_forwardA driver is traveling along a straight road when a buffalo runs into the street. This driver has a reaction time of 0.75 seconds. When the driver sees the buffalo he is traveling at 44 ft/s, his car can decelerate at 2 ft/s^2 when the brakes are applied. What is the stopping distance between when the driver first saw the buffalo, to when the car stops.arrow_forward
 Elementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage,Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage
Elementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage,Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage Linear Algebra: A Modern IntroductionAlgebraISBN:9781285463247Author:David PoolePublisher:Cengage Learning
Linear Algebra: A Modern IntroductionAlgebraISBN:9781285463247Author:David PoolePublisher:Cengage Learning Trigonometry (MindTap Course List)TrigonometryISBN:9781337278461Author:Ron LarsonPublisher:Cengage Learning
Trigonometry (MindTap Course List)TrigonometryISBN:9781337278461Author:Ron LarsonPublisher:Cengage Learning



