
Concept explainers
Equipotential curves Consider the following potential functions and graphs of their equipotential curves.
a. Find the associated gradient field F = ▿ϕ.
b. Show that the
c. Show that the vector field is orthogonal to the equipotential curve at all points (x, y).
d. Sketch two flow curves representing F that are everywhere orthogonal to the equipotential curves.
37. ϕ (x, y) = 2x +3y
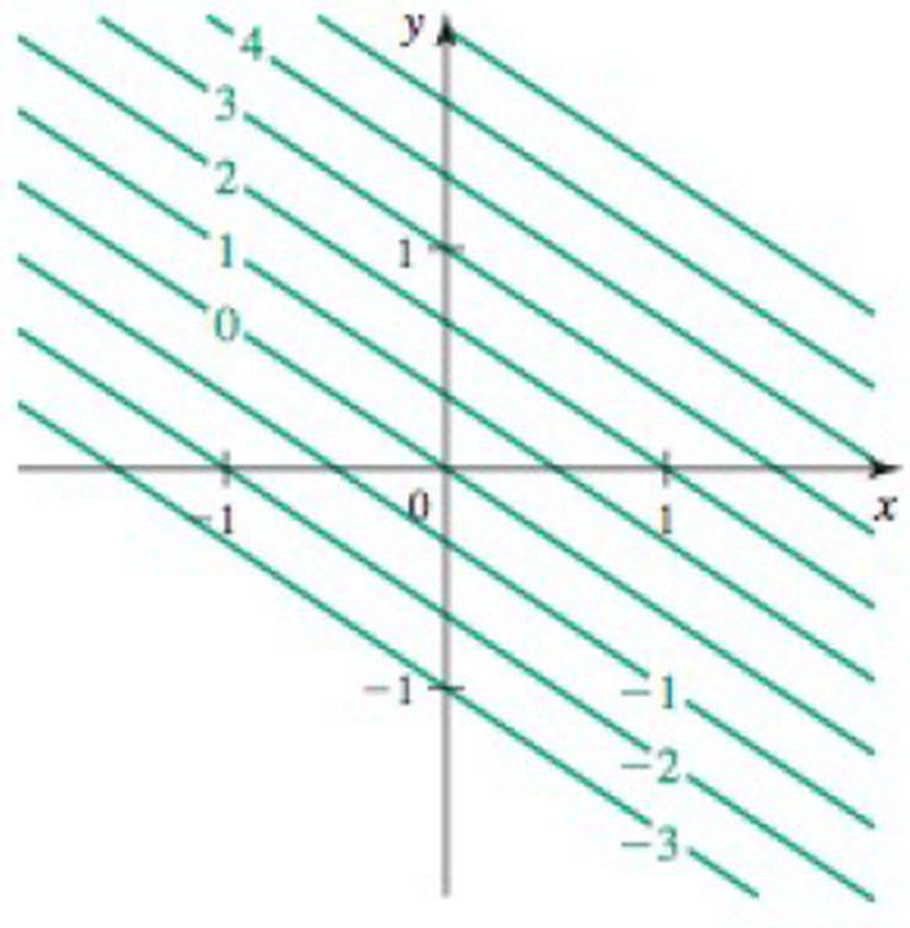
Trending nowThis is a popular solution!

Chapter 14 Solutions
Calculus: Early Transcendentals (2nd Edition)
Additional Math Textbook Solutions
Calculus: Early Transcendentals (2nd Edition)
Elementary Statistics
Thinking Mathematically (6th Edition)
Elementary Statistics: Picturing the World (7th Edition)
University Calculus: Early Transcendentals (4th Edition)
Pre-Algebra Student Edition
- 4 Consider f(x) periodic function with period 2, coinciding with (x) = -x on the interval [,0) and being the null function on the interval [0,7). The Fourier series of f: (A) does not converge in quadratic norm to f(x) on [−π,π] (B) is pointwise convergent to f(x) for every x = R П (C) is in the form - 4 ∞ +Σ ak cos(kx) + bk sin(kx), ak ‡0, bk ‡0 k=1 (D) is in the form ak cos(kx) + bk sin(kx), ak 0, bk 0 k=1arrow_forwardSolve the equation.arrow_forwardcould you explain this pleasearrow_forward
- the answer is C, could you show me how to do itarrow_forward7. [-/1 Points] DETAILS MY NOTES SESSCALCET2 6.1.505.XP. Evaluate the integral. (Use C for the constant of integration.) 21z³e² dz | 21 Need Help? Read It SUBMIT ANSWER 8. [-/1 Points] DETAILS MY NOTES SESSCALCET2 6.1.020. Evaluate the integral. 36 In y dy ₤36 25 Need Help? Read It SUBMIT ANSWER 9. [-/1 Points] DETAILS MY NOTES SESSCALCET2 6.1.009. Evaluate the integral. (Use C for the constant of integration.) In(7x In(7x + 1) dxarrow_forward10. [-/1 Points] DETAILS MY NOTES SESSCALCET2 6.1.506.XP. Evaluate the integral. √xy dy Need Help? Read It Watch It SUBMIT ANSWER 11. [-/1 Points] DETAILS MY NOTES SESSCALCET2 6.1.023. Evaluate the integral. 1/2 7 cos-1 x dx Need Help? Read It Watch It SUBMIT ANSWER 12. [-/1 Points] DETAILS MY NOTES SESSCALCET2 6.1.507.XP. Evaluate the integral. L² 0 (In x)² x3 dx Need Help? Read Itarrow_forward
- i attached the question and the way i solved it, i believe i made an error, could you point it out for me because the correct answer is 3pi/2correct answer is D, please see both attached photosarrow_forwardQuestion 3 and 4arrow_forwardcould you explain this using stoke theoremi already circled the correct answerarrow_forward
- Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage
 Algebra and Trigonometry (MindTap Course List)AlgebraISBN:9781305071742Author:James Stewart, Lothar Redlin, Saleem WatsonPublisher:Cengage Learning
Algebra and Trigonometry (MindTap Course List)AlgebraISBN:9781305071742Author:James Stewart, Lothar Redlin, Saleem WatsonPublisher:Cengage Learning

