Chapter 10, Problem 40P

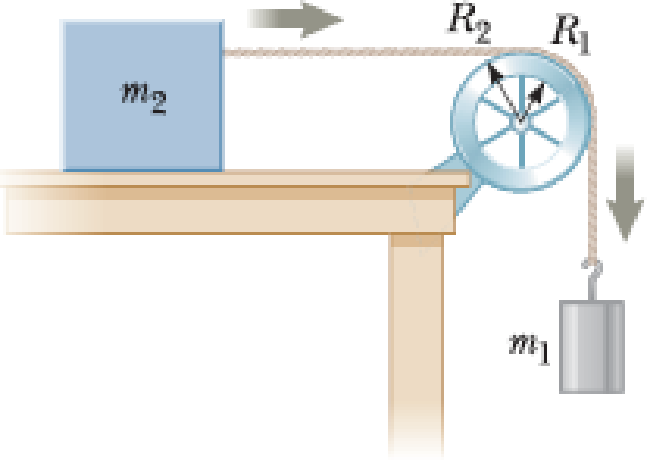
In Figure P10.40, the hanging object has a mass of m₁ = 0.420 kg; the sliding block has a mass of m₂ = 0.850 kg; and the pulley is a hollow cylinder with a mass of M = 0.350 kg, an inner radius of R₁ = 0.020 0 m, and an outer radius of R₂ = 0.030 0 m. Assume the mass of the spokes is negligible. The coefficient of kinetic friction between the block and the horizontal surface is μ_k = 0.250. The pulley turns without friction on its axle. The light cord does not stretch and does not slip on the pulley. The block has a velocity of v_i = 0.820 m/s toward the pulley when it passes a reference point on the table. (a) Use energy methods to predict its speed after it has moved to a second point, 0.700 m away. (b) Find the angular speed of the pulley at the same moment.

Figure P10.40

To determine

The speed of the lock after moved to a second point.

Answer to Problem 40P

The speed of the lock after moved to a second point is $\underset{\_}{1.59\text{m}/\text{s}}$.

Explanation of Solution

According to law of conservation of energy the total energy of the system is remains constant.

Write the expression for the conservation of energy of the system.

  $\begin{array}{c}\Delta K+\Delta U+\Delta E_{\text{int}}=0\\ \left(K_f-K_i\right)+\left(U_f-U_i\right)+\Delta E_{\text{int}}=0\end{array}$        (I)

Here, $K_f$ is the final kinetic energy, $K_i$ is the final kinetic energy, $U_f$ is the final potential energy, $U_i$ is the initial potential energy, $\Delta E_{\text{int}}$ is the energy lost due to friction.

The initial kinetic energy involves the kinetic energy of the hanging block, the sliding block, rotational kinetic energy, and the final kinetic energy involves the final kinetic energy of hanging block, the sliding block, rotational kinetic energy.

Write the expression for the initial kinetic energy.

  $K_i=\frac{1}{2}{m}_1{\upsilon }_i^2+\frac{1}{2}{m}_2{\upsilon }_i^2$        (II)

Here, $m_1$ is the mass of the hanging block, $m_2$ is the mass of the sliding block, ${\upsilon }_i$ is the initial velocity.

Write the expression for the final kinetic energy.

  $K_f=\frac{1}{2}{m}_1{\upsilon }^2+\frac{1}{2}{m}_2{\upsilon }^2$        (III)

Here, $\upsilon$ is the final velocity.

Write the expression for the change in rotational kinetic energy.

  $\Delta K_{\text{rot}}=\frac{1}{2}I{\omega }^2-\frac{1}{2}I{\omega }_i^2$        (IV)

Here, $I$ is the moment of inertia, ${\omega }_i$ is the initial angular velocity, $\omega$ is the final angular velocity.

Write the expression energy lost due to friction.

  $\Delta E_{\text{int}}=f_{k}d$        (V)

Here, $f_k$ is the force due to kinetic friction, $d$ is the distance moved by the mass $m_2$.

Substitute, $\mu m_{2}g$ for $f_k$ in equation (V).

  $\Delta E_{\text{int}}=\mu m_{2}gd$        (VI)

Here, $\mu$ is the coefficient of kinetic friction, $g$ is the acceleration due to gravity.

Write expression for change in potential energy.

  $U_f-U_i=m_{1}gy-m_{1}g{y}_i$        (VII)

Substitute, equation (VII), (VI), (IV), (III), (II) in equation (I).

  $\begin{array}{c}\left(\left(\frac{1}{2}{m}_1{\upsilon }^2+\frac{1}{2}{m}_2{\upsilon }^2\right)-\left(\frac{1}{2}{m}_1{\upsilon }_i^2+\frac{1}{2}{m}_2{\upsilon }_i^2\right)\right)+\left(\frac{1}{2}I{\omega }^2-\frac{1}{2}I{\omega }_i^2\right)+\left(m_{1}gy-m_{1}g{y}_i\right)+\mu m_{2}gd=0\\ \frac{1}{2}\left(m_1+m_2\right)\left({\upsilon }^2-{\upsilon }_i^2\right)+\frac{1}{2}I\left({\omega }^2-{\omega }_i^2\right)+m_{1}g\left(y-y_1\right)+\mu m_{2}gd=0\end{array}$        (VIII)

Substitute, $\frac{1}{2}M\left(R_1^2+R_1^2\right)$ for $I$, $\frac{\upsilon }{R}$ for $\omega$, $\frac{{\upsilon }_i}{R}$ for ${\omega }_i$ in equation (VIII).

$\begin{array}{c}\frac{1}{2}\left(m_1+m_2\right)\left({\upsilon }^2-{\upsilon }_i^2\right)+\frac{1}{2}\left[\frac{1}{2}M\left(R_1^2+R_2^2\right)\right]\left({\left(\frac{\upsilon }{R}\right)}^2-{\left(\frac{{\upsilon }_i}{R}\right)}^2\right)+m_{1}g\left(-d\right)+\mu m_{2}gd=0\\ \frac{1}{2}\left(m_1+m_2\right)\left({\upsilon }^2-{\upsilon }_i^2\right)+\frac{1}{2}\left[\frac{1}{2}M\left(\frac{R_1^2}{R_2^2}+1\right)\right]\left({\upsilon }^2-{\upsilon }_i{}^2\right)=gd\left(m_1-\mu m_2\right)\\ \frac{1}{2}\left[\left(m_1+m_2\right)+\frac{1}{2}M\left(\frac{R_1^2}{R_2^2}+1\right)\right]\left({\upsilon }^2-{\upsilon }_i{}^2\right)=gd\left(m_1-\mu m_2\right)\\ \upsilon ={\left\{{\upsilon }_i{}^2+\frac{4gd\left(m_1-\mu m_2\right)}{2\left(m_1+m_2\right)+\frac{1}{2}M\left(\frac{R_1^2}{R_2^2}+1\right)}\right\}}^{1/2}\end{array}$        (IX)

Here, $M$ is the mass of the hollow cylinder, $R_1$ is the inner radius of the cylinder, $R_2$ is the outer radius of the cylinder.

Conclusion:

Substitute, $0.820\text{m}/\text{s}$ for ${\upsilon }_i$, $9.80\text{m}/{\text{s}}^{\text{2}}$ for $g$, $0.420\text{kg}$ for $m_1$, $0.250$ for $\mu$, $0.850\text{kg}$ for $m_2$, $0.350\text{kg}$, $0.020\text{m}$ for $R_1$, and $0.030\text{m}$ for $R_2$, $0.700\text{m}$ for $d$ in equation (IX).

$\begin{array}{c}\upsilon ={\left\{{\left(0.820\text{m}/\text{s}\right)}^2+\frac{4\left(9.80\text{m}/{\text{s}}^{\text{2}}\right)\left(0.700\text{m}\right)\left(0.420\text{kg}-\left(0.250\right)\left(0.850\text{kg}\right)\right)}{2\left(0.420\text{kg}+0.850\text{kg}\right)+\frac{1}{2}\left(0.350\text{kg}\right)\left(\frac{{\left(0.020\text{m}\right)}^2}{\left(0.030\text{m}\right)}+1\right)}\right\}}^{1/2}\\ =1.59\text{m}/\text{s}\end{array}$

Therefore, speed of the lock after moved to a second point is $\underset{\_}{1.59\text{m}/\text{s}}$.

To determine

The angular speed of the pulley.

Answer to Problem 40P

The angular speed of the pulley is $\underset{\_}{53.1\text{rad}/\text{s}}$.

Explanation of Solution

Write the expression for angular speed of the pulley.

  $\omega =\frac{\upsilon }{r}$        (X)

Conclusion:

Substitute, $1.59\text{m}/\text{s}$ for $\upsilon$, $0.030\text{m}$ for $r$ in equation (X) to find $\omega$.

  $\begin{array}{c}\omega =\frac{1.59\text{m}/\text{s}}{0.030\text{m}}\\ =53.1\text{rad}/\text{s}\end{array}$

Therefore, the angular speed of the pulley is $\underset{\_}{53.1\text{rad}/\text{s}}$.