
Concept explainers
Two astronauts (Fig. P10.67), each having a mass of 75.0 kg, are connected by a 10.0-m rope of negligible mass. They are isolated in space, orbiting their center of mass at speeds of 5.00 m/s. Treating the astronauts as particles, calculate
- (a) the magnitude of the
angular momentum of the two-astronaut system and - (b) the rotational energy of the system. By pulling on the rope, one astronaut shortens the distance between them to 5.00 m.
- (c) What is the new angular momentum of the system?
- (d) What are the astronauts’ new speeds?
- (e) What is the new rotational energy of the system?
- (f) How much chemical potential energy in the body of the astronaut was converted to mechanical energy in the system when he shortened the rope?
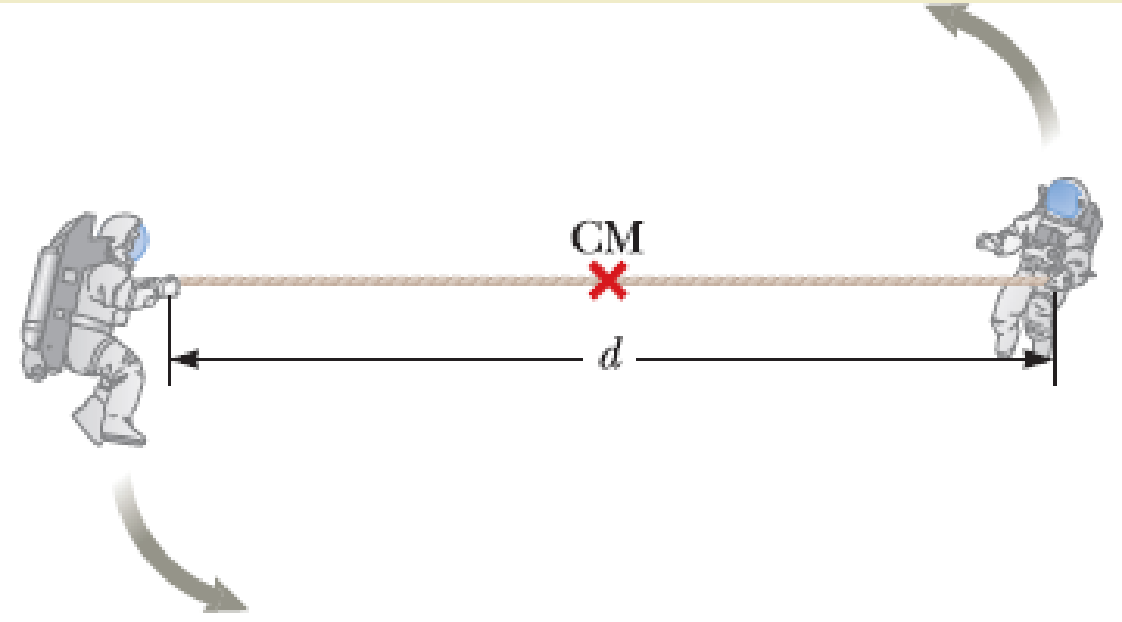
Figure P10.67 Problems 67 and 68.
(a)
The magnitude of angular momentum of the two astronaut system.
Answer to Problem 67P
The magnitude of angular momentum of the two astronaut system is
Explanation of Solution
Consider the figure given below.

Write the expression for the magnitude of angular momentum.
Here,
From figure
Conclusion:
Substitute,
Therefore, the magnitude of angular momentum of the two astronaut system is
(b)
The rotational kinetic energy of the system.
Answer to Problem 67P
The rotational kinetic energy of the system is
Explanation of Solution
The total rotational kinetic energy is the sum of the kinetic energy of two astronauts.
Write the expression for the rotational kinetic energy.
Here,
Conclusion:
The mass, and speed of two astronauts are same.
Substitute,
Therefore, the rotational kinetic energy of the system is
(c)
The angular momentum when one of the astronaut shortens the distance between them to
Answer to Problem 67P
The angular momentum when one of the astronaut shortens the distance between them to
Explanation of Solution
Even if the distance between the astronauts changed, the tension of the rope not generating ant torque about the center of mass. Since there is no change in torque the angular momentum of two astronaut –rope system will be same as that of the initial case
Since there is no outside torque the angular momentum when one of the astronaut shortens the distance between them to
Conclusion:
Therefore, the angular momentum when one of the astronaut shortens the distance between them to
(d)
The speed of the astronauts after shortening the distance.
Answer to Problem 67P
The speed of the astronauts after shortening the distance is
Explanation of Solution
Use equation (III) to find the new speed of the astronauts. The angular momentum of the system remains same even if he distance between the astronauts changes.
Conclusion:
Substitute,
Therefore, the speed of the astronauts after shortening the distance is
(f)
The new rotational kinetic energy of the system.
Answer to Problem 67P
The new rotational kinetic energy of the system is
Explanation of Solution
The total rotational kinetic energy is the sum of the kinetic energy of two astronauts.
Write the expression for the rotational kinetic energy.
Here,
Conclusion:
The mass, and speed of two astronauts are same.
Substitute,
Therefore, the rotational kinetic energy of the system is
(e)
The amount of chemical; energy converted to mechanical energy.
Answer to Problem 67P
The amount of chemical; energy converted to mechanical energy is
Explanation of Solution
The amount of chemical; energy converted to mechanical energy is equal to the work done by the astronaut. According to work energy theorem the work dine will be the change in rotational kinetic energy.
Write the expression for work done.
Conclusion:
Substitute,
Therefore, the amount of chemical; energy converted to mechanical energy is
Want to see more full solutions like this?
Chapter 10 Solutions
Principles of Physics: A Calculus-Based Text
- Solve and answer the problem correctly and be sure to check your work. Thank you!!arrow_forwardA 10-m-long glider with a mass of 680 kg (including the passengers) is gliding horizontally through the air at 28 m/s when a 60 kg skydiver drops out by releasing his grip on the glider. What is the glider's speed just after the skydiver lets go?arrow_forwardPROBLEM 2 A cube of mass m is placed in a rotating funnel. (The funnel is rotating around the vertical axis shown in the diagram.) There is no friction between the cube and the funnel but the funnel is rotating at just the right speed needed to keep the cube rotating with the funnel. The cube travels in a circular path of radius r, and the angle between the vertical and the wall of the funnel is 0. Express your answers to parts (b) and (c) in terms of m, r, g, and/or 0. (a) Sketch a free-body diagram for the cube. Show all the forces acting on it, and show the appropriate coordinate system to use for this problem. (b) What is the normal force acting on the cube? FN=mg58 (c) What is the speed v of the cube? (d) If the speed of the cube is different from what you determined in part (c), a force of friction is necessary to keep the cube from slipping in the funnel. If the funnel is rotating slower than it was above, draw a new free-body diagram for the cube to show which way friction…arrow_forward
- Circular turns of radius r in a race track are often banked at an angle θ to allow the cars to achieve higher speeds around the turns. Assume friction is not present. Write an expression for the tan(θ) of a car going around the banked turn in terms of the car's speed v, the radius of the turn r, and g so that the car will not move up or down the incline of the turn. tan(θ) =arrow_forwardThe character Min Min from Arms was a DLC character added to Super Smash Bros. Min Min’s arms are large springs, with a spring constant of 8.53 ⋅ 10^3 N/m, which she uses to punch and fling away her opponents. Min Min pushes her spring arm against Steve, who is not moving, compressing it 1.20 m as shown in figure A. Steve has a mass of 81.6 kg. Assuming she uses only the spring to launch Steve, how fast is Steve moving when the spring is no longer compressed? As Steve goes flying away he goes over the edge of the level, as shown in figure C. What is the magnitude of Steve’s velocity when he is 2.00 m below where he started?arrow_forwardSlinky dog whose middle section is a giant spring with a spring constant of 10.9 N/m. Woody, who has a mass of 0.412 kg, grabs onto the tail end of Slink and steps off the bed with no initial velocity and reaches the floor right as his velocity hits zero again. How high is the bed? What is Woody’s velocity halfway down? Enter just the magnitude of velocity.arrow_forward
- No chatgpt pls will upvotearrow_forwardA positive charge of 91 is located 5.11 m to the left of a negative charge 92. The charges have different magnitudes. On the line through the charges, the net electric field is zero at a spot 2.90 m to the right of the negative charge. On this line there are also two spots where the potential is zero. (a) How far to the left of the negative charge is one spot? (b) How far to the right of the negative charge is the other?arrow_forwardA charge of -3.99 μC is fixed in place. From a horizontal distance of 0.0423 m, a particle of mass 7.31 x 103 kg and charge -9.76 µC is fired with an initial speed of 84.1 m/s directly toward the fixed charge. How far does the particle travel before its speed is zero?arrow_forward
- a) What is the minimum tension in N that the cable must be able to support without breaking? Assume the cable is massless. T = b) If the cable can only support a tension of 10,000 N what is the highest mass the ball can have in kg? mm =arrow_forwardCurve Fitter CURVE FITTER Open Update Fit Save New Exclusion Rules Select Validation Data Polynomial Exponential Logarithmic Auto Fourier Fit Fit Duplicate Data Manual FILE DATA FIT TYPE FIT Harmonic Motion X us 0.45 mi ce 0.4 0.35 0.3 0.25 0.2 Residuals Plot Contour Plot Plot Prediction Bounds None VISUALIZATION Colormap Export PREFERENCES EXPORT Fit Options COA Fourier Equation Fit Plot x vs. t -Harmonic Motion a0+ a1*cos(x*w) + b1*sin(x*w) Number of terms Center and scale 1 ▸ Advanced Options Read about fit options Results Value Lower Upper 0.15 a0 0.1586 0.1551 0.1620 a1 0.0163 0.0115 0.0211 0.1 b1 0.0011 -0.0093 0.0115 W 1.0473 0.9880 1.1066 2 8 10 t 12 14 16 18 20 Goodness of Fit Value Table of Fits SSE 0.2671 Fit State Fit name Data Harmonic Motion x vs. t Fit type fourier1 R-square 0.13345 SSE DFE 0.26712 296 Adj R-sq 0.12467 RMSE 0.030041 # Coeff Valic R-square 0.1335 4 DFE 296.0000 Adj R-sq 0.1247 RMSE 0.0300arrow_forwardWhat point on the spring or different masses should be the place to measure the displacement of the spring? For instance, should you measure to the bottom of the hanging masses?arrow_forward
 Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning
Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning Glencoe Physics: Principles and Problems, Student...PhysicsISBN:9780078807213Author:Paul W. ZitzewitzPublisher:Glencoe/McGraw-Hill
Glencoe Physics: Principles and Problems, Student...PhysicsISBN:9780078807213Author:Paul W. ZitzewitzPublisher:Glencoe/McGraw-Hill Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning University Physics Volume 1PhysicsISBN:9781938168277Author:William Moebs, Samuel J. Ling, Jeff SannyPublisher:OpenStax - Rice University
University Physics Volume 1PhysicsISBN:9781938168277Author:William Moebs, Samuel J. Ling, Jeff SannyPublisher:OpenStax - Rice University





