Introduction To Finite Element Analysis And Design
2nd Edition
ISBN: 9781119078722
Author: Kim, Nam H., Sankar, Bhavani V., KUMAR, Ashok V., Author.
Publisher: John Wiley & Sons,
expand_more
expand_more
format_list_bulleted
Videos
Textbook Question
Chapter 1, Problem 37E
The uniaxial bar shown below can be modeled as a one-dimensional bar. The bar has the following properties:
a. Calculate the global matrix equation after applying boundary conditions.
b. Solve for the displacement
c. What is the element force P in the bar?
Expert Solution & Answer
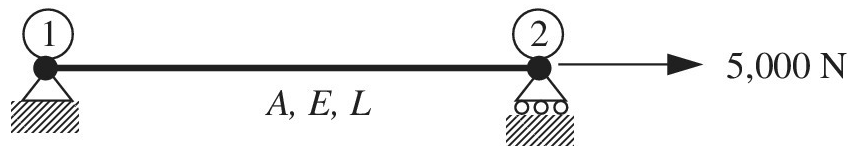
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
A solid bar of length L = 4 m and diameter 200 mm is heated from 20 to 320 degrees celsius and restrained between two solid immovable walls.
Young's modulus of the material is 90 GPa and the coefficient of thermal expansion is 22 x 10-6/°C.
→Calculate the thermal strain, e, in micro-strain correct to two decimal places.
micro-strain.
Calculate the thermal stress, o, in megapascals (MPa) correct to two decimal places.
E:
σ:
MPa.
Hence calculate the force exerted by the bar in meganewtons (MN) correct to two decimal places:
F
MN.
L
I need the answer quickly
A steel bar 300 mm long and having 24 mm diameter, is turned uuwn to 18 mm diameter for
one-third of its length. It is heated at 30°C above room temperature, clamped at both ends and
then allowed to cool to room temperature. If the distance between the clamps is unchanged,
the maximum stress in bar [a = 12.5 x 10/°C and E = 200 GN/m2] is
Q.3
Chapter 1 Solutions
Introduction To Finite Element Analysis And Design
Ch. 1 - Answer the following descriptive questions a....Ch. 1 - Calculate the displacement at node 2 and reaction...Ch. 1 - Repeat problem 2 by changing node numbers; that...Ch. 1 - Three rigid bodies, 2,3, and 4, are connected by...Ch. 1 - Three rigid bodies, 2,3, and 4, are connected by...Ch. 1 - Consider the spring-rigid body system described in...Ch. 1 - Four rigid bodies, 1, 2, 3, and 4, are connected...Ch. 1 - Determine the nodal displacements, element forces,...Ch. 1 - In the structure shown, rigid blocks are connected...Ch. 1 - The spring-mass system shown in the figure is in...
Ch. 1 - A structure is composed of two one-dimensional bar...Ch. 1 - Two rigid masses, 1 and 2, are connected by three...Ch. 1 - Use the finite element method to determine the...Ch. 1 - Consider a tapered bar of circular cross section....Ch. 1 - The stepped bar shown in the figure is subjected...Ch. 1 - Using the direct stiffness matrix method, find the...Ch. 1 - A stepped bar is clamped at one end and subjected...Ch. 1 - A stepped bar is clamped at both ends. A force of ...Ch. 1 - Repeat problem 18 for the stepped bar shown in the...Ch. 1 - The finite element equation for the uniaxial bar...Ch. 1 - The truss structure shown in the figure supports a...Ch. 1 - The properties of the two elements of a plane...Ch. 1 - For a two-dimensional truss structure as shown in...Ch. 1 - The 2D truss shown in the figure is assembled to...Ch. 1 - For a two-dimensional truss structure as shown in...Ch. 1 - The truss shown in the figure supports force Fat...Ch. 1 - Prob. 27ECh. 1 - In the finite element model of a plane truss in...Ch. 1 - Use the finite element method to solve the plane...Ch. 1 - The plane truss shown in the figure has two...Ch. 1 - Two bars are connected as shown in the figure....Ch. 1 - The truss structure shown in the figure supports...Ch. 1 - It is desired to use the finite element method to...Ch. 1 - Determine the member force and axial stress in...Ch. 1 - Determine the normal stress in each member of the...Ch. 1 - The space truss shown has four members. Determine...Ch. 1 - The uniaxial bar shown below can be modeled as a...Ch. 1 - In the structure shown below, the temperature of...Ch. 1 - Prob. 39ECh. 1 - The three-bar truss problem in figure 1.23 is...Ch. 1 - Use the finite element method to determine the...Ch. 1 - Repeat problem 41 for the new configuration with...Ch. 1 - Repeat problem 42 with an external force added to...Ch. 1 - The properties of the members of the truss in the...Ch. 1 - Repeat problem 44 for the truss on the right side...Ch. 1 - The truss shown in the figure supports the force ....Ch. 1 - The finite element method as used to solve the...Ch. 1 - Prob. 48E
Additional Engineering Textbook Solutions
Find more solutions based on key concepts
The volumetric flow rate and discharge velocity of the air.
Introduction to Heat Transfer
State if the members are in tension or compression. Prob. F6-10
INTERNATIONAL EDITION---Engineering Mechanics: Statics, 14th edition (SI unit)
What parts are included in the vehicle chassis?
Automotive Technology: Principles, Diagnosis, And Service (6th Edition) (halderman Automotive Series)
22. The Units Society Empire (USE) had defined the following set of "new" units:
Length 1 car = 20 feet [ft]
Ti...
Thinking Like an Engineer: An Active Learning Approach (3rd Edition)
1.1 What is the difference between an atom and a molecule? A molecule and a crystal?
Manufacturing Engineering & Technology
Name three purposes that a resist mask can play.
DeGarmo's Materials and Processes in Manufacturing
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, mechanical-engineering and related others by exploring similar questions and additional content below.Similar questions
- Help me understand by teaching me the solution. Thanks i upvote.arrow_forwardA solid bar of length L = 4 m and diameter 100 mm is heated from 20 to 400 degrees celsius and restrained between two solid immovable walls. Young's modulus of the material is 95 GPa and the coefficient of thermal expansion is 23 x 10-6/°C. Calculate the thermal strain, e, in micro-strain correct to two decimal places. Calculate the thermal stress, o, in megapascals (MPa) correct to two decimal places. MPa. E: σ: micro-strain. Hence calculate the force exerted by the bar in meganewtons (MN) correct to two decimal places: F MN. Larrow_forwardFigure Q1(b) shows three rods that were assembled together and held between rigid supports. The material properties of each material are given in Table Q1(b). Suppose the initial temperature is T1 = 2x °C. The temperature then raised up and reaches T2 = 7y oC, Parameter x and y are given by X=0 Y=0 i) Calculate the average normal stress in each material when the temperature reaches T2. ii) Determine the corresponding displacement at point A. Brass Copper Steel |A |B .600 mm .400 mm 200 mm Figure Q1(b) Table Q1(b) Steel Brass Сopper 120 GPa E 200GPA 100 GPa 12×10-/ °C 21×10/ °C 17×10/ °C a d 16mm 24 mm 26 mmarrow_forward
- What’s the answer for this please ?arrow_forwardStrength of materials w/solutionarrow_forwardA solid bar of length L = 2 m and diameter 50 mm is heated from 20 to 350 degrees celsius and restrained between two solid immovable walls. L Young's modulus of the material is 80 GPa and the coefficient of thermal expansion is 23 × 10 6/ºC. Calculate the thermal strain, e, in micro-strain correct to two decimal places. micro-strain. Calculate the thermal stress, o, in megapascals (MPa) correct to two decimal places. MPа. Hence calculate the force exerted by the bar in meganewtons (MN) correct to two decimal places: F: MN.arrow_forward
- Please show a step by step solution thankyouarrow_forwardStrength of Materialsarrow_forward2. A thin steel tire is shrunk on to a locomotive wheel of 1.2 m diameter. Find the internal diameter of the tire if after shrinking on, the hoop stress in the tire is 100 MPa. Assume E=200kN/mm2. Also find the least temperature to which the tire must be heated above that of the wheel before it could be slipped on. The coefficient of linear expansion for the tire is 6.5×10–6 per °C.arrow_forward
- A prismatic bar at 10 degrees celsius in a rigid conrete wall at both ends. The bar is 1000 mm long and has a cross-sectional area of 2600mm^2. What is most nearly the axial force in the bar if the temperature is raised at 40 to degrees celsius?arrow_forwardTopic: Mechanics of Deformable Bodies: Stress and Deformation Direction: Answer with complete solution.arrow_forward1.4-7 The data shown in the table below were obtained from a tensile test of high-strength steel. The test specimen had a diameter of 13 mm and a gage length of 50 mm (see figure for Prob. 1.4-3). At fracture, the elongation between the gage marks was 3.0 mm and the minimum diameter was 10.7 mm. Plot the conventional stress-strain curve for the steefor the steel and determine the proportional limit, modulus of elastics of elastic- ity (i.e., the slope of the initial part of the stress-strain,tress-strain curve), yield stress at 0.1% offset, ultimate stress, percent, elongation in 50 mm, and percent reduction in area. 'ess, percent area. TENSILE-TEST DATA FOR PROB. 1.4-7 Elongation (mm) 0.005 0.015 0.048 Load (kN) 5 10 30 50 0.084 60 0.099 64.5 0.109 67.0 0.119 68.0 0.137 69.0 0.160 70.0 0.229 72.0 0.259 76.0 0.330 84.0 0.584 92.0 0.853 100.0 1.288 112.0 2.814 113.0 Fracturearrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning
Principles of Heat Transfer (Activate Learning wi...Mechanical EngineeringISBN:9781305387102Author:Kreith, Frank; Manglik, Raj M.Publisher:Cengage Learning
Mechanics of Materials (MindTap Course List)
Mechanical Engineering
ISBN:9781337093347
Author:Barry J. Goodno, James M. Gere
Publisher:Cengage Learning
Principles of Heat Transfer (Activate Learning wi...
Mechanical Engineering
ISBN:9781305387102
Author:Kreith, Frank; Manglik, Raj M.
Publisher:Cengage Learning
Material Science, Phase Diagrams, Part 1; Author: Welt der Werkstoffe;https://www.youtube.com/watch?v=G83ZaoB3XCc;License: Standard Youtube License