Chapter 1, Problem 21E

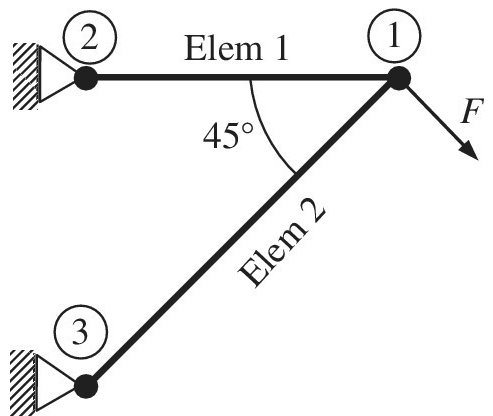
The truss structure shown in the figure supports a force F. The finite element method is used to analyze this structure using two truss elements as shown in the figure. The cross- sectional area for both elements is $\text{A}={\text{2 in}}^{\text{2}}$, and the lengths are ${\text{L}}^{(\text{2})}=\text{1}0\text{ ft}$. Young’s Modulus of the material $\text{E}=\text{3}0\times {10}^{\text{6}}\text{psi}$.

a. Compute the transformation matrix [T] for element 2 that enables you to transform between global and local coordinates (as shown in equation below).

$\left\{\begin{array}{l}\overline{u_1}\\ \overline{u_2}\end{array}\right\}=\left[T\right]\left\{\begin{array}{l}{u}_1\\ v_1\\ u_3\\ v_3\end{array}\right\}$

b. It is determined after solving the final equations that the displacement components of the node 1 are: ${\text{u}}_{\text{5}}=0.\text{5}\times \text{1}{0}^{-\text{2}}\text{in}$. and ${\text{v}}_{\text{1}}=-\text{1}.\text{5}\times \text{1}{0}^{-\text{2}}\text{in}$. What are the strain, stress, and force in element 2?