
Concept explainers
A particle moves in the xy plane (Fig. P9.30) from the origin to a point having coordinates x = 7.00 m and y = 4.00 m under the influence of a force given by →F=3y2î+x�.
- a. What is the work done on the particle by the force F if it moves along path 1 (shown in red)?
- b. What is the work done on the particle by the force F if it moves along path 2 (shown in blue)?
- c. What is the work done on the particle by the force F if it moves along path 3 (shown in green)?
- d. Is the force F conservative or nonconservative? Explain.
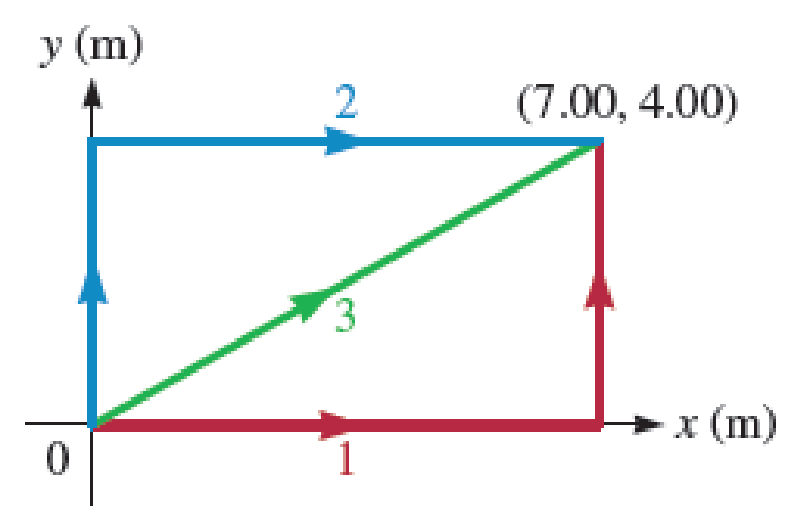
FIGURE P9.30
In each case, the work is found using the integral of →F·d→r along the path (Equation 9.21).
W=∫rfrt→F·d→r=∫rfrt(Fxdx+Fydy+Fzdz)
(a) The work done along path 1, we first need to integrate along d→r=dxˆi from (0,0) to (7,0) and then along d→r=dyˆj from (7,0) to (7,4):
W1=x=7;y=0∫x=0;y=0(3y2ˆi+xˆj)·(dxˆi)+x=7;y=4∫x=7;y=0(3y2ˆi+xˆj)·(dyˆj)
Performing the dot products, we get
W1=x=7;y=0∫x=0;y=03y2dx+x=7;y=4∫x=7;y=0xdy
Along the first part of this path, y = 0 therefore the first integral equals zero. For the second integral, x is constant and can be pulled out of the integral, and we can evaluate dy.
W1=0+x=7;y=4∫x=7;y=0xdy=xy|x=7;y=4x=7;y=0=28 J
(b) The work done along path 2 is along d→r=dyˆj from (0,0) to (0,4) and then along d→r=dxˆi from (0,4) to (7,4):
W2=x=0;y=4∫x=0;y=0(3y2ˆi+xˆj)·(dyˆj)+x=7;y=4∫x=0;y=4(3y2ˆi+xˆj)·(dyˆi)
Performing the dot product, we get:
W2=x=0;y=4∫x=0;y=0xdy+x=7;y=4∫x=0;y=43y2dx
Along the first part of this path, x = 0. Therefore, the first integral equals zero. For the second integral, y is constant and can be pulled out of the integral, and we can evaluate dx.
W2=0+3y2x|x=7;y=4x=0;y=4=336 J
(c) To find the work along the third path, we first write the expression for the work integral.
W=∫rfrt→F·d→r=∫rfrt(Fxdx+Fydy+Fzdz)W=∫rfrt(3y2dx+x dy) (1)
At first glance, this appears quite simple, but we can’t integrate ∫xdy=xy like we might have above because the value of x changes as we vary y (i.e., x is a function of y.) [In parts (a) and (b), on a straight horizontal or vertical line, only x or y changes]. One approach is to parameterize both x and y as a function of another variable, say t, and write each integral in terms of only x or y. Constraining dr to be along the desired line, we can relate dx and dy:
tanθ=dydxdy=tanθdx and dx=dytanθ (2)
Now, use equation (2) in (1) to express each integral in terms of only one variable.
W=x=7;y=4∫x=0;y=03y2dx+x=7;y=4∫x=0;y=0x dyW=y=4∫y=03y2dytanθ+x=7∫x=0x tanθ dx
We can determine the tangent of the angle, which is constant (the angle is the angle of the line with respect to the horizontal).
tanθ=4.007.00=0.570
Insert the value of the tangent and solve the integrals.
W=30.570y33|y=4y=0+0.570x22|x=7x=0W=112+14=126 J
(d) Since the work done is not “path-independent”, this is non-conservative force.
Figure P9.30ANS
(a)
The work done on the particle by the force F if it moves along the path 1.
Answer to Problem 30PQ
The work done on the particle by the force F if it moves along the path 1 is 28 J_.
Explanation of Solution
The path 1 followed by the particle is given in Figure P9.30. Given that the coordinate of the final position of the particle is (7.00, 4.00) and the force is →F=3y2ˆi+xˆj.
Write the expression for the work done by a force.
W=rf∫ri→F⋅d→r (I)
Here, W is the work done, rf is the final position, ri is the initial position, and d→r is the elemental path.
The path 1 of the particle consist of two parts. Motion from (0, 0) to (7, 0) and (7, 0) to (7, 4). Thus, the integration has to be performed along d→r=dxˆi from (0, 0) to (7, 0) and then along d→r=dyˆj from (7, 0) to (7, 4).
Use the force vector along with the limits of integration and perform the integration (represent the work done along path 1 as W1).
W1=x=7;y=0∫x=0;y=0(3y2ˆi+xˆj)·(dxˆi)+x=7;y=4∫x=7;y=0(3y2ˆi+xˆj)·(dyˆj) (II)
Perform the dot product to reduce the integral (II).
W1=x=7;y=0∫x=0;y=03y2dx+x=7;y=4∫x=7;y=0xdy (III)
Along the first part of the path 1, y=0, and hence the first integral equals zero. For the second integral, x is constant and can be pulled out of the integral, and dy can be evaluated.
W1=0+x=7;y=4∫x=7;y=0xdy=xy|x=7;y=4x=7;y=0=28−0=28 J
Conclusion:
Therefore, the work done on the particle by the force F if it moves along the path 1 is 28 J_.
(b)
The work done on the particle by the force F if it moves along the path 2.
Answer to Problem 30PQ
The work done on the particle by the force F if it moves along the path 2 is 336 J_.
Explanation of Solution
The path 2 followed by the particle is given in Figure P9.30. Given that the coordinate of the final position of the particle is (7.00, 4.00) and the force is →F=3y2ˆi+xˆj.
Equation (I) gives the expression for the work done by a force.
W=rf∫ri→F⋅d→r
The path 2 of the particle consist of two parts. Motion from (0, 0) to (0, 4) and (0, 4) to (7, 4). Thus, the integration has to be performed along d→r=dyˆj from (0, 0) to (0, 4) and then along d→r=dxˆi from (0, 4) to (7, 4).
Use the force vector along with the limits of integration and perform the integration (represent the work done along path 2 as W2).
W2=x=0;y=4∫x=0;y=0(3y2ˆi+xˆj)·(dyˆj)+x=7;y=4∫x=0;y=4(3y2ˆi+xˆj)·(dxˆi) (IV)
Perform the dot product to reduce the integral (IV).
W2=x=0;y=4∫x=0;y=0xdy+x=7;y=4∫x=0;y=43y2dx (V)
Along the first part of the path 2, x=0, and hence the first integral equals zero. For the second integral, y is constant and can be pulled out of the integral, and dx can be evaluated.
W2=0+x=7;y=4∫x=0;y=43y2dx=3y2x|x=7;y=4x=0;y=4=336−0=336 J
Conclusion:
Therefore, the work done on the particle by the force F if it moves along the path 2 is 336 J_.
(c)
The work done on the particle by the force F if it moves along the path 3.
Answer to Problem 30PQ
The work done on the particle by the force F if it moves along the path 3 is 126 J_.
Explanation of Solution
The path 3 followed by the particle is given in Figure P9.30. Given that the coordinate of the final position of the particle is (7.00, 4.00) and the force is →F=3y2ˆi+xˆj.
Equation (I) gives the expression for the work done by a force.
W=rf∫ri→F⋅d→r
Write equation (I) in terms of x, y, and z components.
W=rf∫ri(Fxdx+Fydy+Fzdz) (VI)
Use the x and y components of the given force in the integral (VI). Since the motion is confined in xy plane, there is no z component in the integral.
W=rf∫ri(3y2dx+xdy) (VII)
The path 3 of the particle starts from (0, 0) and ends at (7, 4). Thus, the integral (VII) can be written as (represent the work done along path 3 as W3),
W3=x=7;y=4∫x=0;y=03y2dx+x=7;y=4∫x=0;y=0xdy (VIII)
Here, both x and y coordinates change and hence direct integration cannot be performed. Let us consider the angle θ that the vector of path 3 make with the x axis as shown in Figure 1.
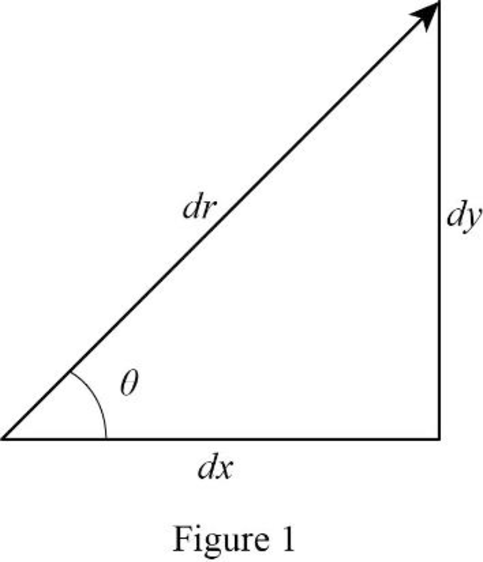
Write the expression relating dx, dy, and θ.
tanθ=dydx (IX)
Solve equation (IX) for dy.
dy=tanθdx (X)
Solve equation (IX) for dx.
dx=dytanθ (XI)
Use equation (X) and (XI) in (VIII).
W3=x=7;y=4∫x=0;y=03y2dytanθ+x=7;y=4∫x=0;y=0xtanθdx (XII)
Compute tanθ from the paths shown in Figure P9.30.
tanθ=4.007.00=0.570 (XIII)
Use equation (XIII) in (XII) and perform the integral.
W3=y=4∫y=030.570y2dy+x=7∫x=00.570xdx=30.570y33|y=4y=0+0.570x22|x=7x=0=112+14=126 J
Conclusion:
Therefore, the work done on the particle by the force F if it moves along the path 3 is 126 J_.
(d)
Whether the force →F is conservative or non-conservative.
Answer to Problem 30PQ
The force →F is non-conservative in nature.
Explanation of Solution
From part (a), (b) and (c) it is found that the work done by the force →F on moving the particle from (0,0) to (7, 4) along different path is different. By the definition of conservative forces, the work done by a conservative force is path independent. However, here the work done by the force →F is path dependent and hence it is a non-conservative force.
Conclusion:
Therefore, the force →F is non-conservative in nature.
Want to see more full solutions like this?
Chapter 9 Solutions
Physics for Scientists and Engineers: Foundations and Connections
- Question 16 2.9 Three Pulleys 2.9a A thin, light rope is draped over three frictionless pulleys arranged around the origin as shown. Each pulley is a solid disk of radius r=2cm and is equidistant from the origin. 5kg mass is attached to one side and a 7kg mass to the other. Before the masses are released and in motion, what is the total angular momentum in kgm2/s around the origin? Question 17 2.9b What fraction of the angular momentum is in the pulleys?arrow_forwardAt what temperature would water boil if the outside pressure was only 19,900 Pa in degrees Celsius?arrow_forwardWhich of these properties of a sound wave is associated with the pitch of the sound that we hear? amplitudefrequency intensity levelintensityarrow_forward
- A wave travels upward in a medium (vertical wave velocity). What is the direction of particle oscillation for the following? (a) a longitudinal wave parallel to the direction of propagationperpendicular to the direction of propagationarrow_forwardThe faster a molecule is moving in the upper atmosphere, the more likely it is to escape Earth's gravity. Given this fact, and your knowledge of rms speed, which of the following molecules can escape most easily from Earth's atmosphere if they are all at the same temperature?arrow_forwardThe temperature in one part of a flame is 2,100 K. What is the rms velocity of the carbon dioxide molecules at this temperature? Give your answer as the number of meters per second. mass of 1 mole of CO2 = 44.0 grams 1 mole contains 6.02 x 1023 molecules the Boltzmann constant k = 1.38 x 10-23 J/Karrow_forward
- The specific heat of a certain substance is 375 J/(kg°C). How much heat energy would you have to add to increase the temperature of 22 kg of this substance from 33°C up to 44°C in a number of Joules?arrow_forward3.9 moles of an ideal gas are sealed in a container with volume 0.22 m3, at a pressure of 146,000 N/m2. What is the temperature of the gas in degrees Celsius?arrow_forwardwhen a cannon is launched at a 65 degree angle, will it have the same horizontal velocity as when it is launched from a 25 degree angle as long as the initial speed is the same?arrow_forward
 Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning
Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Physics for Scientists and Engineers, Technology ...PhysicsISBN:9781305116399Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers, Technology ...PhysicsISBN:9781305116399Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning College PhysicsPhysicsISBN:9781938168000Author:Paul Peter Urone, Roger HinrichsPublisher:OpenStax College
College PhysicsPhysicsISBN:9781938168000Author:Paul Peter Urone, Roger HinrichsPublisher:OpenStax College





