
a.
To express
a.
Answer to Problem 9CE
Explanation of Solution
Given:
Three
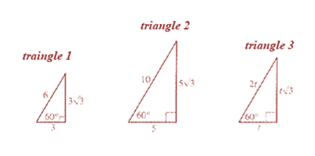
Formula used:
In triangle 1:
In triangle 2:
In triangle 3:
Conclusion:
Therefore, the simplest radical form of
b.
To find the appropriate value for
b.
Answer to Problem 9CE
The approximate value of
Explanation of Solution
Given:
Three
Calculation:
Conclusion:
Therefore, the approximate value of
c.
To check whether the value of
c.
Answer to Problem 9CE
Correct
Explanation of Solution
Given: Three
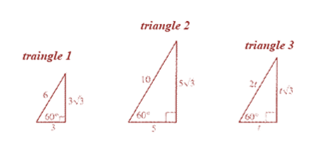
From above sub parts,
Value of
Calculation:
From above sub parts, the value of
Rounding it to 4 decimal places,
The value of
Here, both values are equal to each other.
Conclusion:
Therefore, the given value is correct.
Chapter 8 Solutions
McDougal Littell Jurgensen Geometry: Student Edition Geometry
Additional Math Textbook Solutions
Basic Business Statistics, Student Value Edition
University Calculus: Early Transcendentals (4th Edition)
Calculus: Early Transcendentals (2nd Edition)
Pre-Algebra Student Edition
Introductory Statistics
A Problem Solving Approach To Mathematics For Elementary School Teachers (13th Edition)
- In quadrilateral QRST, m<R=60, m<T=90, QR=RS, ST=8, TQ=8 How long is the longer diagonal of QRST? Find the ratio of RT to QS.arrow_forward13:26 ... ← Robert F. Blitzer - Thinkin... 0,04 61 KB/d 目 polygons to create a fraudulent tessellation with discrepancies that are too subtle for the eye to notice. In Exercises 45-46, you will use mathematics, not your eyes, to observe the irregularities. B A 45. Find the sum of the angle measures at vertex A. Then explain why the tessellation is a fake. 46. Find the sum of the angle measures at vertex B. Then explain why the tessellation is a fake. =et at If se Fic SECTION 10.3 Polygons, Perimeter, and Tessellations 645 61. I find it helpful to think of a polygon's perimeter as the length of its boundary. 62. If a polygon is not regular, I can determine the sum of the measures of its angles, but not the measure of any one of its angles. 63. I used floor tiles in the shape of regular pentagons to completely cover my kitchen floor. In Exercises 64-65, write an algebraic expression that represents the perimeter of the figure shown. is be 64. le a b C 2/ If se nyarrow_forwardSchoology → C Cportsk12.com bookmarks Sis Grades and Attendance Al Detector - the Original Al Che X GPTZero + portsmouth.schoology.com/common-assessment-delivery/start/7747152192?action=onresume&submissionId=1600790102 New Tab Home | Schoology Quadrilateral Quiz English If WXYZ is a square, and WY = 32, find XY. Round your answer to the nearest tenth. Z XY = R X Y POSSIBLE POINTS: 5 2 of 20 48 21 1 2 345678910 Next ▸ Δ ㄖㄨ All Bookmarks Schoology Help Center | PRIVACY POLICY | Terms of Use PowerSchool ©2025arrow_forward
- om nearest tenth if necessary. milsum 3. છે. 9.3mm 3mm A 78-43-92 4-3) 11.7 of 72.04-11.7-= lygons 7.8 mi 60.94 blants" 9 om 6. 4.15-7 16- 32m 1.8m 4.5m % ose 4.5m as to 65m 14 represents 5 square meters.arrow_forwardThe diagonals of rhombus ABCD intersect at E. Given that BAC=53 degrees, DE=8, and EC=6 find AEarrow_forwardVolume of Dubai Cayan Towerarrow_forward
- 1 B-P P+1+ 2-p 4-p min(Red)=? y=x² A (P,P')arrow_forwardMI P X /courses/segura10706/products/171960/pages/611?locale=&platformId=1030&lms=Y ☆ Finish Part I: Mathematics for Elementary and Middle School Teachers Continue in the app JJ 576 Chapter 12. Area of Shapes 9. Determine the area of the shaded shapes in Figure 12.48. Explain your reasoning. 1 unit S Figure 12.48 1 unit unit and the yarn for thearrow_forwardChrom ESS $425 5. Ar Dive for x 21) Name 1. Classify the triangles based on their side lengths and angle measures. 89° 30° Acute Scalene Right Scalene 130° Date A +100 Obtuse Equiangular Isosceles Equilateral What additional information would you need to prove these triangles congruent by ASA? If marrow_forwardBoth find out Only 100% sure experts solve it correct complete solutions okkk don't use chat gpt or other ai okkarrow_forwardOnly 100% sure experts solve it correct complete solutions okkk don't use chat gpt or other ai okkarrow_forwardLogin HAC Home View Summary MwMerriam-Webster: A... Lizard Point Quizze... G Home | Gimkit Quizlet Live | Quizlet K! Kahoot! 7.2 HW Central Angles, Arcs, and Arc Lengths POSSIBLE POINTS: 6.67 11. If myQ=(y+7), mQR = (x+11), mRS = (3y), and mST = 65°, find the values of x and y. R V X = y = W S T q W a It N S C % 65 54 # m d DELL 96 t y 0 27 & J * 00 8 x= y= f g h J k X C V b n 3 ES 1 Feb 26 alt ctrlarrow_forwardarrow_back_iosSEE MORE QUESTIONSarrow_forward_ios
 Elementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage,
Elementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage, Elementary Geometry for College StudentsGeometryISBN:9781285195698Author:Daniel C. Alexander, Geralyn M. KoeberleinPublisher:Cengage Learning
Elementary Geometry for College StudentsGeometryISBN:9781285195698Author:Daniel C. Alexander, Geralyn M. KoeberleinPublisher:Cengage Learning

