Chapter 8, Problem 8CR

To determine

To calculate: the length of the base of an isosceles triangle.

Answer to Problem 8CR

The length of base of an isosceles triangle is $12$

Explanation of Solution

Given Information: The legs of an isosceles triangle are 10 units long and altitude to the base is 8 units long.

Formula used:

Formula used:

The relationship between the legs of right triangle (shown in figure below) a , b and its hypotenuse c is obtained by using Pythagoras theorem.

  

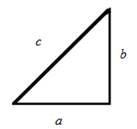
It can be expressed as,

  $\begin{array}{l}{c}^2=a^2+b^2\\ c=\sqrt{a^2+b^2}\end{array}$

Calculation: Consider the isosceles triangle given below.

  

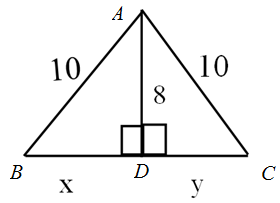
Here, two right triangles are formed with in the isosceles triangle as shown in the above Figure. Here, one of the smaller triangles can be considered and Pythagoras theorem can be applied on them to calculate x or y .Since the triangle is isosceles, the total base length can be obtained as twice one of these two lengths.

Considering the ΔADB, the Pythagoras theorem gives,

  $\begin{array}{c}{10}^2=\sqrt{x^2+8^2}\\ x^2=\sqrt{{10}^2-8^2}\\ =\sqrt{36}\\ =6\end{array}$

Now, the length of the base is given by,

  $\begin{array}{c}BC=2x\\ =2\times 6\\ =12\end{array}$