Chapter 6, Problem 6.19P

(a)

To determine

The tangent elastic modulus.

Answer to Problem 6.19P

The tangent elastic modulus at zero strain is $1.2\times {10}^9\text{Pa}$ .

Explanation of Solution

Formula Used:

Write the expression for the tangent elastic modulus.

  $E_0=\frac{\Delta \sigma }{\Delta \epsilon }$ …… (I)

Here, $E_0$ is the tangent elastic modulus at 0 strain, $\Delta \sigma$ is the change in stress and $\Delta \epsilon$ is the change in strain.

Calculation:

Refer Figure 6.16 “Tensile stress-strain diagram for four different type of materials” from the book “Material Science and Engineering Properties”.

The value of change is stress for PMMA is $\Delta \sigma =6\times {10}^7\text{Pa}$ and change in strain for PMMA is $0.05$ .

Substitute $6\times {10}^7\text{Pa}$ for $\Delta \sigma$ and $0.05$ for $\Delta \epsilon$ in equation (I).

  $\begin{array}{c}{E}_0=\frac{6\times {10}^7\text{Pa}}{0.05}\\ =120\times {10}^7\text{Pa}\\ =1.2\times {10}^9\text{Pa}\end{array}$

Conclusion:

Thus, the tangent elastic modulus at zero strain is $1.2\times {10}^9\text{Pa}$ .

(b)

To determine

The yield stress of PMMA.

Answer to Problem 6.19P

The yield stress for PMMA is $2.7\times {10}^7\text{Pa}$ .

Explanation of Solution

Calculation:

Refer Figure 6.16 “Tensile stress-strain diagram for four different type of materials” from the book “Material Science and Engineering Properties”.

The tensile stress diagram for PMMA is shown in figure below.

  

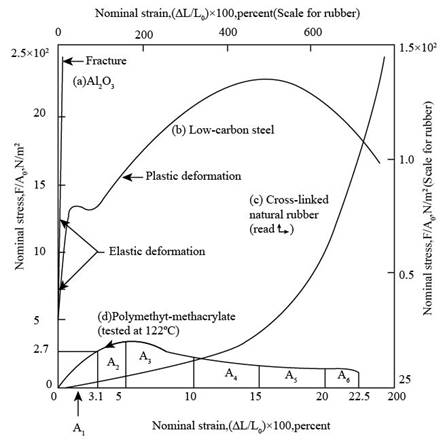
Figure (1)

The value of the yield stress for PMMA is $2.7\times {10}^7\text{Pa}$ .

Conclusion:

Thus, the yield stress for PMMA is $2.7\times {10}^7\text{Pa}$ .

(c)

To determine

The resilience of PMMA.

Answer to Problem 6.19P

The resilience of PMMA is $3.03\times {10}^5\text{J}/{\text{m}}^{\text{3}}$ .

Explanation of Solution

Formula Used:

Write the expression for the resilience.

  $R=\frac{{\sigma }_{\text{y}}^2}{2E}$ …… (II)

Here, $R$ is the resilience, ${\sigma }_{\text{y}}$ is the yield stress and $E$ is the Young’s modulus.

Calculation:

Substitute $2.7\times {10}^7\text{Pa}$ for ${\sigma }_{\text{y}}$ and $1.2\times {10}^9\text{Pa}$ for $E$ in equation (II).

  $\begin{array}{c}R=\frac{{\left(2.7\times {10}^7\text{Pa}\right)}^2}{2\left(1.2\times {10}^9\text{Pa}\right)}\\ =\frac{7.29\times {10}^{14}{\text{Pa}}^2}{2.4\times {10}^9\text{Pa}}\\ =\left(\left(3.03\times {10}^5\text{Pa}\right)\left(\frac{1\text{J}/{\text{m}}^{\text{3}}}{1\text{Pa}}\right)\right)\\ =3.03\times {10}^5\text{J}/{\text{m}}^{\text{3}}\end{array}$

Conclusion:

Thus, the resilience of PMMA is $3.03\times {10}^5\text{J}/{\text{m}}^{\text{3}}$ .

(d)

To determine

The ultimate tensile strength of PMMA.

Answer to Problem 6.19P

The ultimate tensile strength for PMMA is $3.5\times {10}^7\text{Pa}$ .

Explanation of Solution

Calculation:

The ultimate tensile strength in a stress-strain diagram is obtained by observation of the highest point that is reached by the curve after which the necking of curve starts.

Refer Figure 6.16 “Tensile stress-strain diagram for four different type of materials” from the book “Material Science and Engineering Properties”.

The value of the ultimate tensile strength for PMMA is $3.5\times {10}^7\text{Pa}$ .

Conclusion:

Thus, the ultimate tensile strength for PMMA is $3.5\times {10}^7\text{Pa}$ .

(e)

To determine

The toughness of PMMA.

Answer to Problem 6.19P

The toughness of PMMA is $4.3\times {10}^6\text{J}/{\text{m}}^{\text{3}}$ .

Explanation of Solution

Formula Used:

Write the expression for the first area.

  $A_1=R$ …… (III)

Here, $A_1$ is the first area.

Write the expression for the second area.

  $A_2=\left(0.05-0.031\right)\left(\frac{{\sigma }_{\text{y}}+{\sigma }_{\text{y2}}}{2}\right)$ …… (IV)

Here, $A_2$ is the second area , ${\sigma }_{\text{y2}}$ are the yield stresses for second area.

Write the expression for the third area.

  $A_3=\left(0.1-0.05\right)\left(\frac{{\sigma }_{\text{y2}}+{\sigma }_{\text{y3}}}{2}\right)$ …… (V)

Here, $A_3$ is the third area, ${\sigma }_{\text{y3}}$ are the yield stresses for third area.

Write the expression for the fourth area.

  $A_4=\left(0.15-0.1\right)\left(\frac{{\sigma }_{\text{y3}}+{\sigma }_{\text{y4}}}{2}\right)$ …… (VI)

Here, $A_4$ is the fourth area, ${\sigma }_{\text{y4}}$ are the yield stresses for fourth area.

Write the expression for the fifth area.

  $A_5=\left(0.2-0.15\right)\left(\frac{{\sigma }_{\text{y4}}+{\sigma }_{\text{y5}}}{2}\right)$ …… (VII)

Here, $A_5$ is the fifth area, ${\sigma }_{\text{y5}}$ are the yield stresses for fifth area.

Write the expression for the sixth area.

  $A_6=\left(0.225-0.20\right)\left(\frac{{\sigma }_{\text{y5}}+{\sigma }_{\text{y6}}}{2}\right)$ …… (VIII)

Here, $A_6$ is the sixth area, ${\sigma }_{\text{y6}}$ are the yield stresses for sixth area.

Write the expression for the toughness of specimen.

  $\text{Toughness}=A_1+A_2+A_3+A_4+A_5+A_6$ …… (IX)

Calculation:

Refer Figure 6.16 “Tensile stress-strain diagram for four different type of materials” from the book “Material Science and Engineering Properties”.

The stress strain diagram for PMMA with sub-divided area is shown below,

  

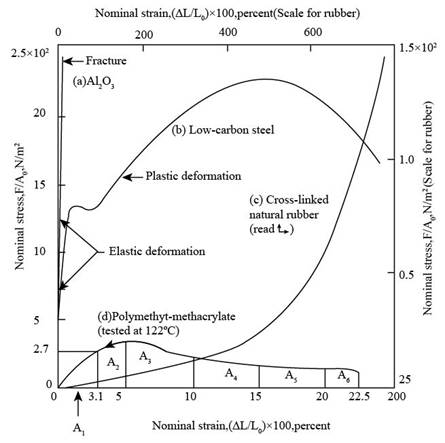
Figure (2)

Substitute $3.03\times {10}^5\text{J}/{\text{m}}^{\text{3}}$ for $R$ in equation (III).

  $\begin{array}{c}{A}_1=3.03\times {10}^5\text{J}/{\text{m}}^{\text{3}}\\ =0.3\times {10}^6\text{J}/{\text{m}}^{\text{3}}\end{array}$

Substitute $27\text{MPa}$ for ${\sigma }_{\text{y}}$ and $34\text{MPa}$ for ${\sigma }_{\text{y2}}$ in equation (IV).

  $\begin{array}{c}{A}_2=\left(0.05-0.031\right)\left(\frac{\left(\left(27\text{MPa}\right)\left(\frac{{10}^6\text{Pa}}{1\text{MPa}}\right)\right)+\left(\left(34\text{MPa}\right)\left(\frac{{10}^6\text{Pa}}{1\text{MPa}}\right)\right)}{2}\right)\\ =\left(0.019\right)\left(\frac{\left(61\times {10}^6\text{Pa}\right)}{2}\right)\\ =\left(\left(0.6\times {10}^6\text{Pa}\right)\left(\frac{1\text{J}/{\text{m}}^{\text{3}}}{1\text{Pa}}\right)\right)\\ =0.6\times {10}^6\text{J}/{\text{m}}^{\text{3}}\end{array}$

Substitute $22\text{MPa}$ for ${\sigma }_{\text{y3}}$ and $34\text{MPa}$ for ${\sigma }_{\text{y2}}$ in equation (V).

  $\begin{array}{c}{A}_3=\left(0.1-0.05\right)\left(\frac{\left(\left(34\text{MPa}\right)\left(\frac{{10}^6\text{Pa}}{1\text{MPa}}\right)\right)+\left(\left(22\text{MPa}\right)\left(\frac{{10}^6\text{Pa}}{1\text{MPa}}\right)\right)}{2}\right)\\ =\left(0.05\right)\left(\frac{\left(56\times {10}^6\text{Pa}\right)}{2}\right)\\ =\left(\left(1.4\times {10}^6\text{Pa}\right)\left(\frac{1\text{J}/{\text{m}}^{\text{3}}}{1\text{Pa}}\right)\right)\\ =1.4\times {10}^6\text{J}/{\text{m}}^{\text{3}}\end{array}$

Substitute $22\text{MPa}$ for ${\sigma }_{\text{y3}}$ and $16\text{MPa}$ for ${\sigma }_{\text{y4}}$ in equation (VI).

  $\begin{array}{c}{A}_4=\left(0.15-0.1\right)\left(\frac{\left(\left(22\text{MPa}\right)\left(\frac{{10}^6\text{Pa}}{1\text{MPa}}\right)\right)+\left(\left(16\text{MPa}\right)\left(\frac{{10}^6\text{Pa}}{1\text{MPa}}\right)\right)}{2}\right)\\ =\left(0.05\right)\left(\frac{\left(38\times {10}^6\text{Pa}\right)}{2}\right)\\ =\left(\left(0.95\times {10}^6\text{Pa}\right)\left(\frac{1\text{J}/{\text{m}}^{\text{3}}}{1\text{Pa}}\right)\right)\\ =0.95\times {10}^6\text{J}/{\text{m}}^{\text{3}}\end{array}$

Substitute $14\text{MPa}$ for ${\sigma }_{\text{y5}}$ and $16\text{MPa}$ for ${\sigma }_{\text{y4}}$ in equation (VII).

  $\begin{array}{c}{A}_5=\left(0.2-0.15\right)\left(\frac{\left(\left(16\text{MPa}\right)\left(\frac{{10}^6\text{Pa}}{1\text{MPa}}\right)\right)+\left(\left(14\text{MPa}\right)\left(\frac{{10}^6\text{Pa}}{1\text{MPa}}\right)\right)}{2}\right)\\ =\left(0.05\right)\left(\frac{\left(30\times {10}^6\text{Pa}\right)}{2}\right)\\ =\left(\left(0.75\times {10}^6\text{Pa}\right)\left(\frac{1\text{J}/{\text{m}}^{\text{3}}}{1\text{Pa}}\right)\right)\\ =0.75\times {10}^6\text{J}/{\text{m}}^{\text{3}}\end{array}$

Substitute $14\text{MPa}$ for ${\sigma }_{\text{y5}}$ and $10\text{MPa}$ for ${\sigma }_{\text{y6}}$ in equation (VIII).

  $\begin{array}{c}{A}_6=\left(0.225-0.20\right)\left(\frac{\left(\left(14\text{MPa}\right)\left(\frac{{10}^6\text{Pa}}{1\text{MPa}}\right)\right)+\left(\left(10\text{MPa}\right)\left(\frac{{10}^6\text{Pa}}{1\text{MPa}}\right)\right)}{2}\right)\\ =\left(0.025\right)\left(\frac{\left(24\times {10}^6\text{Pa}\right)}{2}\right)\\ =\left(\left(0.3\times {10}^6\text{Pa}\right)\left(\frac{1\text{J}/{\text{m}}^{\text{3}}}{1\text{Pa}}\right)\right)\\ =0.3\times {10}^6\text{J}/{\text{m}}^{\text{3}}\end{array}$

Substitute $0.3\times {10}^6\text{J}/{\text{m}}^{\text{3}}$ for $A_1$ , $0.6\times {10}^6\text{J}/{\text{m}}^{\text{3}}$ for $A_2$ , $1.4\times {10}^6\text{J}/{\text{m}}^{\text{3}}$ for $A_3$ , $0.95\times {10}^6\text{J}/{\text{m}}^{\text{3}}$ for $A_4$ , $0.75\times {10}^6\text{J}/{\text{m}}^{\text{3}}$ for $A_5$ , $0.3\times {10}^6\text{J}/{\text{m}}^{\text{3}}$ for $A_6$ in equation (IX).

  $\begin{array}{c}\text{Toughness}=\left[\begin{array}{l}\left(0.3\times {10}^6\text{J}/{\text{m}}^{\text{3}}\right)+\left(0.6\times {10}^6\text{J}/{\text{m}}^{\text{3}}\right)+\left(1.4\times {10}^6\text{J}/{\text{m}}^{\text{3}}\right)+\left(0.95\times {10}^6\text{J}/{\text{m}}^{\text{3}}\right)\\ +\left(0.75\times {10}^6\text{J}/{\text{m}}^{\text{3}}\right)+\left(0.3\times {10}^6\text{J}/{\text{m}}^{\text{3}}\right)\end{array}\right]\\ =\left(0.3+0.6+1.4+0.95+0.75+0.3\right)\times {10}^6\text{J}/{\text{m}}^{\text{3}}\\ =4.3\times {10}^6\text{J}/{\text{m}}^{\text{3}}\end{array}$

Conclusion:

Thus, the toughness of PMMA is $4.3\times {10}^6\text{J}/{\text{m}}^{\text{3}}$ .