Chapter 6, Problem 6.18P

(a)

To determine

The toughness of $1045$ steel specimen.

Answer to Problem 6.18P

The toughness of $1045$ steel specimen is $80.13\times {10}^6\text{J}/{\text{m}}^{\text{3}}$ .

Explanation of Solution

Formula Used:

Write the expression for the first area.

  $A_1=\frac{{\sigma }_{\text{y}}^2}{2E}$ …… (I)

Here, ${\sigma }_{\text{y}}$ is the yield stress, $A_1$ is the first area and $E$ is the Young’s modulus of the specimen.

Write the expression for the second area.

  $A_2=\left(0.01-{\epsilon }_{\text{y}}\right)\left(\frac{{\sigma }_{\text{y}}+{\sigma }_{\text{y2}}}{2}\right)$ …… (II)

Here, $A_2$ is the second area, ${\epsilon }_{\text{y}}$ is the strain, ${\sigma }_{\text{y2}}$ is the yield stresses for second area.

Write the expression for the third area.

  $A_3=\left(0.01\right)\left(\frac{{\sigma }_{\text{y2}}+{\sigma }_{\text{y3}}}{2}\right)$ …… (III)

Here, $A_3$ is the third area, ${\sigma }_{\text{y3}}$ is the yield stresses for third area.

Write the expression for the fourth area.

  $A_4=\left(0.01\right)\left(\frac{{\sigma }_{\text{y3}}+{\sigma }_{\text{y4}}}{2}\right)$ …… (IV)

Here, $A_4$ is the fourth area, ${\sigma }_{\text{y4}}$ is the yield stresses for fourth area.

Write the expression for the fifth area.

  $A_5=\left(0.01\right)\left(\frac{{\sigma }_{\text{y4}}+{\sigma }_{\text{y5}}}{2}\right)$ …… (V)

Here, $A_5$ is the fifth area, ${\sigma }_{\text{y5}}$ is the yield stresses for fifth area.

Write the expression for the sixth area.

  $A_6=\left(0.01\right)\left(\frac{{\sigma }_{\text{y5}}+{\sigma }_{\text{y6}}}{2}\right)$ …… (VI)

Here, $A_6$ is the sixth area, ${\sigma }_{\text{y6}}$ is the yield stresses for sixth area.

Write the expression for the seventh area.

  $A_7=\left(0.01\right)\left(\frac{{\sigma }_{\text{y6}}+{\sigma }_{\text{y7}}}{2}\right)$ …… (VII)

Here, $A_7$ is the seventh area, ${\sigma }_{\text{y7}}$ is the yield stresses for seventh area.

Write the expression for the eighth area.

  $A_8=\left(0.01\right)\left(\frac{{\sigma }_{\text{y7}}+{\sigma }_{\text{y8}}}{2}\right)$ …… (VIII)

Here, $A_8$ is the eighth area, ${\sigma }_{\text{y8}}$ is the yield stresses for eighth area.

Write the expression for the ninth area.

  $A_9=\left(0.01\right)\left(\frac{{\sigma }_{\text{y8}}+{\sigma }_{\text{y9}}}{2}\right)$ …… (IX)

Here, $A_9$ is the ninth area, ${\sigma }_{\text{y9}}$ is the yield stresses for ninth area.

Write the expression for the tenth area.

  $A_{10}=\left(0.01\right)\left(\frac{{\sigma }_{\text{y9}}+{\sigma }_{\text{y10}}}{2}\right)$ …… (X)

Here, $A_{10}$ is the tenth area, ${\sigma }_{\text{y10}}$ are the yield stresses for tenth area.

Write the expression for the eleventh area.

  $A_{11}=\left(0.008\right)\left(\frac{{\sigma }_{\text{y10}}+{\sigma }_{\text{y11}}}{2}\right)$ …… (XI)

Here, $A_{11}$ is the eleventh area, ${\sigma }_{\text{y11}}$ is the yield stresses for eleventh area.

Write the expression for the toughness of specimen.

  $\text{Toughness}=A_1+A_2+A_3+A_4+A_5+A_6+A_7+A_8+A_9+A_{10}+A_{11}$ …… (XII)

Write the expression for strain at yield point.

  ${\epsilon }_{\text{y}}=\frac{{\sigma }_{\text{y}}}{E}$ …… (XIII)

Calculation:

Refer Figure 6.22 “A true stress-strain diagram for $1045$ steel in mega Pascals $\text{MPa}$ .” of the book “Material Science and Engineering Properties”.

The stress strain diagram for $1045$ steel with sub-divided area is shown below,

  

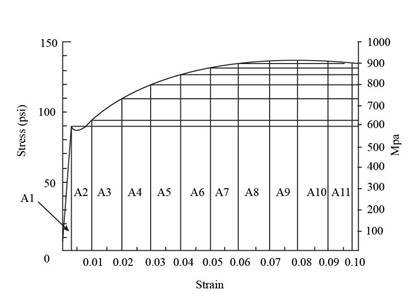
Figure (1)

Substitute $600\text{MPa}$ for ${\sigma }_{\text{y}}$ and $211\text{GPa}$ for $E$ in equation (I).

  $\begin{array}{c}{A}_1=\frac{{\left(\left(600\text{MPa}\right)\left(\frac{{10}^6\text{Pa}}{1\text{MPa}}\right)\right)}^2}{2\left(\left(211\text{Gpa}\right)\left(\frac{{10}^9\text{Pa}}{1\text{MPa}}\right)\right)}\\ =\frac{{\left(600\times {10}^6\text{Pa}\right)}^2}{422\times {10}^9\text{Pa}}\\ =\left(\left(0.85\times {10}^6\text{Pa}\right)\left(\frac{1\text{J}/{\text{m}}^{\text{3}}}{1\text{Pa}}\right)\right)\\ =0.85\times {10}^6\text{J}/{\text{m}}^{\text{3}}\end{array}$

Substitute $600\text{MPa}$ for ${\sigma }_{\text{y}}$ and $211\text{GPa}$ for $E$ in equation (XIII).

  $\begin{array}{c}{\epsilon }_{\text{y}}=\frac{\left(\left(600\text{MPa}\right)\left(\frac{{10}^6\text{Pa}}{1\text{MPa}}\right)\right)}{\left(\left(211\text{Gpa}\right)\left(\frac{{10}^9\text{Pa}}{1\text{MPa}}\right)\right)}\\ =\frac{\left(600\times {10}^6\text{Pa}\right)}{211\times {10}^9\text{Pa}}\\ \approx 0.003\end{array}$

Substitute $600\text{MPa}$ for ${\sigma }_{\text{y}}$ and $620\text{MPa}$ for ${\sigma }_{\text{y2}}$

  $0.003$ for ${\epsilon }_{\text{y}}$ in equation (II).

  $\begin{array}{c}{A}_2=\left(0.01-0.003\right)\left(\frac{\left(\left(600\text{MPa}\right)\left(\frac{{10}^6\text{Pa}}{1\text{MPa}}\right)\right)+\left(\left(620\text{MPa}\right)\left(\frac{{10}^6\text{Pa}}{1\text{MPa}}\right)\right)}{2}\right)\\ =\left(0.007\right)\left(\frac{\left(1220\times {10}^6\text{Pa}\right)}{2}\right)\\ =\left(\left(4.27\times {10}^6\text{Pa}\right)\left(\frac{1\text{J}/{\text{m}}^{\text{3}}}{1\text{Pa}}\right)\right)\\ =4.27\times {10}^6\text{J}/{\text{m}}^{\text{3}}\end{array}$

Substitute $720\text{MPa}$ for ${\sigma }_{\text{y3}}$ and $620\text{MPa}$ for ${\sigma }_{\text{y2}}$ in equation (III).

  $\begin{array}{c}{A}_3=\left(0.01\right)\left(\frac{\left(\left(620\text{MPa}\right)\left(\frac{{10}^6\text{Pa}}{1\text{MPa}}\right)\right)+\left(\left(720\text{MPa}\right)\left(\frac{{10}^6\text{Pa}}{1\text{MPa}}\right)\right)}{2}\right)\\ =\left(0.01\right)\left(\frac{\left(1340\times {10}^6\text{Pa}\right)}{2}\right)\\ =\left(\left(6.7\times {10}^6\text{Pa}\right)\left(\frac{1\text{J}/{\text{m}}^{\text{3}}}{1\text{Pa}}\right)\right)\\ =6.7\times {10}^6\text{J}/{\text{m}}^{\text{3}}\end{array}$

Substitute $720\text{MPa}$ for ${\sigma }_{\text{y3}}$ and $800\text{MPa}$ for ${\sigma }_{\text{y4}}$ in equation (IV).

  $\begin{array}{c}{A}_4=\left(0.01\right)\left(\frac{\left(\left(720\text{MPa}\right)\left(\frac{{10}^6\text{Pa}}{1\text{MPa}}\right)\right)+\left(\left(800\text{MPa}\right)\left(\frac{{10}^6\text{Pa}}{1\text{MPa}}\right)\right)}{2}\right)\\ =\left(0.01\right)\left(\frac{\left(1520\times {10}^6\text{Pa}\right)}{2}\right)\\ =\left(\left(7.6\times {10}^6\text{Pa}\right)\left(\frac{1\text{J}/{\text{m}}^{\text{3}}}{1\text{Pa}}\right)\right)\\ =7.6\times {10}^6\text{J}/{\text{m}}^{\text{3}}\end{array}$

Substitute $860\text{MPa}$ for ${\sigma }_{\text{y5}}$ and $800\text{MPa}$ for ${\sigma }_{\text{y4}}$ in equation (V).

  $\begin{array}{c}{A}_5=\left(0.01\right)\left(\frac{\left(\left(800\text{MPa}\right)\left(\frac{{10}^6\text{Pa}}{1\text{MPa}}\right)\right)+\left(\left(860\text{MPa}\right)\left(\frac{{10}^6\text{Pa}}{1\text{MPa}}\right)\right)}{2}\right)\\ =\left(0.01\right)\left(\frac{\left(1600\times {10}^6\text{Pa}\right)}{2}\right)\\ =\left(\left(8.3\times {10}^6\text{Pa}\right)\left(\frac{1\text{J}/{\text{m}}^{\text{3}}}{1\text{Pa}}\right)\right)\\ =8.3\times {10}^6\text{J}/{\text{m}}^{\text{3}}\end{array}$

Substitute $860\text{MPa}$ for ${\sigma }_{\text{y5}}$ and $880\text{MPa}$ for ${\sigma }_{\text{y6}}$ in equation (VI).

  $\begin{array}{c}{A}_6=\left(0.01\right)\left(\frac{\left(\left(860\text{MPa}\right)\left(\frac{{10}^6\text{Pa}}{1\text{MPa}}\right)\right)+\left(\left(880\text{MPa}\right)\left(\frac{{10}^6\text{Pa}}{1\text{MPa}}\right)\right)}{2}\right)\\ =\left(0.01\right)\left(\frac{\left(1740\times {10}^6\text{Pa}\right)}{2}\right)\\ =\left(\left(8.7\times {10}^6\text{Pa}\right)\left(\frac{1\text{J}/{\text{m}}^{\text{3}}}{1\text{Pa}}\right)\right)\\ =8.7\times {10}^6\text{J}/{\text{m}}^{\text{3}}\end{array}$

Substitute $910\text{MPa}$ for ${\sigma }_{\text{y7}}$ and $880\text{MPa}$ for ${\sigma }_{\text{y6}}$ in equation (VII).

  $\begin{array}{c}{A}_7=\left(0.01\right)\left(\frac{\left(\left(880\text{MPa}\right)\left(\frac{{10}^6\text{Pa}}{1\text{MPa}}\right)\right)+\left(\left(910\text{MPa}\right)\left(\frac{{10}^6\text{Pa}}{1\text{MPa}}\right)\right)}{2}\right)\\ =\left(0.01\right)\left(\frac{\left(1790\times {10}^6\text{Pa}\right)}{2}\right)\\ =\left(\left(8.95\times {10}^6\text{Pa}\right)\left(\frac{1\text{J}/{\text{m}}^{\text{3}}}{1\text{Pa}}\right)\right)\\ =8.95\times {10}^6\text{J}/{\text{m}}^{\text{3}}\end{array}$

Substitute $910\text{MPa}$ for ${\sigma }_{\text{y7}}$ and $920\text{MPa}$ for ${\sigma }_{\text{y8}}$ in equation (VIII).

  $\begin{array}{c}{A}_8=\left(0.01\right)\left(\frac{\left(\left(910\text{MPa}\right)\left(\frac{{10}^6\text{Pa}}{1\text{MPa}}\right)\right)+\left(\left(920\text{MPa}\right)\left(\frac{{10}^6\text{Pa}}{1\text{MPa}}\right)\right)}{2}\right)\\ =\left(0.01\right)\left(\frac{\left(1830\times {10}^6\text{Pa}\right)}{2}\right)\\ =\left(\left(9.15\times {10}^6\text{Pa}\right)\left(\frac{1\text{J}/{\text{m}}^{\text{3}}}{1\text{Pa}}\right)\right)\\ =9.15\times {10}^6\text{J}/{\text{m}}^{\text{3}}\end{array}$

Substitute $910\text{MPa}$ for ${\sigma }_{\text{y9}}$ and $920\text{MPa}$ for ${\sigma }_{\text{y8}}$ in equation (IX).

  $\begin{array}{c}{A}_9=\left(0.01\right)\left(\frac{\left(\left(920\text{MPa}\right)\left(\frac{{10}^6\text{Pa}}{1\text{MPa}}\right)\right)+\left(\left(920\text{MPa}\right)\left(\frac{{10}^6\text{Pa}}{1\text{MPa}}\right)\right)}{2}\right)\\ =\left(0.01\right)\left(\frac{\left(1840\times {10}^6\text{Pa}\right)}{2}\right)\\ =\left(\left(9.20\times {10}^6\text{Pa}\right)\left(\frac{1\text{J}/{\text{m}}^{\text{3}}}{1\text{Pa}}\right)\right)\\ =9.20\times {10}^6\text{J}/{\text{m}}^{\text{3}}\end{array}$

Substitute $920\text{MPa}$ for ${\sigma }_{\text{y9}}$ and $910\text{MPa}$ for ${\sigma }_{\text{y10}}$ in equation (X).

  $\begin{array}{c}{A}_{10}=\left(0.01\right)\left(\frac{\left(\left(920\text{MPa}\right)\left(\frac{{10}^6\text{Pa}}{1\text{MPa}}\right)\right)+\left(\left(910\text{MPa}\right)\left(\frac{{10}^6\text{Pa}}{1\text{MPa}}\right)\right)}{2}\right)\\ =\left(0.01\right)\left(\frac{\left(1830\times {10}^6\text{Pa}\right)}{2}\right)\\ =\left(\left(9.15\times {10}^6\text{Pa}\right)\left(\frac{1\text{J}/{\text{m}}^{\text{3}}}{1\text{Pa}}\right)\right)\\ =9.15\times {10}^6\text{J}/{\text{m}}^{\text{3}}\end{array}$

Substitute $905\text{MPa}$ for ${\sigma }_{\text{y11}}$ and $910\text{MPa}$ for ${\sigma }_{\text{y10}}$ in equation (XI).

  $\begin{array}{c}{A}_{11}=\left(0.008\right)\left(\frac{\left(\left(910\text{MPa}\right)\left(\frac{{10}^6\text{Pa}}{1\text{MPa}}\right)\right)+\left(\left(905\text{MPa}\right)\left(\frac{{10}^6\text{Pa}}{1\text{MPa}}\right)\right)}{2}\right)\\ =\left(0.008\right)\left(\frac{\left(1815\times {10}^6\text{Pa}\right)}{2}\right)\\ =\left(\left(7.26\times {10}^6\text{Pa}\right)\left(\frac{1\text{J}/{\text{m}}^{\text{3}}}{1\text{Pa}}\right)\right)\\ =7.26\times {10}^6\text{J}/{\text{m}}^{\text{3}}\end{array}$

Substitute $0.85\times {10}^6\text{J}/{\text{m}}^{\text{3}}$ for $A_1$ , $4.27\times {10}^6\text{J}/{\text{m}}^{\text{3}}$ for $A_2$ , $6.7\times {10}^6\text{J}/{\text{m}}^{\text{3}}$ for $A_3$ , $7.6\times {10}^6\text{J}/{\text{m}}^{\text{3}}$ for $A_4$ , $8.3\times {10}^6\text{J}/{\text{m}}^{\text{3}}$ for $A_5$ , $8.7\times {10}^6\text{J}/{\text{m}}^{\text{3}}$ for $A_6$ , $8.95\times {10}^6\text{J}/{\text{m}}^{\text{3}}$ for $A_7$ , $9.15\times {10}^6\text{J}/{\text{m}}^{\text{3}}$ for $A_8$ , $9.20\times {10}^6\text{J}/{\text{m}}^{\text{3}}$ for $A_9$ , $9.15\times {10}^6\text{J}/{\text{m}}^{\text{3}}$ for $A_{10}$ , $7.26\times {10}^6\text{J}/{\text{m}}^{\text{3}}$ for $A_{11}$ in equation (XII).

  $\begin{array}{c}\text{Toughness}=\left[\begin{array}{l}\left(0.85\times {10}^6\text{J}/{\text{m}}^{\text{3}}\right)+\left(4.27\times {10}^6\text{J}/{\text{m}}^{\text{3}}\right)+\left(6.7\times {10}^6\text{J}/{\text{m}}^{\text{3}}\right)+\left(7.6\times {10}^6\text{J}/{\text{m}}^{\text{3}}\right)\\ +\left(8.3\times {10}^6\text{J}/{\text{m}}^{\text{3}}\right)+\left(8.7\times {10}^6\text{J}/{\text{m}}^{\text{3}}\right)+\left(8.95\times {10}^6\text{J}/{\text{m}}^{\text{3}}\right)+\left(9.15\times {10}^6\text{J}/{\text{m}}^{\text{3}}\right)\\ +\left(9.20\times {10}^6\text{J}/{\text{m}}^{\text{3}}\right)+\left(9.15\times {10}^6\text{J}/{\text{m}}^{\text{3}}\right)+\left(7.26\times {10}^6\text{J}/{\text{m}}^{\text{3}}\right)\end{array}\right]\\ =\left(0.85+4.27+6.7+7.6+8.3+8.7+8.95+9.15+9.20+9.15+7.26\right)\times {10}^6\text{J}/{\text{m}}^{\text{3}}\\ =80.13\times {10}^6\text{J}/{\text{m}}^{\text{3}}\end{array}$

Conclusion:

Thus, the toughness of 1045 steel specimen is $80.13\times {10}^6\text{J}/{\text{m}}^{\text{3}}$ .

(b)

To determine

The comparison of magnitude of $1020$ steel and $1045$ steel.

Explanation of Solution

Introduction:

The toughness of a specimen is defined as the strain energy per unit volume, required to fracture the specimen. Toughness is obtained when the stress-strain diagram to fracture is integrated. Toughness of a specimen plays a major role for its availability as an engineering material.

Refer Example Problem $6.13$ in the textbook “Material Science and Engineering Properties”.

The toughness of $1020$ steel specimen is $92.2\times {10}^6\text{J}/{\text{m}}^{\text{3}}$ , while the toughness of $1045$ steel specimen found in part (a) is $80.13\times {10}^6\text{J}/{\text{m}}^{\text{3}}$ . So, it can be said that 1020 steel specimen is tougher as compared to 1045 steel specimen.

For $1020$ steel, fracture occurs at strain of around $0.19$ while in case of $1045$ steel it occurs at strain of $0.098$ . So, for higher value of fracture strain, toughness is higher, that is why the toughness of $1020$ steel specimen is more as compare to $1045$ steel specimen.

Conclusion:

Thus, the 1020 steel specimen is tougher as compared to 1045 steel specimen.