Precalculus: Mathematics for Calculus - 6th Edition
6th Edition
ISBN: 9780840068071
Author: Stewart, James, Redlin, Lothar, Watson, Saleem
Publisher: Cengage Learning
expand_more
expand_more
format_list_bulleted
Videos
Textbook Question
Chapter 5.6, Problem 43E
Electric Generator The graph shows an oscilloscope reading of the variation in voltage of an AC current produced by a simple generator.
- (a) Find the maximum voltage produced.
- (b) Find the frequency (cycles per second) of the generator.
- (c) How many revolutions per second does the armature in the generator make?
- (d) Find a formula that describes the variation in voltage as a function of time.
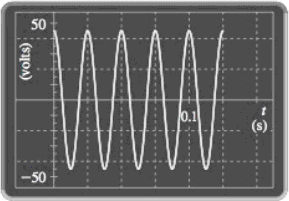
(a)
Expert Solution
To determine
The value of maximum voltage produced by the generator.
Explanation of Solution
The graph which shows the variation of voltage of an AC current produced by a simple generator is given below.
Figure (1)
From the Figure (1), it is noticed that the maximum voltage of the curve lies on the y-axis at 45.
Thus, the value of maximum voltage is
(b)
Expert Solution
To determine
The frequency of the generator.
Explanation of Solution
The graph for the voltage is variation is given below.
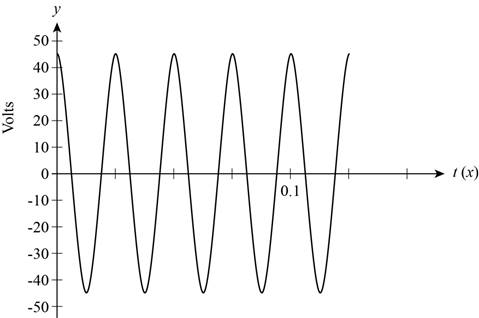
Figure (1)
From the Figure (1) it is noticed that the period of the sine curve is
Thus, the frequency of the sine curve is defined as,
(c)
Expert Solution
To determine
The number of revolution per second the armature takes in the generator.
Explanation of Solution
The one revolution of the armature generates one cycle of voltage.
The frequency of the voltage is
So, the value of one revolution of armature is
(d)
Expert Solution
To determine
The formula that describes the variation in voltage as a time function.
Explanation of Solution
The graph for the voltage is variation is given below,
Figure (1)
From the Figure (1) it is noticed that the period of the sine curve is
Since the waves starts from positive 45 then, the formula of frequency,
Substitute 40 for f in the above formula,
The general equation for simple harmonic motion is,
Substitute
Thus the general formula of voltage variation is
Chapter 5 Solutions
Precalculus: Mathematics for Calculus - 6th Edition
Ch. 5.1 - Prob. 1ECh. 5.1 - Prob. 2ECh. 5.1 - Prob. 3ECh. 5.1 - Prob. 4ECh. 5.1 - Prob. 5ECh. 5.1 - Prob. 6ECh. 5.1 - Prob. 7ECh. 5.1 - Prob. 8ECh. 5.1 - Prob. 9ECh. 5.1 - Prob. 10E
Ch. 5.1 - Prob. 11ECh. 5.1 - Prob. 12ECh. 5.1 - Prob. 13ECh. 5.1 - Prob. 14ECh. 5.1 - Prob. 15ECh. 5.1 - Prob. 16ECh. 5.1 - Prob. 17ECh. 5.1 - Prob. 18ECh. 5.1 - Prob. 19ECh. 5.1 - Prob. 20ECh. 5.1 - Prob. 21ECh. 5.1 - Prob. 22ECh. 5.1 - Prob. 23ECh. 5.1 - Prob. 24ECh. 5.1 - Prob. 25ECh. 5.1 - Prob. 26ECh. 5.1 - Prob. 27ECh. 5.1 - Prob. 28ECh. 5.1 - Prob. 29ECh. 5.1 - Prob. 30ECh. 5.1 - Prob. 31ECh. 5.1 - Prob. 32ECh. 5.1 - Prob. 33ECh. 5.1 - Prob. 34ECh. 5.1 - Prob. 35ECh. 5.1 - Prob. 36ECh. 5.1 - Prob. 37ECh. 5.1 - Prob. 38ECh. 5.1 - Prob. 39ECh. 5.1 - Prob. 40ECh. 5.1 - Prob. 41ECh. 5.1 - Prob. 42ECh. 5.1 - Prob. 43ECh. 5.1 - Prob. 44ECh. 5.1 - Prob. 45ECh. 5.1 - Prob. 46ECh. 5.1 - Prob. 47ECh. 5.1 - Prob. 48ECh. 5.1 - Prob. 49ECh. 5.1 - Prob. 50ECh. 5.1 - Prob. 51ECh. 5.1 - Prob. 52ECh. 5.1 - Prob. 53ECh. 5.1 - Prob. 54ECh. 5.1 - Prob. 55ECh. 5.1 - Prob. 56ECh. 5.1 - Prob. 57ECh. 5.1 - Prob. 58ECh. 5.2 - Let P(x, y) be the terminal point on the unit...Ch. 5.2 - If P(x, y) is on the unit circle, then x2 + y2 =...Ch. 5.2 - Prob. 3ECh. 5.2 - Prob. 4ECh. 5.2 - Prob. 5ECh. 5.2 - Prob. 6ECh. 5.2 - Prob. 7ECh. 5.2 - Prob. 8ECh. 5.2 - Prob. 9ECh. 5.2 - Prob. 10ECh. 5.2 - Prob. 11ECh. 5.2 - Prob. 12ECh. 5.2 - Prob. 13ECh. 5.2 - Prob. 14ECh. 5.2 - Prob. 15ECh. 5.2 - Prob. 16ECh. 5.2 - Prob. 17ECh. 5.2 - Prob. 18ECh. 5.2 - Prob. 19ECh. 5.2 - Prob. 20ECh. 5.2 - Prob. 21ECh. 5.2 - Prob. 22ECh. 5.2 - Prob. 23ECh. 5.2 - Prob. 24ECh. 5.2 - Prob. 25ECh. 5.2 - Prob. 26ECh. 5.2 - Prob. 27ECh. 5.2 - Prob. 28ECh. 5.2 - Prob. 29ECh. 5.2 - Prob. 30ECh. 5.2 - Prob. 31ECh. 5.2 - Prob. 32ECh. 5.2 - Prob. 33ECh. 5.2 - Prob. 34ECh. 5.2 - Prob. 35ECh. 5.2 - Prob. 36ECh. 5.2 - Prob. 37ECh. 5.2 - Prob. 38ECh. 5.2 - Prob. 39ECh. 5.2 - Prob. 40ECh. 5.2 - Prob. 41ECh. 5.2 - Prob. 42ECh. 5.2 - Prob. 43ECh. 5.2 - Prob. 44ECh. 5.2 - Prob. 45ECh. 5.2 - Prob. 46ECh. 5.2 - Prob. 47ECh. 5.2 - Prob. 48ECh. 5.2 - Prob. 49ECh. 5.2 - Prob. 50ECh. 5.2 - Prob. 51ECh. 5.2 - Prob. 52ECh. 5.2 - Prob. 53ECh. 5.2 - Prob. 54ECh. 5.2 - Prob. 55ECh. 5.2 - Prob. 56ECh. 5.2 - Prob. 57ECh. 5.2 - Prob. 58ECh. 5.2 - Prob. 59ECh. 5.2 - Prob. 60ECh. 5.2 - Prob. 61ECh. 5.2 - Prob. 62ECh. 5.2 - Prob. 63ECh. 5.2 - Prob. 64ECh. 5.2 - Prob. 65ECh. 5.2 - Prob. 66ECh. 5.2 - Prob. 67ECh. 5.2 - Prob. 68ECh. 5.2 - Prob. 69ECh. 5.2 - Prob. 70ECh. 5.2 - Prob. 71ECh. 5.2 - Prob. 72ECh. 5.2 - Prob. 73ECh. 5.2 - Prob. 74ECh. 5.2 - Prob. 75ECh. 5.2 - Prob. 76ECh. 5.2 - Prob. 77ECh. 5.2 - Prob. 78ECh. 5.2 - Prob. 79ECh. 5.2 - Prob. 80ECh. 5.2 - Prob. 81ECh. 5.2 - Circadian Rhythms Everybodys blood pressure varies...Ch. 5.2 - Electric Circuit After the switch is closed in the...Ch. 5.2 - Bungee Jumping A bungee jumper plummets from a...Ch. 5.2 - Prob. 85ECh. 5.2 - Prob. 86ECh. 5.3 - Prob. 1ECh. 5.3 - Prob. 2ECh. 5.3 - Prob. 3ECh. 5.3 - Prob. 4ECh. 5.3 - Prob. 5ECh. 5.3 - Prob. 6ECh. 5.3 - Prob. 7ECh. 5.3 - Prob. 8ECh. 5.3 - Prob. 9ECh. 5.3 - Prob. 10ECh. 5.3 - Prob. 11ECh. 5.3 - Prob. 12ECh. 5.3 - Prob. 13ECh. 5.3 - Prob. 14ECh. 5.3 - Prob. 15ECh. 5.3 - Prob. 16ECh. 5.3 - Prob. 17ECh. 5.3 - Prob. 18ECh. 5.3 - Prob. 19ECh. 5.3 - Prob. 20ECh. 5.3 - Prob. 21ECh. 5.3 - Prob. 22ECh. 5.3 - Prob. 23ECh. 5.3 - Prob. 24ECh. 5.3 - Prob. 25ECh. 5.3 - Prob. 26ECh. 5.3 - Prob. 27ECh. 5.3 - Prob. 28ECh. 5.3 - Prob. 29ECh. 5.3 - Prob. 30ECh. 5.3 - Prob. 31ECh. 5.3 - Prob. 32ECh. 5.3 - Prob. 33ECh. 5.3 - Prob. 34ECh. 5.3 - Prob. 35ECh. 5.3 - Prob. 36ECh. 5.3 - Prob. 37ECh. 5.3 - Prob. 38ECh. 5.3 - Prob. 39ECh. 5.3 - Prob. 40ECh. 5.3 - Prob. 41ECh. 5.3 - Prob. 42ECh. 5.3 - Prob. 43ECh. 5.3 - Prob. 44ECh. 5.3 - Prob. 45ECh. 5.3 - Prob. 46ECh. 5.3 - Prob. 47ECh. 5.3 - Prob. 48ECh. 5.3 - Prob. 49ECh. 5.3 - Prob. 50ECh. 5.3 - Prob. 51ECh. 5.3 - Prob. 52ECh. 5.3 - Prob. 53ECh. 5.3 - Prob. 54ECh. 5.3 - Prob. 55ECh. 5.3 - Prob. 56ECh. 5.3 - Prob. 57ECh. 5.3 - Prob. 58ECh. 5.3 - Prob. 59ECh. 5.3 - Prob. 60ECh. 5.3 - Prob. 61ECh. 5.3 - Prob. 62ECh. 5.3 - Prob. 63ECh. 5.3 - Prob. 64ECh. 5.3 - Prob. 65ECh. 5.3 - Prob. 66ECh. 5.3 - Prob. 67ECh. 5.3 - Prob. 68ECh. 5.3 - Prob. 69ECh. 5.3 - Prob. 70ECh. 5.3 - Prob. 71ECh. 5.3 - Prob. 72ECh. 5.3 - Prob. 73ECh. 5.3 - Prob. 74ECh. 5.3 - Prob. 75ECh. 5.3 - Prob. 76ECh. 5.3 - Height of a Wave As a wave passes by an offshore...Ch. 5.3 - Sound Vibrations A tuning fork is struck,...Ch. 5.3 - Blood Pressure Each time your heart beats, your...Ch. 5.3 - Variable Stars Variable stars are ones whose...Ch. 5.3 - Prob. 81ECh. 5.3 - Prob. 82ECh. 5.3 - Prob. 83ECh. 5.3 - Prob. 84ECh. 5.4 - The trigonometric function y = tan x has period...Ch. 5.4 - The trigonometric function y = csc x has period...Ch. 5.4 - Prob. 3ECh. 5.4 - Prob. 4ECh. 5.4 - Prob. 5ECh. 5.4 - Prob. 6ECh. 5.4 - Prob. 7ECh. 5.4 - Prob. 8ECh. 5.4 - Prob. 9ECh. 5.4 - Prob. 10ECh. 5.4 - Prob. 11ECh. 5.4 - Prob. 12ECh. 5.4 - Prob. 13ECh. 5.4 - Prob. 14ECh. 5.4 - Prob. 15ECh. 5.4 - Prob. 16ECh. 5.4 - Prob. 17ECh. 5.4 - Prob. 18ECh. 5.4 - Prob. 19ECh. 5.4 - Prob. 20ECh. 5.4 - Prob. 21ECh. 5.4 - Prob. 22ECh. 5.4 - Prob. 23ECh. 5.4 - Prob. 24ECh. 5.4 - Prob. 25ECh. 5.4 - Prob. 26ECh. 5.4 - Prob. 27ECh. 5.4 - Prob. 28ECh. 5.4 - Prob. 29ECh. 5.4 - Prob. 30ECh. 5.4 - Prob. 31ECh. 5.4 - Prob. 32ECh. 5.4 - Prob. 33ECh. 5.4 - Prob. 34ECh. 5.4 - Prob. 35ECh. 5.4 - Prob. 36ECh. 5.4 - Prob. 37ECh. 5.4 - Prob. 38ECh. 5.4 - Prob. 39ECh. 5.4 - Prob. 40ECh. 5.4 - Prob. 41ECh. 5.4 - Prob. 42ECh. 5.4 - Prob. 43ECh. 5.4 - Prob. 44ECh. 5.4 - Prob. 45ECh. 5.4 - Prob. 46ECh. 5.4 - Prob. 47ECh. 5.4 - Prob. 48ECh. 5.4 - Prob. 49ECh. 5.4 - Prob. 50ECh. 5.4 - Prob. 51ECh. 5.4 - Prob. 52ECh. 5.4 - Prob. 53ECh. 5.4 - Prob. 54ECh. 5.4 - Prob. 55ECh. 5.4 - Prob. 56ECh. 5.4 - Lighthouse The beam from a lighthouse completes...Ch. 5.4 - Length of a Shadow On a day when the sun passes...Ch. 5.4 - Prob. 59ECh. 5.5 - (a) To define the inverse sine function, we...Ch. 5.5 - The cancellation property sin1(sin x) = x is valid...Ch. 5.5 - Prob. 3ECh. 5.5 - Prob. 4ECh. 5.5 - Prob. 5ECh. 5.5 - Prob. 6ECh. 5.5 - Prob. 7ECh. 5.5 - Prob. 8ECh. 5.5 - Prob. 9ECh. 5.5 - Prob. 10ECh. 5.5 - Prob. 11ECh. 5.5 - Prob. 12ECh. 5.5 - Prob. 13ECh. 5.5 - Prob. 14ECh. 5.5 - Prob. 15ECh. 5.5 - Prob. 16ECh. 5.5 - Prob. 17ECh. 5.5 - Prob. 18ECh. 5.5 - Prob. 19ECh. 5.5 - Prob. 20ECh. 5.5 - Prob. 21ECh. 5.5 - Prob. 22ECh. 5.5 - Prob. 23ECh. 5.5 - Prob. 24ECh. 5.5 - Prob. 25ECh. 5.5 - Prob. 26ECh. 5.5 - Prob. 27ECh. 5.5 - Prob. 28ECh. 5.5 - Prob. 29ECh. 5.5 - Prob. 30ECh. 5.5 - Prob. 31ECh. 5.5 - Prob. 32ECh. 5.5 - Prob. 33ECh. 5.5 - Prob. 34ECh. 5.5 - Prob. 35ECh. 5.5 - Prob. 36ECh. 5.5 - Prob. 37ECh. 5.5 - Prob. 38ECh. 5.5 - Prob. 39ECh. 5.5 - Prob. 40ECh. 5.5 - Prob. 41ECh. 5.5 - Prob. 42ECh. 5.5 - Prob. 43ECh. 5.5 - Prob. 44ECh. 5.5 - Prob. 45ECh. 5.5 - Prob. 46ECh. 5.5 - Prob. 47ECh. 5.6 - For an object in simple harmonic motion with...Ch. 5.6 - For an object in damped harmonic motion with...Ch. 5.6 - Prob. 3ECh. 5.6 - Prob. 4ECh. 5.6 - Prob. 5ECh. 5.6 - Prob. 6ECh. 5.6 - Prob. 7ECh. 5.6 - Prob. 8ECh. 5.6 - Prob. 9ECh. 5.6 - Prob. 10ECh. 5.6 - Prob. 11ECh. 5.6 - Prob. 12ECh. 5.6 - Prob. 13ECh. 5.6 - Prob. 14ECh. 5.6 - Prob. 15ECh. 5.6 - Prob. 16ECh. 5.6 - Prob. 17ECh. 5.6 - Prob. 18ECh. 5.6 - Prob. 19ECh. 5.6 - Prob. 20ECh. 5.6 - Prob. 21ECh. 5.6 - Prob. 22ECh. 5.6 - Prob. 23ECh. 5.6 - Prob. 24ECh. 5.6 - Prob. 25ECh. 5.6 - Prob. 26ECh. 5.6 - A Bobbing Cork A cork floating in a lake is...Ch. 5.6 - FM Radio Signals The carrier wave for an FM radio...Ch. 5.6 - Blood Pressure Each time your heart beats, your...Ch. 5.6 - Predator Population Model In a predator/prey...Ch. 5.6 - Prob. 31ECh. 5.6 - Tides The graph shows the variation of the water...Ch. 5.6 - Tides The Bay of Fundy in Nova Scotia has the...Ch. 5.6 - Prob. 34ECh. 5.6 - Prob. 35ECh. 5.6 - Prob. 36ECh. 5.6 - Ferris Wheel A Ferris wheel has a radius of 10 m,...Ch. 5.6 - Cock Pendulum The pendulum in a grandfather clock...Ch. 5.6 - Variable Stars The variable star Zeta Gemini has a...Ch. 5.6 - Variable Stars Astronomers believe that the radius...Ch. 5.6 - Biological Clocks Circadian rhythms are biological...Ch. 5.6 - Electric Generator The armature in an electric...Ch. 5.6 - Electric Generator The graph shows an oscilloscope...Ch. 5.6 - Doppler Effect When a car with its horn blowing...Ch. 5.6 - Motion of a Building A strong gust of wind strikes...Ch. 5.6 - Shock Absorber When a car hits a certain bump on...Ch. 5.6 - Tuning Fork A tuning fork is struck and oscillates...Ch. 5.6 - Guitar String A guitar string is pulled at point P...Ch. 5 - Prob. 1RCCCh. 5 - Prob. 2RCCCh. 5 - Prob. 3RCCCh. 5 - Prob. 4RCCCh. 5 - Prob. 5RCCCh. 5 - Prob. 6RCCCh. 5 - Prob. 7RCCCh. 5 - Prob. 8RCCCh. 5 - Prob. 9RCCCh. 5 - Prob. 10RCCCh. 5 - Prob. 11RCCCh. 5 - Prob. 12RCCCh. 5 - Prob. 1RECh. 5 - Prob. 2RECh. 5 - Prob. 3RECh. 5 - Prob. 4RECh. 5 - Prob. 5RECh. 5 - Prob. 6RECh. 5 - Prob. 7RECh. 5 - Prob. 8RECh. 5 - Prob. 9RECh. 5 - Prob. 10RECh. 5 - Prob. 11RECh. 5 - Prob. 12RECh. 5 - Prob. 13RECh. 5 - Prob. 14RECh. 5 - Prob. 15RECh. 5 - Prob. 16RECh. 5 - Prob. 17RECh. 5 - Prob. 18RECh. 5 - Prob. 19RECh. 5 - Prob. 20RECh. 5 - Prob. 21RECh. 5 - Prob. 22RECh. 5 - Prob. 23RECh. 5 - Prob. 24RECh. 5 - Prob. 25RECh. 5 - Prob. 26RECh. 5 - Prob. 27RECh. 5 - Prob. 28RECh. 5 - Prob. 29RECh. 5 - Prob. 30RECh. 5 - Prob. 31RECh. 5 - Prob. 32RECh. 5 - Prob. 33RECh. 5 - Prob. 34RECh. 5 - Prob. 35RECh. 5 - Prob. 36RECh. 5 - Prob. 37RECh. 5 - Prob. 38RECh. 5 - Prob. 39RECh. 5 - Prob. 40RECh. 5 - Prob. 41RECh. 5 - Prob. 42RECh. 5 - Prob. 43RECh. 5 - Prob. 44RECh. 5 - Prob. 45RECh. 5 - Prob. 46RECh. 5 - Prob. 47RECh. 5 - Prob. 48RECh. 5 - Prob. 49RECh. 5 - Prob. 50RECh. 5 - Prob. 51RECh. 5 - Prob. 52RECh. 5 - Prob. 53RECh. 5 - Prob. 54RECh. 5 - Prob. 55RECh. 5 - Prob. 56RECh. 5 - Prob. 57RECh. 5 - Prob. 58RECh. 5 - Prob. 59RECh. 5 - Prob. 60RECh. 5 - Prob. 61RECh. 5 - Prob. 62RECh. 5 - Prob. 63RECh. 5 - Prob. 64RECh. 5 - Prob. 65RECh. 5 - Prob. 66RECh. 5 - Prob. 67RECh. 5 - Prob. 68RECh. 5 - Prob. 69RECh. 5 - Prob. 70RECh. 5 - Prob. 71RECh. 5 - Prob. 72RECh. 5 - Prob. 1TCh. 5 - The point P in the figure at the left has...Ch. 5 - Prob. 3TCh. 5 - Express tan t in terms of sin t, if the terminal...Ch. 5 - If cost=817 and if the terminal point determined...Ch. 5 - Prob. 6TCh. 5 - Prob. 7TCh. 5 - Prob. 8TCh. 5 - Prob. 9TCh. 5 - Prob. 10TCh. 5 - The graph shown at left is one period of a...Ch. 5 - Prob. 12TCh. 5 - A mass suspended from a spring oscillates in...Ch. 5 - An object is moving up and down in damped harmonic...Ch. 5 - Prob. 1PCh. 5 - Prob. 2PCh. 5 - Prob. 3PCh. 5 - Prob. 4PCh. 5 - Prob. 5PCh. 5 - Prob. 6PCh. 5 - Prob. 7PCh. 5 - Prob. 8PCh. 5 - Prob. 9P
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, calculus and related others by exploring similar questions and additional content below.Similar questions
- 4. Use method of separation of variable to solve the following wave equation მłu J²u subject to u(0,t) =0, for t> 0, u(л,t) = 0, for t> 0, = t> 0, at² ax²' u(x, 0) = 0, 0.01 x, ut(x, 0) = Π 0.01 (π-x), 0arrow_forwardSolve the following heat equation by method of separation variables: ди = at subject to u(0,t) =0, for -16024 ძx2 • t>0, 0 0, ux (4,t) = 0, for t> 0, u(x, 0) = (x-3, \-1, 0 < x ≤2 2≤ x ≤ 4.arrow_forwardex 5. important aspects. Graph f(x)=lnx. Be sure to make your graph big enough to easily read (use the space given.) Label all 6 33arrow_forwardDecide whether each limit exists. If a limit exists, estimate its value. 11. (a) lim f(x) x-3 f(x) ↑ 4 3- 2+ (b) lim f(x) x―0 -2 0 X 1234arrow_forwardDetermine whether the lines L₁ (t) = (-2,3, −1)t + (0,2,-3) and L2 p(s) = (2, −3, 1)s + (-10, 17, -8) intersect. If they do, find the point of intersection.arrow_forwardConvert the line given by the parametric equations y(t) Enter the symmetric equations in alphabetic order. (x(t) = -4+6t = 3-t (z(t) = 5-7t to symmetric equations.arrow_forwardFind the point at which the line (t) = (4, -5,-4)+t(-2, -1,5) intersects the xy plane.arrow_forwardFind the distance from the point (-9, -3, 0) to the line ä(t) = (−4, 1, −1)t + (0, 1, −3) .arrow_forward1 Find a vector parallel to the line defined by the parametric equations (x(t) = -2t y(t) == 1- 9t z(t) = -1-t Additionally, find a point on the line.arrow_forwardFind the (perpendicular) distance from the line given by the parametric equations (x(t) = 5+9t y(t) = 7t = 2-9t z(t) to the point (-1, 1, −3).arrow_forwardLet ä(t) = (3,-2,-5)t + (7,−1, 2) and (u) = (5,0, 3)u + (−3,−9,3). Find the acute angle (in degrees) between the lines:arrow_forwardA tank initially contains 50 gal of pure water. Brine containing 3 lb of salt per gallon enters the tank at 2 gal/min, and the (perfectly mixed) solution leaves the tank at 3 gal/min. Thus, the tank is empty after exactly 50 min. (a) Find the amount of salt in the tank after t minutes. (b) What is the maximum amount of salt ever in the tank?arrow_forwardarrow_back_iosSEE MORE QUESTIONSarrow_forward_ios
Recommended textbooks for you
Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning
Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON
Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning
Calculus: Early Transcendentals
Calculus
ISBN:9781285741550
Author:James Stewart
Publisher:Cengage Learning
Thomas' Calculus (14th Edition)
Calculus
ISBN:9780134438986
Author:Joel R. Hass, Christopher E. Heil, Maurice D. Weir
Publisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)
Calculus
ISBN:9780134763644
Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric Schulz
Publisher:PEARSON
Calculus: Early Transcendentals
Calculus
ISBN:9781319050740
Author:Jon Rogawski, Colin Adams, Robert Franzosa
Publisher:W. H. Freeman
Calculus: Early Transcendental Functions
Calculus
ISBN:9781337552516
Author:Ron Larson, Bruce H. Edwards
Publisher:Cengage Learning
Trigonometry - Harmonic Motion - Equation Setup; Author: David Hays;https://www.youtube.com/watch?v=BPrZnn3DJ6Q;License: Standard YouTube License, CC-BY
Simple Harmonic Motion - An introduction : ExamSolutions Maths Revision; Author: ExamSolutions;https://www.youtube.com/watch?v=tH2vldyP5OE;License: Standard YouTube License, CC-BY