Precalculus: Mathematics for Calculus - 6th Edition
6th Edition
ISBN: 9780840068071
Author: Stewart, James, Redlin, Lothar, Watson, Saleem
Publisher: Cengage Learning
expand_more
expand_more
format_list_bulleted
Videos
Question
Chapter 5, Problem 9P
a.
To determine
Sketch a
a.
Expert Solution
Answer to Problem 9P
The scatter plot is
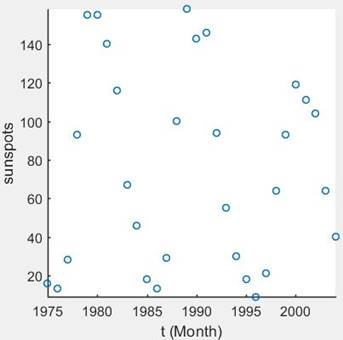
Explanation of Solution
Given: A set of the data is,
Calculation:
Let’s take a given data set sketch a scatter plot using MATLAB.
The function is using in the MATLAB to sketch a scatter plot is,
Program:
clc
clear
close all
t=1975:1:2004;
y=[16 13 28 93 155 155 140 116 67 46 18 13 29 100 158 ...
143 146 94 55 30 18 9 21 64 93 119 111 104 64 40];
scatter(t,y,'linewidth',1.25');
set(gca,'Linewidth',1.2,'Fontsize',12);
xlabel('t (Month)');
ylabel('sunspots')
axis square
axis tight
Query:
- First, we have defined the given data sets.
- Then using a function “scatter (t, y)” sketch a scatter plot.
b.
To determine
Calculate the cosine function using given data set.
b.
Expert Solution
Answer to Problem 9P
The cosine function is,
Explanation of Solution
Given: A set of the data is,
Calculation:
First, we have to write a general equation of the cosine function,
Then, calculate the vertical shifting as,
Calculate the amplitude as,
Then, Calculate the phase shift as,
The value of c is,
Put all the value into the equation (1) then,
Program:
clc
clear
close all
t=1975:1:2004;
y=[16 13 28 93 155 155 140 116 67 46 18 13 29 100 158 ...
143 146 94 55 30 18 9 21 64 93 119 111 104 64 40];
b=(1/2)*(max(y)+min(y));
a=(1/2)*(max(y)-min(y));
w=2*pi/30;
idx=find(y==max(y));
c=t(idx);
f=(a*cos(w*(t-c)))+b;
Query:
- First, we have defined the given data sets.
- Then calculate the value of b, a, w, and c.
- Put all the values into the equation of cosine function and get the solution.
c.
To determine
Sketch a graph of the function which is found in part (b).
c.
Expert Solution
Answer to Problem 9P
The solution is,
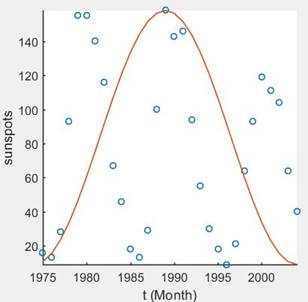
Explanation of Solution
Given: A set of the data is,
Calculation:
Sketch a graph of the cosine function in MATLAB using function “plot (f, t)”.
The function is found in part (b) is,
Program:
clc
clear
close all
t=1975:1:2004;
y=[16 13 28 93 155 155 140 116 67 46 18 13 29 100 158 ...
143 146 94 55 30 18 9 21 64 93 119 111 104 64 40];
b=(1/2)*(max(y)+min(y));
a=(1/2)*(max(y)-min(y));
w=2*pi/30;
idx=find(y==max(y));
c=t(idx);
f=(a*cos(w*(t-c)))+b;
scatter(t,y,'linewidth',1.25');
hold on
plot(t,f,'linewidth',1.25');
set(gca,'Linewidth',1.2,'Fontsize',12);
xlabel('t (Month)');
ylabel('sunspots')
axis square
axis tight
Query:
- First, we have defined the given data sets.
- Then calculate the value of b, a, w, and c.
- Put all the values into the equation of cosine function and get the solution.
- Then sketch a graph.
d.
To determine
Calculate the sine function using given data set.
d.
Expert Solution
Answer to Problem 9P
The cosine function is,
And the best fitting curve is,
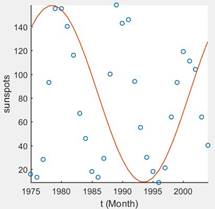
Explanation of Solution
Given: A set of the data is,
Calculation:
First, we have to write a general equation of the cosine function,
Then, calculate the vertical shifting as,
Calculate the amplitude as,
Then, Calculate the phase shift as,
The value of c is,
Put all the value into the equation (1) then,
Program:
clc
clear
close all
t=1975:1:2004;
y=[16 13 28 93 155 155 140 116 67 46 18 13 29 100 158 ...
143 146 94 55 30 18 9 21 64 93 119 111 104 64 40];
b=(1/2)*(max(y)+min(y));
a=(1/2)*(max(y)-min(y));
w=2*pi/30;
idx=find(y==max(y));
c=t(idx);
f=(a*sin(w*(t+c)))+b;
scatter(t,y,'linewidth',1.25');
hold on
plot(t,f,'linewidth',1.25');
set(gca,'Linewidth',1.2,'Fontsize',12);
xlabel('t (Month)');
ylabel('sunspots')
axis square
axis tight
Query:
- First, we have defined the given data sets.
- Then calculate the value of b, a, w, and c.
- Put all the values into the equation of cosine function and get the solution.
- Then sketch a best fitting curve with the scatter plot.
Chapter 5 Solutions
Precalculus: Mathematics for Calculus - 6th Edition
Ch. 5.1 - Prob. 1ECh. 5.1 - Prob. 2ECh. 5.1 - Prob. 3ECh. 5.1 - Prob. 4ECh. 5.1 - Prob. 5ECh. 5.1 - Prob. 6ECh. 5.1 - Prob. 7ECh. 5.1 - Prob. 8ECh. 5.1 - Prob. 9ECh. 5.1 - Prob. 10E
Ch. 5.1 - Prob. 11ECh. 5.1 - Prob. 12ECh. 5.1 - Prob. 13ECh. 5.1 - Prob. 14ECh. 5.1 - Prob. 15ECh. 5.1 - Prob. 16ECh. 5.1 - Prob. 17ECh. 5.1 - Prob. 18ECh. 5.1 - Prob. 19ECh. 5.1 - Prob. 20ECh. 5.1 - Prob. 21ECh. 5.1 - Prob. 22ECh. 5.1 - Prob. 23ECh. 5.1 - Prob. 24ECh. 5.1 - Prob. 25ECh. 5.1 - Prob. 26ECh. 5.1 - Prob. 27ECh. 5.1 - Prob. 28ECh. 5.1 - Prob. 29ECh. 5.1 - Prob. 30ECh. 5.1 - Prob. 31ECh. 5.1 - Prob. 32ECh. 5.1 - Prob. 33ECh. 5.1 - Prob. 34ECh. 5.1 - Prob. 35ECh. 5.1 - Prob. 36ECh. 5.1 - Prob. 37ECh. 5.1 - Prob. 38ECh. 5.1 - Prob. 39ECh. 5.1 - Prob. 40ECh. 5.1 - Prob. 41ECh. 5.1 - Prob. 42ECh. 5.1 - Prob. 43ECh. 5.1 - Prob. 44ECh. 5.1 - Prob. 45ECh. 5.1 - Prob. 46ECh. 5.1 - Prob. 47ECh. 5.1 - Prob. 48ECh. 5.1 - Prob. 49ECh. 5.1 - Prob. 50ECh. 5.1 - Prob. 51ECh. 5.1 - Prob. 52ECh. 5.1 - Prob. 53ECh. 5.1 - Prob. 54ECh. 5.1 - Prob. 55ECh. 5.1 - Prob. 56ECh. 5.1 - Prob. 57ECh. 5.1 - Prob. 58ECh. 5.2 - Let P(x, y) be the terminal point on the unit...Ch. 5.2 - If P(x, y) is on the unit circle, then x2 + y2 =...Ch. 5.2 - Prob. 3ECh. 5.2 - Prob. 4ECh. 5.2 - Prob. 5ECh. 5.2 - Prob. 6ECh. 5.2 - Prob. 7ECh. 5.2 - Prob. 8ECh. 5.2 - Prob. 9ECh. 5.2 - Prob. 10ECh. 5.2 - Prob. 11ECh. 5.2 - Prob. 12ECh. 5.2 - Prob. 13ECh. 5.2 - Prob. 14ECh. 5.2 - Prob. 15ECh. 5.2 - Prob. 16ECh. 5.2 - Prob. 17ECh. 5.2 - Prob. 18ECh. 5.2 - Prob. 19ECh. 5.2 - Prob. 20ECh. 5.2 - Prob. 21ECh. 5.2 - Prob. 22ECh. 5.2 - Prob. 23ECh. 5.2 - Prob. 24ECh. 5.2 - Prob. 25ECh. 5.2 - Prob. 26ECh. 5.2 - Prob. 27ECh. 5.2 - Prob. 28ECh. 5.2 - Prob. 29ECh. 5.2 - Prob. 30ECh. 5.2 - Prob. 31ECh. 5.2 - Prob. 32ECh. 5.2 - Prob. 33ECh. 5.2 - Prob. 34ECh. 5.2 - Prob. 35ECh. 5.2 - Prob. 36ECh. 5.2 - Prob. 37ECh. 5.2 - Prob. 38ECh. 5.2 - Prob. 39ECh. 5.2 - Prob. 40ECh. 5.2 - Prob. 41ECh. 5.2 - Prob. 42ECh. 5.2 - Prob. 43ECh. 5.2 - Prob. 44ECh. 5.2 - Prob. 45ECh. 5.2 - Prob. 46ECh. 5.2 - Prob. 47ECh. 5.2 - Prob. 48ECh. 5.2 - Prob. 49ECh. 5.2 - Prob. 50ECh. 5.2 - Prob. 51ECh. 5.2 - Prob. 52ECh. 5.2 - Prob. 53ECh. 5.2 - Prob. 54ECh. 5.2 - Prob. 55ECh. 5.2 - Prob. 56ECh. 5.2 - Prob. 57ECh. 5.2 - Prob. 58ECh. 5.2 - Prob. 59ECh. 5.2 - Prob. 60ECh. 5.2 - Prob. 61ECh. 5.2 - Prob. 62ECh. 5.2 - Prob. 63ECh. 5.2 - Prob. 64ECh. 5.2 - Prob. 65ECh. 5.2 - Prob. 66ECh. 5.2 - Prob. 67ECh. 5.2 - Prob. 68ECh. 5.2 - Prob. 69ECh. 5.2 - Prob. 70ECh. 5.2 - Prob. 71ECh. 5.2 - Prob. 72ECh. 5.2 - Prob. 73ECh. 5.2 - Prob. 74ECh. 5.2 - Prob. 75ECh. 5.2 - Prob. 76ECh. 5.2 - Prob. 77ECh. 5.2 - Prob. 78ECh. 5.2 - Prob. 79ECh. 5.2 - Prob. 80ECh. 5.2 - Prob. 81ECh. 5.2 - Circadian Rhythms Everybodys blood pressure varies...Ch. 5.2 - Electric Circuit After the switch is closed in the...Ch. 5.2 - Bungee Jumping A bungee jumper plummets from a...Ch. 5.2 - Prob. 85ECh. 5.2 - Prob. 86ECh. 5.3 - Prob. 1ECh. 5.3 - Prob. 2ECh. 5.3 - Prob. 3ECh. 5.3 - Prob. 4ECh. 5.3 - Prob. 5ECh. 5.3 - Prob. 6ECh. 5.3 - Prob. 7ECh. 5.3 - Prob. 8ECh. 5.3 - Prob. 9ECh. 5.3 - Prob. 10ECh. 5.3 - Prob. 11ECh. 5.3 - Prob. 12ECh. 5.3 - Prob. 13ECh. 5.3 - Prob. 14ECh. 5.3 - Prob. 15ECh. 5.3 - Prob. 16ECh. 5.3 - Prob. 17ECh. 5.3 - Prob. 18ECh. 5.3 - Prob. 19ECh. 5.3 - Prob. 20ECh. 5.3 - Prob. 21ECh. 5.3 - Prob. 22ECh. 5.3 - Prob. 23ECh. 5.3 - Prob. 24ECh. 5.3 - Prob. 25ECh. 5.3 - Prob. 26ECh. 5.3 - Prob. 27ECh. 5.3 - Prob. 28ECh. 5.3 - Prob. 29ECh. 5.3 - Prob. 30ECh. 5.3 - Prob. 31ECh. 5.3 - Prob. 32ECh. 5.3 - Prob. 33ECh. 5.3 - Prob. 34ECh. 5.3 - Prob. 35ECh. 5.3 - Prob. 36ECh. 5.3 - Prob. 37ECh. 5.3 - Prob. 38ECh. 5.3 - Prob. 39ECh. 5.3 - Prob. 40ECh. 5.3 - Prob. 41ECh. 5.3 - Prob. 42ECh. 5.3 - Prob. 43ECh. 5.3 - Prob. 44ECh. 5.3 - Prob. 45ECh. 5.3 - Prob. 46ECh. 5.3 - Prob. 47ECh. 5.3 - Prob. 48ECh. 5.3 - Prob. 49ECh. 5.3 - Prob. 50ECh. 5.3 - Prob. 51ECh. 5.3 - Prob. 52ECh. 5.3 - Prob. 53ECh. 5.3 - Prob. 54ECh. 5.3 - Prob. 55ECh. 5.3 - Prob. 56ECh. 5.3 - Prob. 57ECh. 5.3 - Prob. 58ECh. 5.3 - Prob. 59ECh. 5.3 - Prob. 60ECh. 5.3 - Prob. 61ECh. 5.3 - Prob. 62ECh. 5.3 - Prob. 63ECh. 5.3 - Prob. 64ECh. 5.3 - Prob. 65ECh. 5.3 - Prob. 66ECh. 5.3 - Prob. 67ECh. 5.3 - Prob. 68ECh. 5.3 - Prob. 69ECh. 5.3 - Prob. 70ECh. 5.3 - Prob. 71ECh. 5.3 - Prob. 72ECh. 5.3 - Prob. 73ECh. 5.3 - Prob. 74ECh. 5.3 - Prob. 75ECh. 5.3 - Prob. 76ECh. 5.3 - Height of a Wave As a wave passes by an offshore...Ch. 5.3 - Sound Vibrations A tuning fork is struck,...Ch. 5.3 - Blood Pressure Each time your heart beats, your...Ch. 5.3 - Variable Stars Variable stars are ones whose...Ch. 5.3 - Prob. 81ECh. 5.3 - Prob. 82ECh. 5.3 - Prob. 83ECh. 5.3 - Prob. 84ECh. 5.4 - The trigonometric function y = tan x has period...Ch. 5.4 - The trigonometric function y = csc x has period...Ch. 5.4 - Prob. 3ECh. 5.4 - Prob. 4ECh. 5.4 - Prob. 5ECh. 5.4 - Prob. 6ECh. 5.4 - Prob. 7ECh. 5.4 - Prob. 8ECh. 5.4 - Prob. 9ECh. 5.4 - Prob. 10ECh. 5.4 - Prob. 11ECh. 5.4 - Prob. 12ECh. 5.4 - Prob. 13ECh. 5.4 - Prob. 14ECh. 5.4 - Prob. 15ECh. 5.4 - Prob. 16ECh. 5.4 - Prob. 17ECh. 5.4 - Prob. 18ECh. 5.4 - Prob. 19ECh. 5.4 - Prob. 20ECh. 5.4 - Prob. 21ECh. 5.4 - Prob. 22ECh. 5.4 - Prob. 23ECh. 5.4 - Prob. 24ECh. 5.4 - Prob. 25ECh. 5.4 - Prob. 26ECh. 5.4 - Prob. 27ECh. 5.4 - Prob. 28ECh. 5.4 - Prob. 29ECh. 5.4 - Prob. 30ECh. 5.4 - Prob. 31ECh. 5.4 - Prob. 32ECh. 5.4 - Prob. 33ECh. 5.4 - Prob. 34ECh. 5.4 - Prob. 35ECh. 5.4 - Prob. 36ECh. 5.4 - Prob. 37ECh. 5.4 - Prob. 38ECh. 5.4 - Prob. 39ECh. 5.4 - Prob. 40ECh. 5.4 - Prob. 41ECh. 5.4 - Prob. 42ECh. 5.4 - Prob. 43ECh. 5.4 - Prob. 44ECh. 5.4 - Prob. 45ECh. 5.4 - Prob. 46ECh. 5.4 - Prob. 47ECh. 5.4 - Prob. 48ECh. 5.4 - Prob. 49ECh. 5.4 - Prob. 50ECh. 5.4 - Prob. 51ECh. 5.4 - Prob. 52ECh. 5.4 - Prob. 53ECh. 5.4 - Prob. 54ECh. 5.4 - Prob. 55ECh. 5.4 - Prob. 56ECh. 5.4 - Lighthouse The beam from a lighthouse completes...Ch. 5.4 - Length of a Shadow On a day when the sun passes...Ch. 5.4 - Prob. 59ECh. 5.5 - (a) To define the inverse sine function, we...Ch. 5.5 - The cancellation property sin1(sin x) = x is valid...Ch. 5.5 - Prob. 3ECh. 5.5 - Prob. 4ECh. 5.5 - Prob. 5ECh. 5.5 - Prob. 6ECh. 5.5 - Prob. 7ECh. 5.5 - Prob. 8ECh. 5.5 - Prob. 9ECh. 5.5 - Prob. 10ECh. 5.5 - Prob. 11ECh. 5.5 - Prob. 12ECh. 5.5 - Prob. 13ECh. 5.5 - Prob. 14ECh. 5.5 - Prob. 15ECh. 5.5 - Prob. 16ECh. 5.5 - Prob. 17ECh. 5.5 - Prob. 18ECh. 5.5 - Prob. 19ECh. 5.5 - Prob. 20ECh. 5.5 - Prob. 21ECh. 5.5 - Prob. 22ECh. 5.5 - Prob. 23ECh. 5.5 - Prob. 24ECh. 5.5 - Prob. 25ECh. 5.5 - Prob. 26ECh. 5.5 - Prob. 27ECh. 5.5 - Prob. 28ECh. 5.5 - Prob. 29ECh. 5.5 - Prob. 30ECh. 5.5 - Prob. 31ECh. 5.5 - Prob. 32ECh. 5.5 - Prob. 33ECh. 5.5 - Prob. 34ECh. 5.5 - Prob. 35ECh. 5.5 - Prob. 36ECh. 5.5 - Prob. 37ECh. 5.5 - Prob. 38ECh. 5.5 - Prob. 39ECh. 5.5 - Prob. 40ECh. 5.5 - Prob. 41ECh. 5.5 - Prob. 42ECh. 5.5 - Prob. 43ECh. 5.5 - Prob. 44ECh. 5.5 - Prob. 45ECh. 5.5 - Prob. 46ECh. 5.5 - Prob. 47ECh. 5.6 - For an object in simple harmonic motion with...Ch. 5.6 - For an object in damped harmonic motion with...Ch. 5.6 - Prob. 3ECh. 5.6 - Prob. 4ECh. 5.6 - Prob. 5ECh. 5.6 - Prob. 6ECh. 5.6 - Prob. 7ECh. 5.6 - Prob. 8ECh. 5.6 - Prob. 9ECh. 5.6 - Prob. 10ECh. 5.6 - Prob. 11ECh. 5.6 - Prob. 12ECh. 5.6 - Prob. 13ECh. 5.6 - Prob. 14ECh. 5.6 - Prob. 15ECh. 5.6 - Prob. 16ECh. 5.6 - Prob. 17ECh. 5.6 - Prob. 18ECh. 5.6 - Prob. 19ECh. 5.6 - Prob. 20ECh. 5.6 - Prob. 21ECh. 5.6 - Prob. 22ECh. 5.6 - Prob. 23ECh. 5.6 - Prob. 24ECh. 5.6 - Prob. 25ECh. 5.6 - Prob. 26ECh. 5.6 - A Bobbing Cork A cork floating in a lake is...Ch. 5.6 - FM Radio Signals The carrier wave for an FM radio...Ch. 5.6 - Blood Pressure Each time your heart beats, your...Ch. 5.6 - Predator Population Model In a predator/prey...Ch. 5.6 - Prob. 31ECh. 5.6 - Tides The graph shows the variation of the water...Ch. 5.6 - Tides The Bay of Fundy in Nova Scotia has the...Ch. 5.6 - Prob. 34ECh. 5.6 - Prob. 35ECh. 5.6 - Prob. 36ECh. 5.6 - Ferris Wheel A Ferris wheel has a radius of 10 m,...Ch. 5.6 - Cock Pendulum The pendulum in a grandfather clock...Ch. 5.6 - Variable Stars The variable star Zeta Gemini has a...Ch. 5.6 - Variable Stars Astronomers believe that the radius...Ch. 5.6 - Biological Clocks Circadian rhythms are biological...Ch. 5.6 - Electric Generator The armature in an electric...Ch. 5.6 - Electric Generator The graph shows an oscilloscope...Ch. 5.6 - Doppler Effect When a car with its horn blowing...Ch. 5.6 - Motion of a Building A strong gust of wind strikes...Ch. 5.6 - Shock Absorber When a car hits a certain bump on...Ch. 5.6 - Tuning Fork A tuning fork is struck and oscillates...Ch. 5.6 - Guitar String A guitar string is pulled at point P...Ch. 5 - Prob. 1RCCCh. 5 - Prob. 2RCCCh. 5 - Prob. 3RCCCh. 5 - Prob. 4RCCCh. 5 - Prob. 5RCCCh. 5 - Prob. 6RCCCh. 5 - Prob. 7RCCCh. 5 - Prob. 8RCCCh. 5 - Prob. 9RCCCh. 5 - Prob. 10RCCCh. 5 - Prob. 11RCCCh. 5 - Prob. 12RCCCh. 5 - Prob. 1RECh. 5 - Prob. 2RECh. 5 - Prob. 3RECh. 5 - Prob. 4RECh. 5 - Prob. 5RECh. 5 - Prob. 6RECh. 5 - Prob. 7RECh. 5 - Prob. 8RECh. 5 - Prob. 9RECh. 5 - Prob. 10RECh. 5 - Prob. 11RECh. 5 - Prob. 12RECh. 5 - Prob. 13RECh. 5 - Prob. 14RECh. 5 - Prob. 15RECh. 5 - Prob. 16RECh. 5 - Prob. 17RECh. 5 - Prob. 18RECh. 5 - Prob. 19RECh. 5 - Prob. 20RECh. 5 - Prob. 21RECh. 5 - Prob. 22RECh. 5 - Prob. 23RECh. 5 - Prob. 24RECh. 5 - Prob. 25RECh. 5 - Prob. 26RECh. 5 - Prob. 27RECh. 5 - Prob. 28RECh. 5 - Prob. 29RECh. 5 - Prob. 30RECh. 5 - Prob. 31RECh. 5 - Prob. 32RECh. 5 - Prob. 33RECh. 5 - Prob. 34RECh. 5 - Prob. 35RECh. 5 - Prob. 36RECh. 5 - Prob. 37RECh. 5 - Prob. 38RECh. 5 - Prob. 39RECh. 5 - Prob. 40RECh. 5 - Prob. 41RECh. 5 - Prob. 42RECh. 5 - Prob. 43RECh. 5 - Prob. 44RECh. 5 - Prob. 45RECh. 5 - Prob. 46RECh. 5 - Prob. 47RECh. 5 - Prob. 48RECh. 5 - Prob. 49RECh. 5 - Prob. 50RECh. 5 - Prob. 51RECh. 5 - Prob. 52RECh. 5 - Prob. 53RECh. 5 - Prob. 54RECh. 5 - Prob. 55RECh. 5 - Prob. 56RECh. 5 - Prob. 57RECh. 5 - Prob. 58RECh. 5 - Prob. 59RECh. 5 - Prob. 60RECh. 5 - Prob. 61RECh. 5 - Prob. 62RECh. 5 - Prob. 63RECh. 5 - Prob. 64RECh. 5 - Prob. 65RECh. 5 - Prob. 66RECh. 5 - Prob. 67RECh. 5 - Prob. 68RECh. 5 - Prob. 69RECh. 5 - Prob. 70RECh. 5 - Prob. 71RECh. 5 - Prob. 72RECh. 5 - Prob. 1TCh. 5 - The point P in the figure at the left has...Ch. 5 - Prob. 3TCh. 5 - Express tan t in terms of sin t, if the terminal...Ch. 5 - If cost=817 and if the terminal point determined...Ch. 5 - Prob. 6TCh. 5 - Prob. 7TCh. 5 - Prob. 8TCh. 5 - Prob. 9TCh. 5 - Prob. 10TCh. 5 - The graph shown at left is one period of a...Ch. 5 - Prob. 12TCh. 5 - A mass suspended from a spring oscillates in...Ch. 5 - An object is moving up and down in damped harmonic...Ch. 5 - Prob. 1PCh. 5 - Prob. 2PCh. 5 - Prob. 3PCh. 5 - Prob. 4PCh. 5 - Prob. 5PCh. 5 - Prob. 6PCh. 5 - Prob. 7PCh. 5 - Prob. 8PCh. 5 - Prob. 9P
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, calculus and related others by exploring similar questions and additional content below.Similar questions
- 6. Solve the system of differential equations using Laplace Transforms: x(t) = 3x₁ (t) + 4x2(t) x(t) = -4x₁(t) + 3x2(t) x₁(0) = 1,x2(0) = 0arrow_forward3. Determine the Laplace Transform for the following functions. Show all of your work: 1-t, 0 ≤t<3 a. e(t) = t2, 3≤t<5 4, t≥ 5 b. f(t) = f(tt)e-3(-) cos 4τ drarrow_forward4. Find the inverse Laplace Transform Show all of your work: a. F(s) = = 2s-3 (s²-10s+61)(5-3) se-2s b. G(s) = (s+2)²arrow_forward
- 1. Consider the differential equation, show all of your work: dy =(y2)(y+1) dx a. Determine the equilibrium solutions for the differential equation. b. Where is the differential equation increasing or decreasing? c. Where are the changes in concavity? d. Suppose that y(0)=0, what is the value of y as t goes to infinity?arrow_forward2. Suppose a LC circuit has the following differential equation: q'+4q=6etcos 4t, q(0) = 1 a. Find the function for q(t), use any method that we have studied in the course. b. What is the transient and the steady-state of the circuit?arrow_forward5. Use variation of parameters to find the general solution to the differential equation: y" - 6y' + 9y=e3x Inxarrow_forward
- Let the region R be the area enclosed by the function f(x) = ln (x) + 2 and g(x) = x. Write an integral in terms of x and also an integral in terms of y that would represent the area of the region R. If necessary, round limit values to the nearest thousandth. 5 4 3 2 1 y x 1 2 3 4arrow_forward(28 points) Define T: [0,1] × [−,0] → R3 by T(y, 0) = (cos 0, y, sin 0). Let S be the half-cylinder surface traced out by T. (a) (4 points) Calculate the normal field for S determined by T.arrow_forward(14 points) Let S = {(x, y, z) | z = e−(x²+y²), x² + y² ≤ 1}. The surface is the graph of ze(+2) sitting over the unit disk. = (a) (4 points) What is the boundary OS? Explain briefly. (b) (4 points) Let F(x, y, z) = (e³+2 - 2y, xe³±² + y, e²+y). Calculate the curl V × F.arrow_forward
- (6 points) Let S be the surface z = 1 − x² - y², x² + y² ≤1. The boundary OS of S is the unit circle x² + y² = 1. Let F(x, y, z) = (x², y², z²). Use the Stokes' Theorem to calculate the line integral Hint: First calculate V x F. Jos F F.ds.arrow_forward(28 points) Define T: [0,1] × [−,0] → R3 by T(y, 0) = (cos 0, y, sin 0). Let S be the half-cylinder surface traced out by T. (a) (4 points) Calculate the normal field for S determined by T.arrow_forwardI need the last answer t=? I did got the answer for the first two this is just homework.arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning
Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON
Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning
Calculus: Early Transcendentals
Calculus
ISBN:9781285741550
Author:James Stewart
Publisher:Cengage Learning
Thomas' Calculus (14th Edition)
Calculus
ISBN:9780134438986
Author:Joel R. Hass, Christopher E. Heil, Maurice D. Weir
Publisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)
Calculus
ISBN:9780134763644
Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric Schulz
Publisher:PEARSON
Calculus: Early Transcendentals
Calculus
ISBN:9781319050740
Author:Jon Rogawski, Colin Adams, Robert Franzosa
Publisher:W. H. Freeman
Calculus: Early Transcendental Functions
Calculus
ISBN:9781337552516
Author:Ron Larson, Bruce H. Edwards
Publisher:Cengage Learning
Sine, Cosine and Tangent graphs explained + how to sketch | Math Hacks; Author: Math Hacks;https://www.youtube.com/watch?v=z9mqGopdUQk;License: Standard YouTube License, CC-BY