Chapter 5, Problem 2RCC

a.

To determine

Explain what is even function.

Answer to Problem 2RCC

The even function is a function which satisfy particular symmetry relation, w. r. t. taking additive inverse.

  $f(x)=f(-x)$

  

Explanation of Solution

Let f is a real-valued function of real variable. Then f is even if the following equation hold for all $x$ such that $x$ and $-x$ in the domain of f.

  $f(x)=f(-x)$

We may rewrite the equation as,

  $f(x)-f(-x)=0$

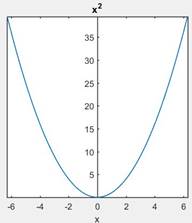
Geographically, the graph of the even function is symmetric w. r. t. y-axis, meaning the graph remain unchanged after reflecting the y-axis.

For example, Let take a function $f(x)=x^2$

Then,

  $f(-x)={\left(-x\right)}^2=x^2$

The function holds the symmetric relation so, it is even function.

Program:

clc
clear
close all
syms x
f=x^2;
p=ezplot(f);
p.LineWidth=1.25;
ax=gca;
set(ax,'linewidth',1.2,'fontsize',12);
ax.XAxisLocation='origin';
ax.YAxisLocation='origin';
axis tight
axis square

Query:

• Fist, we have defined the function.
• Then sketch a graph using “ezplot”.

b.

To determine

Show which trigonometric functions are even.

Answer to Problem 2RCC

The trigonometric functions which are even is,

  $\begin{array}{l}\cos (-x)=\cos x\\ \sec (-x)=\sec x\end{array}$

Explanation of Solution

Calculation:

Let’s take a function,

  $f(x)=\cos x$

As we know that the even function follows the symmetry,

  $f(x)=f(-x)$

Then,

  $f(-x)=\cos (-x)=\cos x$

Similarly, for the $\sec x$ .

  $f(x)=\sec x$

Then,

  $f(-x)=\sec (-x)=\sec x$

Conclusion:

The trigonometric function which are even is,

  $\begin{array}{l}\cos (-x)=\cos x\\ \sec (-x)=\sec x\end{array}$

c.

To determine

Explain what is odd function.

Answer to Problem 2RCC

The odd function is a function which satisfy particular symmetry relation, w. r. t. taking additive inverse.

  $-f(x)=f(-x)$

  

Explanation of Solution

Let f is a real-valued function of real variable. Then f is odd if the following equation hold for all $x$ such that $x$ and $-x$ in the domain of f.

  $-f(x)=f(-x)$

We may rewrite the equation as,

  $f(x)+f(-x)=0$

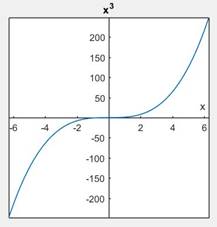
Geographically, the graph of the odd function has rotational symmetric w. r. t. the origin, meaning the graph remain unchanged after rotating 180^o about the origin.

For example, Let take a function $f(x)=x^3$

Then,

  $f(-x)={\left(-x\right)}^3=-x^3$

The function holds the symmetric relation so, it is odd function.

Program:

clc
clear
close all
syms x
f=x^3;
p=ezplot(f);
p.LineWidth=1.25;
ax=gca;
set(ax,'linewidth',1.2,'fontsize',12);
ax.XAxisLocation='origin';
ax.YAxisLocation='origin';
axis tight
axis square

Query:

• Fist, we have defined the function.
• Then sketch a graph using “ezplot”.

d.

To determine

Show which trigonometric functions are odd.

Answer to Problem 2RCC

The trigonometric functions which are even is,

  $\begin{array}{l}\sin (-x)=-\sin x\\ csc(-x)=-\csc (x)\end{array}$

Explanation of Solution

Calculation:

Let’s take a function,

  $f(x)=\sin x$

As we know that the even function follows the symmetry,

  $-f(x)=f(-x)$

Then,

  $f(-x)=\sin (-x)=-\sin x$

Similarly, for the $\csc x$ .

  $f(x)=\csc x$

Then,

  $f(-x)=\csc (-x)=-\csc x$

Conclusion:

The trigonometric function which are even is,

  $\begin{array}{l}\sin (-x)=-\sin x\\ csc(-x)=-\csc (x)\end{array}$