
Concept explainers
Assume the switch in the circuit in Figure P5.69has been closed for a very long lime. It is suddenly opened at
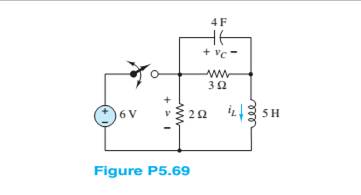
The inductor current
Answer to Problem 5.69HP
Explanation of Solution
Given:
The given circuit is shown below:
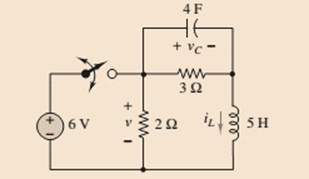
Calculation:
When switch is closed for long time means the circuit is in steady state condition. In this condition the capacitor is open circuited, and inductor is short circuited. Therefore, the modified circuit can be drawn as:
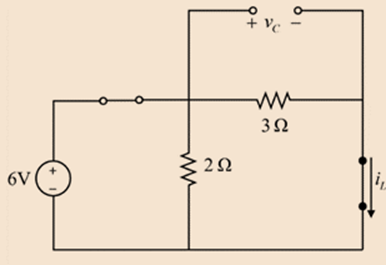
The current through the source just before the opening it at t = 0,
Applying the current division rule, the initial value of the current can be calculated as
The initial value of voltage across the capacitor will be
The switch is opened at t = 0, the circuit can be drawn as
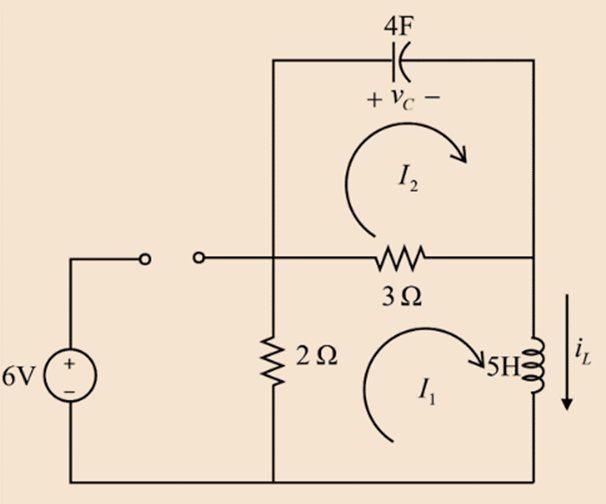
Applying KVL in the loop having current
Applying KVL in the loop having current
Differentiating with respect to t,
Put the value of
Assuming
The auxiliary equation can be written as
The roots can be calculated as
Therefore, the solution of the differential equation will be in the form
Current through the inductor is equal to the loop current,
Using the initial conditions,
At t = 0,
Substituting 0 for t,
Therefore,
Differentiating equation 2 with respect to t,
Substituting 0 for t,
Applying KVL in the loop with current
Substituting the values,
Substituting this in equation 4,
Substituting A and B in equation 2,
Substituting A and B in equation 3,
Put these values in equation 5,
Substitute
Substitute
Reclose the circuit. Now, the initial current in the inductor is represented as a voltage source of
Thus,
The initial voltage across the capacitor is represented as a voltage source of
The circuit can be drawn as
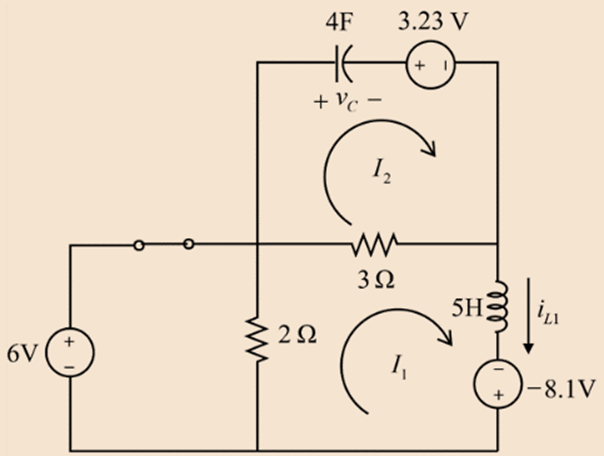
It can be observed that the voltage across the
Apply KVL in the loop with current
Apply KVL in the loop with current
Assuming
The auxiliary equation can be written as
The roots can be calculated as
Therefore, the solution of the differential equation will be in the form
Current through the inductor is equal to the loop current,
Using the initial conditions,
At t = 5,
Substituting 5 for t,
Differentiating equation 8 with respect to t,
Substituting 5 for t,
The voltage across the inductor at t = 5s will be
Substituting this in equation 10,
Substituting A and B in equation 8,
The complete solution can be calculated as
The 6V is always connected across the 2ohm resistor whenever the switch is closed. Therefore, the voltage across the 2ohm resistor will be
When the switch is opened, the current through the inductor flows through the 2ohm resistor. Thus, the voltage across the 2ohm resistor, when the switch is open will be
Substituting the value of
The voltage across the 2ohm resistor will be
Want to see more full solutions like this?
Chapter 5 Solutions
Principles and Applications of Electrical Engineering
- a single circuit 50hz transmission line is 362 km long. the load is125mw at 200kv with 100% power factor. 1. evaluate the incident and reflected voltages at the receiving end of the line and at the sending end of the line. 2. determine the line voltage at the sending end from the incident and reflected voltages. 3. computer the wavelength and velocity of propagation. parameters of the line are r = 0.1069 ohms/km. l=1.355mh/km c=8.452nf/km g=0arrow_forwardQ1. Figure 1 shows a differential amplifier. Assume that all transistors are identical. ẞ=180, V = 0.026 Vand V = 0.7V. a) b) Show that the d.c. bias current to the differential pairs is Iccs = 0.6 mA. Calculate the d.c. voltages at the output terminals V。1 and V02- c) Given that the input signals are v₁ = 4 sin(wt) and V₁₂ = 2sin(wt) in mV, find the a.c. voltage between V01 and V02-arrow_forwardQ1. Figure 1 shows a differential amplifier. Assume that all transistors are identical. ẞ=180, V = 0.026 Vand V = 0.7V. a) b) Show that the d.c. bias current to the differential pairs is Iccs = 0.6 mA. Calculate the d.c. voltages at the output terminals V。1 and V02- c) Given that the input signals are v₁ = 4 sin(wt) and V₁₂ = 2sin(wt) in mV, find the a.c. voltage between V01 and V02-arrow_forward
- Q4 Determine the Y-parameters at a frequency of 10 kHz for the two-port network shown in figure below. Present your answer in matrix form. R1 R3 C3 R5 L5 •w• 5 Ohm ww 4 Ohm 200 μF 5 Ohm 8.4 mH 1 Ohm R2 C4 796 µF 400 μF C2arrow_forwardQ1. Figure 1 shows (a) a differential amplifier and (b) a current mirror. All transistors in the circuit are identical and their parameters are: VBE = 0.7 V, VT = 0.026 V, and ẞ = 150. a) Given that the biasing current of Figure 1(a) is I = 1 mA, determine the dc voltages at the output terminals of the differential amplifier. b) Given that the biasing current of Figure 1(a) is I = 1 mA and the ac input signal is via = 1.5 sin(wt) mv, find the corresponding ac output voltage at terminal vo₁ of the differential amplifier. c) In order to provide an output current of 1 mA using on Figure 1(b), find the value for the resistor, R, in Figure 1(b).arrow_forwardQ2. Two op-amp circuits are shown in Figure 2. One of them is an inverting amplifier and the other is a Schmitt trigger. Assume the op-amps used in both circuits are ideal op-amps. The output of the Schmitt trigger is switching between -12 V and +12V (i.e., Vmax = ±12 V). a) Identify which is the inverting amplifier and which is the Schmitt trigger. b) Use the corresponding circuit diagram in Figure 2 to design an inverting amplifier that has a gain of -20 with the output offset voltage minimised. Determine the values of the resistors. c) Select the corresponding circuit diagram in Figure 2 to design a Schmitt trigger that has a lower trigger level of -1 V and an upper trigger level of +2 V. Determine the values of resistors. Sketch the transfer characteristics of this trigger.arrow_forward
- Q2. A simple comparator and a Schmitt trigger are shown in Figures 2(a) and 2(b). The maximum output voltage, Vmax, can switch between -10 V and +10 V for both circuits. The lower and upper trigger levels of the Schmitt trigger are -1 V and +2 V, respectively. a) Based on the information given above, sketch the transfer characteristics for both circuits. b) Show that the hysteresis of the Schmitt trigger of Figure 2(b) can be expressed as 2. R₁- Vmax Vnys R₁ + R₂ c) Using the parameters provided above, determine the ratio of R₂/R₁ for the circuit of Figure 2(b).arrow_forwardDon't use ai to answer I will report you answerarrow_forward3 phase transformer bank is connected with the primaries in deltas and secondaries in wye. Line voltage of the primary is 120V and secondary side is 240V. Required to find the ratio of primary to secondary turns on each of the single phase transformers.arrow_forward
- A generator delivers power through a transmission line to a star-connected load. The system is balanced. Find the values of the currents involved in per unit, considering: (a) single-phase bases and (b) three-phase bases. Datos: S₁ = 2 MVA Vg = 13.2 kV Generador ++ Linea Demanda Pg+jQg Uga ZLT a Zlinea 8.68+j3.162 Zcarga = 70+/10 la ZDa ZD b ZD€ Bases trifásicas: Ug b ZLT b Sb36 = 2 MVA Vb34 = 13.820° kV Ugo ZLTCarrow_forwardcontrol systemarrow_forwardcontrol systemarrow_forward
 Introductory Circuit Analysis (13th Edition)Electrical EngineeringISBN:9780133923605Author:Robert L. BoylestadPublisher:PEARSON
Introductory Circuit Analysis (13th Edition)Electrical EngineeringISBN:9780133923605Author:Robert L. BoylestadPublisher:PEARSON Delmar's Standard Textbook Of ElectricityElectrical EngineeringISBN:9781337900348Author:Stephen L. HermanPublisher:Cengage Learning
Delmar's Standard Textbook Of ElectricityElectrical EngineeringISBN:9781337900348Author:Stephen L. HermanPublisher:Cengage Learning Programmable Logic ControllersElectrical EngineeringISBN:9780073373843Author:Frank D. PetruzellaPublisher:McGraw-Hill Education
Programmable Logic ControllersElectrical EngineeringISBN:9780073373843Author:Frank D. PetruzellaPublisher:McGraw-Hill Education Fundamentals of Electric CircuitsElectrical EngineeringISBN:9780078028229Author:Charles K Alexander, Matthew SadikuPublisher:McGraw-Hill Education
Fundamentals of Electric CircuitsElectrical EngineeringISBN:9780078028229Author:Charles K Alexander, Matthew SadikuPublisher:McGraw-Hill Education Electric Circuits. (11th Edition)Electrical EngineeringISBN:9780134746968Author:James W. Nilsson, Susan RiedelPublisher:PEARSON
Electric Circuits. (11th Edition)Electrical EngineeringISBN:9780134746968Author:James W. Nilsson, Susan RiedelPublisher:PEARSON Engineering ElectromagneticsElectrical EngineeringISBN:9780078028151Author:Hayt, William H. (william Hart), Jr, BUCK, John A.Publisher:Mcgraw-hill Education,
Engineering ElectromagneticsElectrical EngineeringISBN:9780078028151Author:Hayt, William H. (william Hart), Jr, BUCK, John A.Publisher:Mcgraw-hill Education,





