Chapter 5, Problem 5.65HP

To determine

The current $i_1$ through $R_1$ and the value of the current and the voltage $v_2$ across the resistance $R_2$ for $t=\infty$ .

Answer to Problem 5.65HP

The value of current $i_1$ through $R_1$ for time $t=\infty$ is $0\text{A}$ and the voltage $v_2$ across the resistance $R_2$ for time $t=\infty$ is $0\text{V}$ .

Explanation of Solution

Calculation:

The given diagram is shown in Figure 1

  

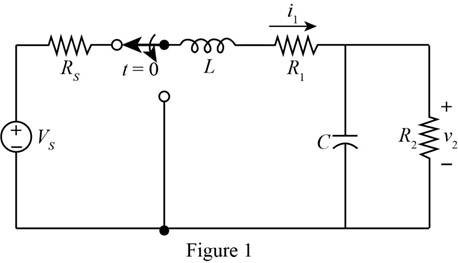
The conversion from $\mu \text{F}$ into $\text{F}$ is given by

  $1\mu \text{F}={10}^{-6}\text{F}$

The conversion from $0.5\mu \text{F}$ into $\text{F}$ is given by,

  $0.5\mu \text{F}=0.5\times {10}^{-6}\text{F}$

The conversion from $1\text{mH}$ into $\text{H}$ is given by,

  $1\text{mH}={10}^{-3}\text{H}$

The conversion from $0.9\text{mH}$ into $\text{H}$ is given by,

  $0.9\text{mH}=0.9\times {10}^{-3}\text{H}$

The conversion from $\text{k}\Omega$ into $\Omega$ is given by,

  $\text{1}\text{k}\Omega ={10}^3\Omega$

The conversion from $31\text{k}\Omega$ into $\Omega$ is given by,

  $31\text{k}\Omega =31\times {10}^3\Omega$

The conversion from $22\text{k}\Omega$ into $\Omega$ is given by,

  $22\text{k}\Omega =22\times {10}^3\Omega$

For time $t=0^{-}$ the circuit reaches a state reaches a steady state, the capacitor acts as an open circuit and the inductor as a short circuit. Mark the values and redraw the circuit.

The required diagram is shown in Figure 2

  

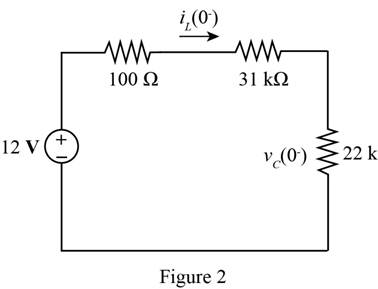
From above, the expression for the current $i_L\left(0^{-}\right)$ is given by,

  $\begin{array}{c}{i}_L\left(0^{-}\right)=\frac{12\text{V}}{100\Omega +30\times {10}^3\Omega +22\times {10}^3\Omega }\\ =225.989\times {10}^{-6}\text{A}\end{array}$

The inductor opposes the sudden change in the current, thus the current $i_L\left(0\right)$ is given by,

  $i_L\left(0\right)=i_L\left(0^{-}\right)$

Substitute $225.989\times {10}^{-6}\text{A}$ for $i_L\left(0^{-}\right)$ in the above equation.

  $i_L\left(0\right)=225.989\times {10}^{-6}\text{A}$

The expression for the voltage across the capacitor for time $t=0^{-}$ is given by,

  $v_C\left(0^{-}\right)=i_L\left(0^{-}\right)R_2$

Substitute $225.989\times {10}^{-6}\text{A}$ for $i_L\left(0^{-}\right)$ and $\left(22\times {10}^3\Omega \right)$ for $R_2$ in the above equation.

  $\begin{array}{c}{v}_C\left(0^{-}\right)=\left(225.989\times {10}^{-6}\text{A}\right)\left(22\times {10}^3\Omega \right)\\ =4.97\text{V}\end{array}$

The expression for the voltage across the capacitor for time $t=0^{+}$ is given by,

  $v_C\left(0^{+}\right)=v_C\left(0^{-}\right)$

Substitute $4.97\text{V}$ for $v_C\left(0^{-}\right)$ in the above equation.

  $v_C\left(0^{+}\right)=4.97\text{V}$

The capacitor opposes the sudden change in the voltage and acts as a short circuit. Change the switch position, mark the values and redraw the circuit for $t>0$ .

The required diagram is shown in Figure 3

  

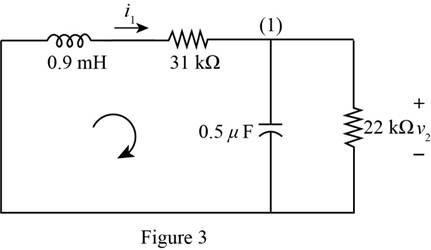
Apply KCL to the top node of the above circuit.

  $\begin{array}{l}{i}_1=C\frac{d{v}_2}{dt}+\frac{v_2}{R_2}\\ \frac{i_1\left(t\right)}{C}-\frac{v_2\left(t\right)}{R_{2}C}=\frac{d{v}_2}{dt}\end{array}$  ........(1)

Apply KVL in the left loop of the above circuit.

  $L\frac{d{i}_1}{dt}+R_1{i}_1+v_2=0$

Substitute $C\frac{d{v}_2}{dt}+\frac{v_2}{R_2}$ for $i_1$ in the above equation.

  $\begin{array}{l}L\frac{d}{dt}\left[C\frac{d{v}_2}{dt}+\frac{v_2}{R_2}\right]+R_1\left(C\frac{d{v}_2}{dt}+\frac{v_2}{R_2}\right)+v_2=0\\ LC\frac{d^2{v}_2}{d{t}^2}+\left(\frac{L}{R_2}+R_{1}C\right)\frac{d{v}_2}{dt}+\left(\frac{R_1}{R_2}+1\right)v_2=0\end{array}$

Substitute $0.9\times {10}^{-3}\text{H}$ for $L$, $0.5\times {10}^{-6}\text{F}$ for $C$, $31\times {10}^3\Omega$ for $R_1$ and $22\times {10}^3\Omega$ for $R_2$ in the above equation.

  $\begin{array}{l}\left[\begin{array}{l}\left(0.9\times {10}^{-3}\text{H}\right)\left(0.5\times {10}^{-6}\text{F}\right)\frac{d^2{v}_2}{d{t}^2}+\left(\frac{\left(0.9\times {10}^{-3}\text{H}\right)}{\left(22\times {10}^3\Omega \right)}+\left(31\times {10}^3\Omega \right)\left(0.5\times {10}^{-6}\text{F}\right)\right)\frac{d{v}_2}{dt}\\ +\left(\frac{31\times {10}^3\Omega }{22\times {10}^3\Omega }+1\right)v_2\end{array}\right]=0\\ 4.5\times {10}^{-10}\frac{d^2{v}_2}{d{t}^2}+0.0155\frac{d{v}_2}{dt}+2.409v_2=0\\ \frac{d^2{v}_2}{d{t}^2}+\frac{0.0155}{4.5\times {10}^{-10}}\frac{d{v}_2}{dt}+\frac{2.409v_2}{4.5\times {10}^{-10}}=0\\ \frac{d^2{v}_2}{d{t}^2}+\left(3.44\times {10}^7\right)\frac{d{v}_2}{dt}+\left(5.353\times {10}^9\right)v_2=0\end{array}$

The roots of the above differential equation are given by,

  $\begin{array}{c}{s}_{1,2}=\frac{-3.44\times {10}^{-7}\pm \sqrt{{\left(3.44\times {10}^7\right)}^2-4\left(1\right)\left(5.353\times {10}^9\right)}}{2(1)}\\ =-155.611,-3.439\times {10}^7\end{array}$

The expression for the voltage $v_2$ in terms of the solution of the differential equation is given by,

  $v_2\left(t\right)={\alpha }_1{e}^{s_{1}t}+{\alpha }_2{e}^{s_{2}t}$

Substitute $-155.611$ for $s_1$ and $-3.439\times {10}^7$ for $s_2$ in the above equation.

  $v_2\left(t\right)={\alpha }_1{e}^{-155.611t}+{\alpha }_2{e}^{-3.439\times {10}^{7}t}$  ........(2)

Substitute $0$ for $t$ in the above equation.

  $\begin{array}{c}{v}_2\left(0\right)={\alpha }_1{e}^{-155.611\left(0\right)}+{\alpha }_2{e}^{-3.439\times {10}^7\left(0\right)}\\ ={\alpha }_1+{\alpha }_2\end{array}$

Substitute $4.97\text{V}$ for $v_2\left(0\right)$ in the above equation.

  $4.97\text{V}={\alpha }_1+{\alpha }_2$  ........(3)

The differentiation of $v\left(t\right)$ with respect to $t$ is given by,

  $\frac{dv}{dt}=-155.611{\alpha }_1{e}^{-155.611t}-\left(3.439\times {10}^7\right){\alpha }_2{e}^{-3.439\times {10}^{7}t}$

Substitute $0$ for $t$ in the above equation.

  $\begin{array}{c}\frac{dv}{dt}=-155.611{\alpha }_1{e}^{-155.611\left(0\right)}-\left(3.439\times {10}^7\right){\alpha }_2{e}^{-3.439\times {10}^7\left(0\right)}\\ =-155.611{\alpha }_1-\left(3.439\times {10}^7\right){\alpha }_2\end{array}$

Substitute $0$ for $t$ in equation (1).

  $\frac{i_1\left(0\right)}{C}-\frac{v_2\left(0\right)}{R_{2}C}=\frac{d{v}_2}{dt}$

Substitute $-155.611{\alpha }_1-\left(3.439\times {10}^7\right){\alpha }_2$ for $\frac{d{v}_2}{dt}$ in the above equation.

  $\frac{i_1\left(0\right)}{C}-\frac{v_2\left(0\right)}{R_{2}C}=-155.611{\alpha }_1-\left(3.439\times {10}^7\right){\alpha }_2$

Substitute $225.989\times {10}^{-6}\text{A}$ for $i_1\left(0^{-}\right)$, $4.97\text{V}$ for $v_2\left(0\right)$, $0.5\times {10}^{-6}\text{F}$ for $C$, $22\times {10}^3\Omega$ for $R_2$ and $0.5\times {10}^{-6}\text{F}$ for $C$ in the above equation.

  $\begin{array}{l}\frac{225.989\times {10}^{-6}\text{A}}{\left(0.5\times {10}^{-6}\text{F}\right)}-\frac{4.97\text{V}}{\left(22\times {10}^3\Omega \right)\left(0.5\times {10}^{-6}\text{F}\right)}=-155.611{\alpha }_1-\left(3.439\times {10}^7\right){\alpha }_2\\ 0.1598{\alpha }_1=-155.611{\alpha }_1-\left(3.439\times {10}^7\right){\alpha }_2\end{array}$

From above and from equation (3), the evaluated value of the constant ${\alpha }_1$ and ${\alpha }_2$ is given by,

  $\begin{array}{l}{\alpha }_1=4.97\\ {\alpha }_2=-2.249\times {10}^{-5}\end{array}$

Substitute $4.97$ for ${\alpha }_1$ and $-2.249\times {10}^{-5}$ for ${\alpha }_2$ in equation (2)

  $v_2\left(t\right)=\left(4.97\right)e^{-155.611t}-\left(2.249\times {10}^{-5}\right)e^{-3.439\times {10}^{7}t}$

Substitute $\infty$ for $t$ in the above equation.

  $\begin{array}{c}{v}_2\left(\infty \right)=\left(4.97\right)e^{-155.611\left(\infty \right)}-\left(2.249\times {10}^{-5}\right)e^{-3.439\times {10}^7\left(\infty \right)}\\ =0\text{V}\end{array}$

Substitute $\left(4.97\right)e^{-155.611t}-\left(2.249\times {10}^{-5}\right)e^{-3.439\times {10}^{7}t}$ for $v_2\left(t\right)$ in the above equation.

  $i_1\left(t\right)=\left[\begin{array}{l}C\frac{d\left[\left(4.97\right)e^{-155.611t}-\left(2.249\times {10}^{-5}\right)e^{-3.439\times {10}^{7}t}\right]}{dt}\\ +\frac{\left[\left(4.97\right)e^{-155.611t}-\left(2.249\times {10}^{-5}\right)e^{-3.439\times {10}^{7}t}\right]}{R_2}\end{array}\right]$

Substitute $0.5\times {10}^{-6}\text{F}$ for $C$ and $22\times {10}^3\Omega$ for $R_2$ in the above equation.

  $\begin{array}{c}{i}_1\left(t\right)=\left[\begin{array}{l}\left(0.5\times {10}^{-6}\text{F}\right)\frac{d\left[\left(4.97\right)e^{-155.611t}-\left(2.249\times {10}^{-5}\right)e^{-3.439\times {10}^{7}t}\right]}{dt}\\ +\frac{\left[\left(4.97\right)e^{-155.611t}-\left(2.249\times {10}^{-5}\right)e^{-3.439\times {10}^{7}t}\right]}{22\times {10}^3\Omega }\end{array}\right]\\ =\left[\begin{array}{l}\left(0.5\times {10}^{-6}\text{F}\right)\left(\left(4.97\right)e^{-155.611t}-\left(2.249\times {10}^{-5}\right)e^{-3.439\times {10}^{7}t}\right)\\ +\frac{\left(4.97\right)e^{-155.611t}-\left(2.249\times {10}^{-5}\right)e^{-3.439\times {10}^{7}t}}{22\times {10}^3\Omega }\end{array}\right]\end{array}$

Substitute $\infty$ for $t$ in the above equation.

  $\begin{array}{c}{i}_1\left(\infty \right)=\left[\begin{array}{l}\left(0.5\times {10}^{-6}\text{F}\right)\left(\left(4.97\right)e^{-155.611\left(\infty \right)}-\left(2.249\times {10}^{-5}\right)e^{-3.439\times {10}^7\left(\infty \right)}\right)\\ +\frac{\left(4.97\right)e^{-155.611\left(\infty \right)}-\left(2.249\times {10}^{-5}\right)e^{-3.439\times {10}^7\left(\infty \right)}}{22\times {10}^3\Omega }\end{array}\right]\\ =0\end{array}$

Conclusion:

Therefore, the value of current $i_1$ through $R_1$ for time $t=\infty$ is $0\text{A}$ and the voltage $v_2$ across the resistance $R_2$ for time $t=\infty$ is $0\text{V}$ .