Chapter 5, Problem 5.72HP

To determine

The inductor current I_L, voltage 'v' across the 2Ω resister and voltage $v_c$ across capacitor for $t\ge 0$ .

Answer to Problem 5.72HP

  $\begin{array}{l}{i}_L\left(t\right)=\left(2.748-j7.67\right)e^{\left(-0.24167+j0.157\right)\left(t-5\right)}+\left(-0.248+j8.41\right)e^{\left(-0.24167-j0.157\right)\left(t-5\right)}\text{A}\\ v=\left(5.496-j15.34\right)e^{\left(-0.24167+j0.157\right)\left(t-5\right)}+\left(-0.496+j16.82\right)e^{\left(-0.24167-j0.157\right)\left(t-5\right)}\text{V}\\ v_c\left(t\right)==\left(2.796-j26.765\right)e^{\left(-0.24167+j0.157\right)\left(t-5\right)}+\left(-6.796+27.17\right)e^{\left(-0.24167-j0.157\right)\left(t-5\right)}\end{array}$

Explanation of Solution

Given:

The given circuit is shown below.

  

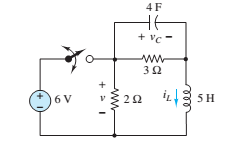
The switch is closed at t = 0 s and reopened at t = 5 s.

Calculation:

The capacitor does not allow the sudden change in voltage and the inductor does not allow the sudden change in current.

At t = 0, the capacitor behaves like short circuit and inductor behaves like open circuit.

The modified circuit diagram is:

  

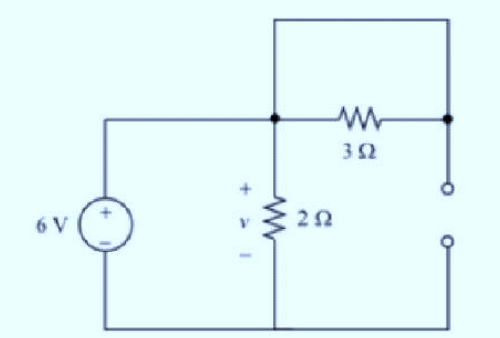
From the circuit,

  $V_L\left(0\right)=6\text{V}$

Relation between inductor current and voltage is:

  $\begin{array}{l}V\left(0\right)=L\frac{di\left(0\right)}{dt}\\ \frac{di\left(0\right)}{dt}=\frac{V\left(0\right)}{L}\\ =\frac{6}{5}\\ =1.2\frac{\text{A}}{\text{s}}\end{array}$

Considering the following circuit, at $t>0$:

  

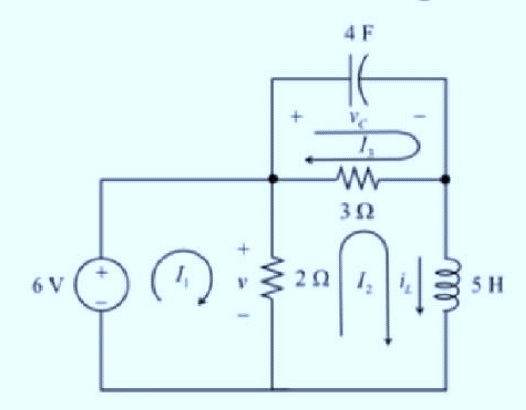
Applying Kirchhoff's voltage law in loop1,

  $\begin{array}{l}-6+\left(2\right)\left(I_1-I_2\right)=0\\ 2\left(I_1-I_2\right)=6\\ I_1-I_2=3\\ I_1=3+I_2\mathrm{.....}\left(1\right)\end{array}$

Applying Kirchhoff's voltage law in top loop,

  $3\left(I_3-I_2\right)+\frac{1}{4}{\displaystyle \int I_{3}dt}=0$

Differentiating the equation with respect to t,

  $\begin{array}{l}3D\left(I_3-I_2\right)+\frac{I_3}{4}=0\\ 3D{I}_3+0.25I_3=3D{I}_2\\ I_3=\frac{3D{I}_2}{3D+0.25}\mathrm{....}\left(2\right)\end{array}$

Applying Kirchhoff's voltage law in bottom loop,

  $2\left(I_2-I_1\right)+3\left(I_2-I_3\right)+5\left(D{I}_2\right)=0$

From equation 1, putting the value of $I_1$ ,

  $\begin{array}{l}2\left(I_2-3-I_2\right)+3\left(I_2-I_3\right)+5\left(D{I}_2\right)=0\\ 3I_2-3I_3+5D{I}_2=6\end{array}$

From equation 2, putting the value of $I_3$ ,

  $\begin{array}{l}3I_2-3\left[\frac{3D{I}_2}{3D+0.25}\right]+5D{I}_2=6\\ 3I_2\left(3D+0.25\right)-9D{I}_2+5D{I}_2\left(3D+0.25\right)=6\left(3D+0.25\right)\\ 9D{I}_2+0.75I_2-9D{I}_2+15D^2{I}_2+1.25D{I}_2=18D+1.5\end{array}$

Differentiation of any constant value is zero.

  $18D=0$

  $15D^2{I}_2+1.25D{I}_2+0.75I_2=1.5$

Writing the equation in standard second order differential equation:

Dividing by 0.75,

  $20D^2{I}_2+1.67D{I}_2+I_2=2$

Comparing the equation with standard second order differential equation:

  $LC\left(D^2\right)I_2+\frac{L}{R}\left(D\right)I_2+I_2=Kf\left(t\right)$

The natural frequency is determined as:

  $\begin{array}{l}{\omega }_n=\sqrt{\frac{1}{LC}}\\ =\sqrt{\frac{1}{20}}\\ =0.2236\raisebox{1ex}{$\text{rad}$}\!\left/ \!\raisebox{-1ex}{$\text{s}$}\right.\end{array}$

The damping ratio is determined as follows:

  $\begin{array}{l}\frac{2\xi }{{\omega }_n}=\frac{L}{R}\\ \frac{2\xi }{0.2236}=1.67\\ 2\xi =0.372\\ \xi =0.186\end{array}$

The value of damping ratio is less than 1.

  $\xi <1$

Hence, it is an underdamped second order circuit.

The following expression is used to solve the complete solution.

  $\begin{array}{l}{i}_L\left(t\right)=i_{LN}\left(t\right)+i_{LF}\left(t\right)\\ ={\alpha }_1{e}^{s_{1}t}+{\alpha }_2{e}^{s_{2}t}+i_L\left(\infty \right)\end{array}$

  $i_{LN}\left(t\right)$ =natural response

  $i_{LF}\left(t\right)$ =forced response

The roots $s_{1,2}$ are:

  $\begin{array}{l}{s}_{1,2}=-\xi {\omega }_n\pm j{\omega }_n\sqrt{1-{\xi }^2}\\ =-\left(0.186\right)\left(0.2236\right)\pm j\left(0.2236\right)\sqrt{1-{0.186}^2}\\ =-0.04167\pm j0.2196\end{array}$

At t = 0, the inductor's natural response current is zero.

  $\begin{array}{l}{i}_{LN}\left(0\right)={\alpha }_1{e}^{s_1\left(0\right)}+{\alpha }_2{e}^{s_2\left(0\right)}\\ 0={\alpha }_1+{\alpha }_2\\ {\alpha }_1=-{\alpha }_2\end{array}$

Differentiating the above equation and substituting t = 0,

  $\begin{array}{l}D{i}_{LN}\left(0\right)=s_1{\alpha }_1{e}^{s_1\left(0\right)}+s_2{\alpha }_2{e}^{s_2\left(0\right)}\\ 1.2=s_1{\alpha }_1+s_2{\alpha }_2\end{array}$

Substituting, $s_{1,2}=-0.04167\pm j0.2196$ and ${\alpha }_1=-{\alpha }_2$ :

  $\begin{array}{l}1.2=\left(-0.04167+j0.2196\right)\left(-{\alpha }_2\right)+\left(-0.04167-j0.2196\right){\alpha }_2\\ 1.2=0.04167{\alpha }_2-j0.2196{\alpha }_2-0.04167{\alpha }_2-j0.2196{\alpha }_2\\ 1.2=-j0.4393{\alpha }_2\\ {\alpha }_2=\frac{1.2}{-j0.4393}\\ =j2.73\\ {\alpha }_1=-j2.73\end{array}$

Thus, expression for inductor current is:

  $i_L\left(t\right)=-j2.73e^{\left(-0.04167+j0.2196\right)t}+j2.73e^{\left(-0.04167-j0.2196\right)t}\text{A}$

The voltage across the inductor is:

  $\begin{array}{l}{v}_L\left(t\right)=L\frac{d{i}_L\left(t\right)}{dt}\\ =5\frac{d}{dt}\left[-j2.73e^{\left(-0.04167+j0.2196\right)t}+j2.73e^{\left(-0.04167-j0.2196\right)t}\text{A}\right]\\ =5\left[\begin{array}{l}\left(-j2.73\right)\left(-0.04167+j0.2196\right)e^{\left(-0.04167+j0.2196\right)t}+\\ \left(j2.73\right)\left(-0.04167-j0.2196\right)e^{\left(-0.04167-j0.2196\right)t}\end{array}\right]\\ =5\left[\begin{array}{l}\left(0.6+j0.11\right)e^{\left(-0.04167+j0.2196\right)t}+\\ \left(0.6-j0.11\right)e^{\left(-0.04167-j0.2196\right)t}\end{array}\right]\text{V}\end{array}$

The voltage across the resistor is:

  $\begin{array}{l}v=2\left(I_1-I_2\right)\\ =2\left(3+I_2-I_2\right)\\ =6\text{V}\end{array}$

The voltage across the capacitor is:

  $\begin{array}{l}{v}_C\left(t\right)=v-v_L\\ =6-5\left[\begin{array}{l}\left(0.6+j0.11\right)e^{\left(-0.04167+j0.2196\right)t}+\\ \left(0.6-j0.11\right)e^{\left(-0.04167-j0.2196\right)t}\end{array}\right]\text{V}\\ =6-\left[\begin{array}{l}\left(2.997+j0.568\right)e^{\left(-0.04167+j0.2196\right)t}+\\ \left(2.997-j0.568\right)e^{\left(-0.04167-j0.2196\right)t}\end{array}\right]\text{V}\end{array}$

Considering that at t = 5 s, the switch moved to open position.

The initial value of the inductor current is:

  $\begin{array}{l}{i}_L\left(5\right)=-j2.73e^{\left(-0.04167+j0.2196\right)\left(5\right)}+j2.73e^{\left(-0.04167-j0.2196\right)\left(5\right)}\text{A}\\ =-j2.73e^{-0.20835}{e}^{j1.098}+j2.73e^{-0.20835}{e}^{-j1.098}\\ =-j2.73\left(0.812\right)\left(0.455+j0.89\right)+j2.73\left(0.812\right)\left(0.455-j0.89\right)\\ =2.5+j0.74\text{A}\end{array}$

The initial value of the capacitor voltage is:

  $\begin{array}{l}{v}_c\left(5\right)=6-\left[\begin{array}{l}\left(2.997+j0.568\right)e^{\left(-0.04167+j0.2196\right)5}+\\ \left(2.997-j0.568\right)e^{\left(-0.04167-j0.2196\right)5}\end{array}\right]\text{V}\\ =6-\left[\begin{array}{l}\left(2.997+j0.568\right)e^{-0.20835}{e}^{j1.098}+\\ \left(2.997-j0.568\right)e^{-0.20835}{e}^{-j1.098}\end{array}\right]\\ =6-\left[\begin{array}{l}\left(2.997+j0.568\right)\left(0.812\right)\left(0.455+j0.89\right)\\ +\left(2.997-j0.568\right)\left(0.812\right)\left(0.455-j0.89\right)\end{array}\right]\\ =6-1.39-j0.005\\ =4.6-0.005\text{V}\end{array}$

Considering the following circuit to determine the initial values:

  

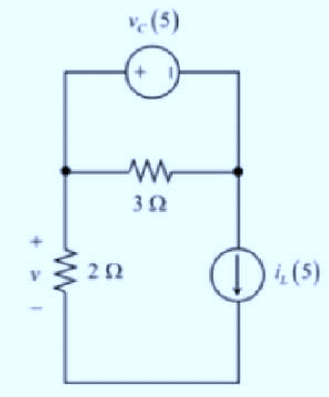
The inductor voltage:

  $\begin{array}{l}{v}_L\left(5\right)=2i_L\left(5\right)+v_C\\ =2\left(2.5+j0.74\right)+\left(4.6-j0.005\right)\\ =9.6+j1.475\text{V}\end{array}$

  $\begin{array}{l}{v}_L\left(5\right)=L\frac{d{i}_L\left(5\right)}{dt}\\ \frac{d{i}_L\left(5\right)}{dt}=\frac{v_L\left(5\right)}{L}\\ =\frac{9.6+j1.475}{5}\\ =1.92+j0.295\frac{A}{s}\end{array}$

Considering the following circuit for t > 5 s.

  

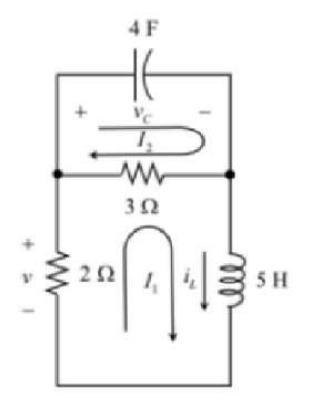
Applying Kirchhoff's voltage law in top loop,

  $3\left(I_2-I_1\right)+\frac{1}{4}{\displaystyle \int I_{2}dt}=0$

Differentiating the equation with respect to t,

  $\begin{array}{l}3D\left(I_2-I_1\right)+\frac{I_2}{4}=0\\ 3D{I}_2+0.25I_2=3D{I}_1\\ I_2=\frac{3D{I}_1}{3D+0.25}\end{array}$

Applying Kirchhoff's voltage law in bottom loop,

  $\begin{array}{l}2I_1+3\left(I_1-I_2\right)+5D\left(I_1\right)=0\\ 5I_1-3I_2+5D{I}_1=0\\ 5I_1-3\left(\frac{3D}{3D+0.25}\right)I_1+5D{I}_1=0\\ 5I_1\left(3D+0.25\right)-9D{I}_1+5D{I}_1\left(3D+0.25\right)=0\\ 15D^2{I}_1+7.25I_1+1.25I_1=0\\ 12D^2{I}_1+5.8D{I}_1+I_1=0\end{array}$

Comparing with standard second order equation:

  $LC\left(D^2\right)I_2+\frac{L}{R}\left(D\right)I_2+I_2=0$

The natural frequency is determined as:

  $\begin{array}{l}{\omega }_n=\sqrt{\frac{1}{LC}}\\ =\sqrt{\frac{1}{12}}\\ =0.2886\raisebox{1ex}{$\text{rad}$}\!\left/ \!\raisebox{-1ex}{$\text{s}$}\right.\end{array}$

The damping ratio is determined as follows:

  $\begin{array}{l}\frac{2\xi }{{\omega }_n}=\frac{L}{R}\\ \frac{2\xi }{0.2886}=5.8\\ 2\xi =1.674\\ \xi =0.837\end{array}$

The value of damping ratio is less than 1.

  $\xi <1$

Hence, it is an underdamped second order circuit.

The following expression is used to determine the complete solution:

  $\begin{array}{l}{i}_L\left(t\right)={\alpha }_1{e}^{s_1\left(t-5\right)}+{\alpha }_2{e}^{s_2\left(t-5\right)}\\ 2.5+j0.74={\alpha }_1+{\alpha }_2\\ {\alpha }_1=2.5+j0.74-{\alpha }_2\end{array}$

  $\begin{array}{l}{i}_L\left(t\right)={\alpha }_1{e}^{s_1\left(t-5\right)}+{\alpha }_2{e}^{s_2\left(t-5\right)}\\ D{i}_L\left(t\right)={\alpha }_1{s}_1{e}^{s_1\left(t-5\right)}+{\alpha }_2{s}_2{e}^{s_2\left(t-5\right)}\\ D{i}_L\left(5\right)={\alpha }_1{s}_1+{\alpha }_2{s}_2\\ \mathrm{1.92.}j0.295={\alpha }_1{s}_1+{\alpha }_2{s}_2\end{array}$

The roots $s_{1,2}$ are:

  $\begin{array}{l}{s}_{1,2}=-\xi {\omega }_n\pm j{\omega }_n\sqrt{1-{\xi }^2}\\ =-\left(0.837\right)\left(0.2886\right)\pm j\left(0.2886\right)\sqrt{1-{0.837}^2}\\ =-0.24167\pm j0.157\end{array}$

Substituting $-0.24167\pm j0.157$ for s_1,2 and ${\alpha }_1=2.5+j0.74-{\alpha }_2$ ,

  $\begin{array}{l}1.92+j0.295=\left(-0.24167+j0.157\right)\left(2.5+j0.74-{\alpha }_2\right)\\ +\left(-0.24167-j0.157\right){\alpha }_2\\ {\alpha }_2=\frac{2.64+j0.078}{-j0.314}\\ =-0.248+j8.41\\ {\alpha }_1=2.5+j0.74-{\alpha }_2\\ =2.748-j7.67\end{array}$

Hence, the expression of inductor current is:

  $i_L\left(t-5\right)=\left(2.748-j7.67\right)e^{\left(-0.24167+j0.157\right)\left(t-5\right)}+\left(-0.248+j8.41\right)e^{\left(-0.24167-j0.157\right)\left(t-5\right)}\text{A}$

The voltage of inductor is:

  $\begin{array}{l}{v}_L\left(t\right)=L\frac{d{i}_L\left(t\right)}{dt}\\ =5\frac{d}{dt}\left[\begin{array}{l}\left(2.748-j7.67\right)e^{\left(-0.24167+j0.157\right)\left(t-5\right)}+\\ \left(-0.248+j8.41\right)e^{\left(-0.24167-j0.157\right)\left(t-5\right)}\end{array}\right]\\ =5\left[\begin{array}{l}\left(2.748-j7.67\right)\left(-0.24167+j0.157\right)e^{\left(-0.24167+j0.157\right)\left(t-5\right)}+\\ \left(-0.248+j8.41\right)\left(-0.24167-j0.157\right)e^{\left(-0.24167-j0.157\right)\left(t-5\right)}\end{array}\right]\\ =5\left[\left(0.54+j2.285\right)e^{\left(-0.24167+j0.157\right)\left(t-5\right)}+\left(1.26-j2.07\right)e^{\left(-0.24167-j0.157\right)\left(t-5\right)}\right]\text{V}\end{array}$

The voltage of 2O resistor:

  $\begin{array}{l}v=2I_1\\ v=2\left(2.748-j7.67\right)e^{\left(-0.24167+j0.157\right)\left(t-5\right)}+2\left(-0.248+j8.41\right)e^{\left(-0.24167-j0.157\right)\left(t-5\right)}\text{V}\\ v=\left(5.496-j15.34\right)e^{\left(-0.24167+j0.157\right)\left(t-5\right)}+\left(-0.496+j16.82\right)e^{\left(-0.24167-j0.157\right)\left(t-5\right)}\text{V}\end{array}$

The voltage across capacitor is:

  $\begin{array}{l}{v}_c=v-v_L\\ =\left(5.496-j15.34\right)e^{\left(-0.24167+j0.157\right)\left(t-5\right)}+\left(-0.496+j16.82\right)e^{\left(-0.24167-j0.157\right)\left(t-5\right)}\\ -5\left[\left(0.54+j2.285\right)e^{\left(-0.24167+j0.157\right)\left(t-5\right)}+\left(1.26-j2.07\right)e^{\left(-0.24167-j0.157\right)\left(t-5\right)}\right]\\ =\left(2.796-j26.765\right)e^{\left(-0.24167+j0.157\right)\left(t-5\right)}+\left(-6.796+27.17\right)e^{\left(-0.24167-j0.157\right)\left(t-5\right)}\end{array}$