Chapter 5, Problem 5.10.1P

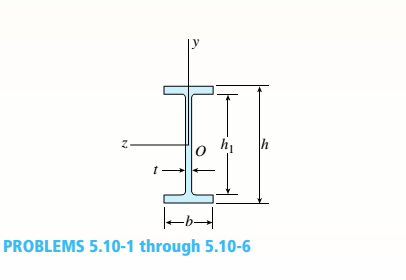
-1 through 5.10-6 A wide-flange beam (see figure) is subjected to a shear force V. Using the dimensions of the cross section, calculate the moment of inertia and then determine the following quantities:

1. The maximum shear stress t_inixin the web.

The minimum shear stress r_min in the web.

The average shear stress t (obtained by dividing the shear force by the area of the web) and the ratio t_max/t_aver.

The shear force Vweb/V carried in the web and the V_web/V.

Note: Disregard the fillets at the junctions of the web and flanges and determine all quantities, including the moment of inertia, by considering the cross section to consist of three rectangles.

5.10-1 Dimensions of cross section: b = 6 in,, ï = 0.5 in., h = 12 in,, A, = 10.5 in., and V = 30 k.

  

To determine

To Find:

The moment of inertia and the maximum shear stress in the web.

Answer to Problem 5.10.1P

The maximum shear stress is ${\tau }_{\max }=5.795\text{ ksi}$ and moment of inertia is $I=333.422{\text{ in}}^{\text{4}}$ .

Explanation of Solution

Given Information:

Shear Force $V=30\text{ k}$

Dimensions,

  $\begin{array}{l}b=6\text{ in}\text{.}\\ t=0.5\text{ in}\text{.}\\ h=12\text{ in}\text{.}\\ h_1=10.5\text{ in}\text{.}\end{array}$

Concept Used:

Following formula will be used

Maximum shear stress, $\tau =\frac{VQ}{Ib}$ .

Moment of inertia of rectangle, $I=\frac{b{h}^3}{12}$ .

Calculation:

Area of upper and lower flanges,

$A_1=b\left(\frac{h}{2}-\frac{h_1}{2}\right)=A_3$

Total area of cross section:

  $\begin{array}{l}A=A_1+A_3+t\times h_1\\ A=2b\left(\frac{h}{2}-\frac{h_1}{2}\right)+t\times h_1\\ A=b(h-h_1)+t\times h_1\\ A=6(12-10.5)+0.5\times 10.5=14.25{\text{ in}}^{\text{2}}\end{array}$

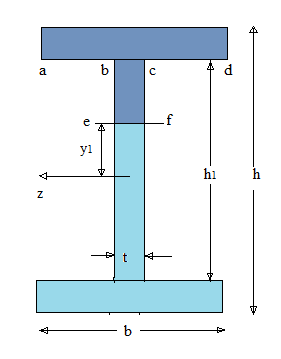
Second rectangle is $efcb$

  $A_2=t\left(\frac{h_1}{2}-y_1\right)$

In which $y_1$ is the distance from neutral axis to line $ef.$

The first moment of areas of $A_1\text{ and }{A}_2$ about the neutral axis

  $Q=A_1\left(\frac{h_1}{2}+\frac{h/2-h_1/2}{2}\right)+A_2\left(y_1+\frac{h_1/2-y_1}{2}\right)$

By putting the values of $A_1\text{ and }{A}_2,$ we get:

$\begin{array}{l}Q=\frac{b}{8}\left(h^2-h_1{}^2\right)+\frac{t}{8}\left(h_1{}^2-4y_1{}^2\right)\\ \text{So},\\ \tau =\frac{VQ}{It}=\frac{V}{It}\left[\frac{b}{8}\left(h^2-h_1{}^2\right)+\frac{t}{8}\left(h_1{}^2-4y_1{}^2\right)\right]\mathrm{...}\text{(1)}\end{array}$

The moment of inertia for the I section is given by following formula:

  $\begin{array}{l}I=\frac{b{h}^3}{12}-\frac{b{h}_1{}^3}{12}+\frac{t{h}_1{}^3}{12}\text{ about the neutral z axis}\text{.}\\ I=\frac{6\times {12}^3}{12}-\frac{6\times {10.5}^3}{12}+\frac{0.5\times {10.5}^3}{12}\\ I=333.422{\text{ in}}^{\text{4}}\end{array}$

The maximum value of shear stress will be at neutral axis when $\begin{array}{l}\\ y_1=0\end{array}$

  $\begin{array}{l}{\tau }_{\max }=\frac{VQ}{It}=\frac{V}{It}\left[\frac{b}{8}\left(h^2-h_1{}^2\right)+\frac{t}{8}\left(h_1{}^2-4y_1{}^2\right)\right]\mathrm{...}\text{(1)}\\ {\tau }_{\max }=\frac{30}{333.422\times 0.5}\left[\frac{6}{8}\left({12}^2-{10.5}^2\right)+\frac{0.5}{8}\left({10.5}^2-0^2\right)\right]\\ {\tau }_{\max }=5.795\text{ ksi}\end{array}$

Conclusion:

The maximum shear stress in the web is ${\tau }_{\max }=5.795\text{ ksi}$ and moment of inertia is $I=333.422{\text{ in}}^{\text{4}}$ .

To determine

To Find:

The minimum shear stress in web.

Answer to Problem 5.10.1P

The minimum shear stress in the web is = ${\tau }_{\min }=4.555\text{ ksi}$ .

Explanation of Solution

Given Information:

Shear Force $V=30\text{ k}$

Dimensions,

  $\begin{array}{l}b=6\text{ in}\text{.}\\ t=0.5\text{ in}\text{.}\\ h=12\text{ in}\text{.}\\ h_1=10.5\text{ in}\text{.}\end{array}$

Concept Used:

Following formula will be used

Minimum shear stress, $\tau =\frac{VQ}{Ib}$ .

Calculation:

Area of upper and lower flanges:

$A_1=b\left(\frac{h}{2}-\frac{h_1}{2}\right)=A_3$

Total area of cross section:

  $\begin{array}{l}A=A_1+A_3+t\times h_1\\ A=2b\left(\frac{h}{2}-\frac{h_1}{2}\right)+t\times h_1\\ A=b(h-h_1)+t\times h_1\\ A=6(12-10.5)+0.5\times 10.5=14.25{\text{ in}}^{\text{2}}\end{array}$

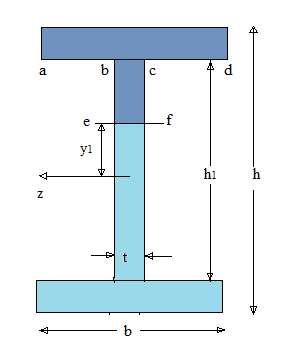
Second rectangle is $efcb$

  $A_2=t\left(\frac{h_1}{2}-y_1\right)$

In which $y_1$ is the distance from neutral axis to line $ef$

The first moment of areas of $A_1\text{ and }{A}_2$ about the neutral axis:

  $Q=A_1\left(\frac{h_1}{2}+\frac{h/2-h_1/2}{2}\right)+A_2\left(y_1+\frac{h_1/2-y_1}{2}\right)$

By putting the values of $A_1\text{ and }{A}_2$ , we get:

$\begin{array}{l}Q=\frac{b}{8}\left(h^2-h_1{}^2\right)+\frac{t}{8}\left(h_1{}^2-4y_1{}^2\right)\\ \text{So},\\ \tau =\frac{VQ}{It}=\frac{V}{It}\left[\frac{b}{8}\left(h^2-h_1{}^2\right)+\frac{t}{8}\left(h_1{}^2-4y_1{}^2\right)\right]\mathrm{...}\text{(1)}\end{array}$

The moment of inertia for the I section is given by following formula:

  $\begin{array}{l}I=\frac{b{h}^3}{12}-\frac{b{h}_1{}^3}{12}+\frac{t{h}_1{}^3}{12}\text{ about the neutral z axis}\text{.}\\ I=\frac{6\times {12}^3}{12}-\frac{6\times {10.5}^3}{12}+\frac{0.5\times {10.5}^3}{12}\\ I=333.422{\text{ in}}^{\text{4}}\end{array}$

The minimum value of shear stress will be at $\begin{array}{l}\\ cb,\end{array}$ when $\begin{array}{l}\\ y_1=\frac{h_1}{2}.\end{array}$

  $\begin{array}{l}{\tau }_{\min }=\frac{VQ}{It}=\frac{V}{It}\left[\frac{b}{8}\left(h^2-h_1{}^2\right)+\frac{t}{8}\left(h_1{}^2-4y_1{}^2\right)\right]\mathrm{...}\text{(1)}\\ {\tau }_{\min }=\frac{30}{333.422\times 0.5}\left[\frac{6}{8}\left({12}^2-{10.5}^2\right)+\frac{0.5}{8}\left({10.5}^2-4\times {(\frac{10.5}{2})}^2\right)\right]\\ {\tau }_{\min }=4.555\text{ ksi}\end{array}$

Conclusion:

The minimum shear stress in the web is $.{\tau }_{\min }=4.555\text{ ksi}$ .

To determine

To Find:

The average shear stress in web.

Answer to Problem 5.10.1P

The average shear stress in the web is = ${\tau }_{average}=5.7143\text{ ksi}$ and $Ratio=\frac{{\tau }_{\max }}{{\tau }_{average}}=1.014122$ .

Explanation of Solution

Given Information:

Shear Force $V=30\text{ k}$

Dimensions,

  $\begin{array}{l}b=6\text{ in}\text{.}\\ t=0.5\text{ in}\text{.}\\ h=12\text{ in}\text{.}\\ h_1=10.5\text{ in}\text{.}\end{array}$

Concept Used:

Following formula will be used

Average shear stress, ${\tau }_{average}=\frac{V}{t\times h_1}$ .

Calculation:

The average shear stress in the web is:

  $\begin{array}{l}{\tau }_{average}=\frac{V}{t\times h_1}\\ {\tau }_{average}=\frac{30}{0.5\times 10.5}\\ {\tau }_{average}=5.7143\text{ ksi}\\ \\ Ratio=\frac{{\tau }_{\max }}{{\tau }_{average}}=\frac{5.795}{5.7143}=1.014122\end{array}$

Conclusion:

The average shear stress in the web is = ${\tau }_{average}=5.7143\text{ ksi}$ and $Ratio=\frac{{\tau }_{\max }}{{\tau }_{average}}=1.014122$ .

To determine

To Find:

Shear force $V_{web}$ carried by web.

Answer to Problem 5.10.1P

The shear force in the web is = $V_{web}=28.254\text{k}$ and $Ratio=\frac{V_{web}}{V}=0.9418$ .

Explanation of Solution

Given Information:

Shear Force $V=30\text{ k}$

Dimensions,

  $\begin{array}{l}b=6\text{ in}\text{.}\\ t=0.5\text{ in}\text{.}\\ h=12\text{ in}\text{.}\\ h_1=10.5\text{ in}\text{.}\end{array}$

Concept Used:

Following formula will be used:

Shear stress in the web, $V_{web}=\frac{t{h}_1}{3}(2{\tau }_{\max }+{\tau }_{\min })$ .

Calculation:

Shear stress in the web:

  $\begin{array}{l}{V}_{web}=\frac{t{h}_1}{3}(2{\tau }_{\max }+{\tau }_{\min })\\ V_{web}=\frac{0.5\times 10.5}{3}(2\times 5.795+4.555)\\ V_{web}=28.254\text{k}\\ \\ Ratio=\frac{V_{web}}{V}=\frac{28.254}{30}=0.9418\end{array}$ .

Conclusion:

The shear force in the web is $.V_{web}=28.254\text{k}$ and $Ratio=\frac{V_{web}}{V}=0.9418$ .