Fundamentals of Physics Extended
10th Edition
ISBN: 9781118230725
Author: David Halliday, Robert Resnick, Jearl Walker
Publisher: Wiley, John & Sons, Incorporated
expand_more
expand_more
format_list_bulleted
Concept explainers
Videos
Textbook Question
Chapter 22, Problem 6Q
In Fig. 22-27, two identical circular nonconducting rings are centered on the same line with their planes perpendicular to the line. Each ring has charge that is uniformly distributed along its circumference. The rings each produce electric fields at points along the line. For three situations, the charges on rings A and B are, respectively, (1) q0 and q0, (2) −q0 and −q0, and (3) −q0 and q0. Rank the situations according to the magnitude of the net electric field at (a) point P1 midway between the rings, (b) point P2 at the center of ring B, and (c) point P3 to the right of ring B, greatest first.
Figure 22-27 Question 6.
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
In deep space two spheres each of radius 5.00 m are connected by a 3.00 × 102 m nonconducting cord. If a uniformly distributed charge of 35.0 μC resides on the surface of each sphere, calculate the tension in the cord.
Suppose a capacitor consists of two coaxial thin cylindrical conductors. The inner cylinder of radius ra has a charge of +Q, while the outer cylinder of radius rb has charge -Q. The electric field E at a radial distance r from the central axis is given by the function:
E = αe-r/a0 + β/r + b0
Suppose a capacitor consists of two coaxial thin cylindrical conductors. The inner cylinder of radius ra has a charge of +Q, while the outer cylinder of radius rb has charge -Q. The electric field E at a radial distance r from the central axis is given by the function: E = αe-r/a0 + β/r + b0
Chapter 22 Solutions
Fundamentals of Physics Extended
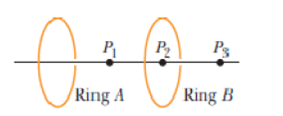
Ch. 22 - Figure 22-22 shows three arrangements of electric...Ch. 22 - Figure 22-23 shows two square arrays of charged...Ch. 22 - In Fig. 22-24, two particles of charge q are...Ch. 22 - Figure 22-25 shows four situations in which four...Ch. 22 - Figure 22-26 shows two charged particles fixed in...Ch. 22 - In Fig. 22-27, two identical circular...Ch. 22 - The potential energies associated with four...Ch. 22 - a In Checkpoint 4, if the dipole rotates from...Ch. 22 - Figure 22-28 shows two disks and a flat ring, each...Ch. 22 - In Fig. 22-29, an electron e travels through a...
Ch. 22 - In Fig. 22-30a, a circular plastic rod with...Ch. 22 - When three electric dipoles ire near each other,...Ch. 22 - Figure 22-32 shows three rods, each with the same...Ch. 22 - Figure 22-33 shows five protons that are launched...Ch. 22 - Sketch qualitatively the electric field lines both...Ch. 22 - In Fig. 22-34 the electric field lines on the left...Ch. 22 - SSM The nucleus of a plutonium-239 atom contains...Ch. 22 - Two charged particles are attached to an x axis:...Ch. 22 - SSM A charged particle produces an electric Held...Ch. 22 - What is the magnitude of a point charge that would...Ch. 22 - SSM ILW WWW In Fig. 22-35, the four particles form...Ch. 22 - GO In Fig. 22-36, the four particles are fixed in...Ch. 22 - GO Figure 22-37 shows two charged particles on an...Ch. 22 - GO Figure 22-38a shows two charged particles fixed...Ch. 22 - SSM Two charged particles are fixed to x axis:...Ch. 22 - GO Figure 22-39 shows an uneven arrangement of...Ch. 22 - GO Figure 22-40 shows a proton on the central...Ch. 22 - In Fig. 22-41, particle 1 of charge q1 = 5.00q and...Ch. 22 - In Fig. 22-42, the three particles are fixed in...Ch. 22 - Figure 22-43 shows a plastic ring of radius R =...Ch. 22 - Two charged beads are on the plastic ring in Fig....Ch. 22 - The electric field of an electric dipole along the...Ch. 22 - Figure 22-45 shows an electric dipole. What are...Ch. 22 - Equations 22-8 and 22-9 are approximations of the...Ch. 22 - SSM Electric quadrupole. Figure 22-46 shows a...Ch. 22 - Density, density, density. a A charge 300e is...Ch. 22 - Figure 22-47 shows two parallel nonconducting...Ch. 22 - A thin nonconducting rod with a uniform...Ch. 22 - Figure 22-49 shows three circular arcs centered on...Ch. 22 - GO ILW In Fig. 22-50, a thin glass rod forms a...Ch. 22 - GO In Fig, 22-51, two curved plastic rods, one of...Ch. 22 - Charge is uniformly distributed around a ring of...Ch. 22 - GO Figure 22-52a shows a nonconducting rod with a...Ch. 22 - GO Figure 22-53 shows two concentric rings, of...Ch. 22 - SSM ILW WWW In Fig. 22-54, a nonconducting rod of...Ch. 22 - GO In Fig. 22-55, positive charge q = 7.81 pC is...Ch. 22 - GO In Fig. 22-56, a semi-infinite nonconducting...Ch. 22 - A disk of radius 2.5 cm has a surface charge...Ch. 22 - SSM WWW At what distance along the central...Ch. 22 - A circular plastic disk with radius R = 2.00 cm...Ch. 22 - Suppose you design an apparatus in which a...Ch. 22 - Figure 22-58a shows a circular disk that is...Ch. 22 - In Millikans experiment, an oil drop of radius...Ch. 22 - GO An electron with a speed of 5.00 108 cm/s...Ch. 22 - SSM A charged cloud system produces an electric...Ch. 22 - Humid air breaks down its molecules become ionized...Ch. 22 - SSM An electron is released from rest in a uniform...Ch. 22 - An alpha particle the nucleus of a helium atom has...Ch. 22 - ILW An electron on the axis of an electric dipole...Ch. 22 - An electron is accelerated eastward at 1.80 ...Ch. 22 - SSM Beams of high-speed protons can be produced in...Ch. 22 - In Fig. 22-59, an electron e is to be released...Ch. 22 - A 10.0 g block with a charge of 8.00 10-5 C is...Ch. 22 - At some instant the velocity components of an...Ch. 22 - Assume that a honeybee is a sphere of diameter...Ch. 22 - An electron eaters a region of uniform electric...Ch. 22 - GO Two large parallel copper plates are 5.0 cm...Ch. 22 - GO In Fig. 22-61, an electron is shot at an...Ch. 22 - ILW A uniform electric field exists in a region...Ch. 22 - An electric dipole consists of charges 2e and -2e...Ch. 22 - SSM An electric dipole consisting of charges of...Ch. 22 - A certain electric dipole is placed in a uniform...Ch. 22 - How much work is required to turn an electric...Ch. 22 - A certain electric dipole is placed in a uniform...Ch. 22 - Find an expression for the oscillation frequency...Ch. 22 - a What is the magnitude of an electrons...Ch. 22 - A spherical water drop 1.20 m in diameter is...Ch. 22 - Three particles, each with positive charge Q, form...Ch. 22 - In Fig. 22-64a, a particle of charge Q produces an...Ch. 22 - A proton and an electron form two comers of an...Ch. 22 - A charge uniform linear density = 9.0 nC/m lies on...Ch. 22 - In Fig. 22-65, eight particles form a square in...Ch. 22 - Two particles, each with a charge of magnitude 12...Ch. 22 - The following table gives the charge seen by...Ch. 22 - A charge of 20 nC is uniformly distributed along a...Ch. 22 - An electron is constrained to the central axis of...Ch. 22 - SSM The electric field in an xy plane produced by...Ch. 22 - a What total excess charge q must the disk in Fig....Ch. 22 - In Fig. 22-66, particle 1 of charge 1.00 C,...Ch. 22 - In Fig. 22-67, an electric dipole swings from an...Ch. 22 - A particle of charge q1 is at the origin of an x...Ch. 22 - Two particles, each of positive charge q, are...Ch. 22 - A clock face has negative point charges q, 2q,...Ch. 22 - Calculate the electric dipole moment of an...Ch. 22 - An electric field E with an average magnitude of...Ch. 22 - A circular rod has a radius of curvature R = 9.00...Ch. 22 - SSM An electric dipole with dipole moment p= 3.00 ...Ch. 22 - In Fig. 22-68, a uniform, upward electric field E...Ch. 22 - For the data of Problem 70, assume that the charge...Ch. 22 - In Fig. 22-66, particle 1 of charge 2.00 pC,...Ch. 22 - In Fig. 22-69, particle 1 of charge q1 = 1.00pC...
Additional Science Textbook Solutions
Find more solutions based on key concepts
3.1 The reaction between reactant A (blue spheres) and reactant B (red spheres) is shown in the
following diag...
Chemistry: The Central Science (14th Edition)
Determine [OH], [H+], and the pH of each of the following solutions. a. 1.0 M KCl b. 1.0 M KC2H3O2
Chemistry
WHAT IF? You are studying nitrogen cycling on the Serengeti Plain in Africa. During your experiment, a herd of ...
Campbell Biology in Focus (2nd Edition)
Why is an endospore called a resting structure? Of what advantage is an endospore to a bacterial cell?
Microbiology: An Introduction
Which type of cartilage is most plentiful in the adult body?
Anatomy & Physiology (6th Edition)
Draw the enol tautomers for each of the following compounds. For compounds that have more than one enol tautome...
Organic Chemistry (8th Edition)
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, physics and related others by exploring similar questions and additional content below.Similar questions
- Two solid spheres, both of radius 5 cm, carry identical total charges of 2 C. Sphere A is a good conductor. Sphere B is an insulator, and its charge is distributed uniformly throughout its volume. (i) How do the magnitudes of the electric fields they separately create at a radial distance of 6 cm compare? (a) EA EB = 0 (b) EA EB 0 (c) EA = EB 0 (d) 0 EA EB (e) 0 = EA EB (ii) How do the magnitudes of the electric fields they separately create at radius 4 cm compare? Choose from the same possibilities as in part (i).arrow_forwardA circular ring of charge with radius b has total charge q uniformly distributed around it. What is the magnitude of the electric field at the center of the ring? (a) 0 (b) keq/b2 (c) keq2/b2 (d) keq2/b (e) none of those answersarrow_forwardaA plastic rod of length = 24.0 cm is uniformly charged with a total charge of +12.0 C. The rod is formed into a semicircle with its center at the origin of the xy plane (Fig. P24.34). What are the magnitude and direction of the electric field at the origin? Figure P24.34arrow_forward
- Two large insulating parallel plates carry positive charge of equal magnitude that is distributed uniformly over their inner surfaces. Rank the points 1 through 5 according to the magnitude of the electric field at the points, least to greatest.arrow_forwardWe consider a conducting sphere of radius a = 1m in a uniform electric field E0= 1000 V/m. A uniform field can be thought of as being produced by appropriate positive and negative charges at infinity. Φ = Q/4TTEO (r2R2+2rR cos 0) 1/2 (2² + R2 aQ/4TE0 Q/4 TTED 2rR cos 0)1/2 aQ/4π€0 1/2 1/2 a¹ 2a²r a² 2a²r + COS R2 COS R² R R² R 1 Απευ 20 R² 2Q r cos 0 + 2 a² cos A +... (2.12) (2.13) where the omitted terms vanish in the limit R. In that limit 20/4πTEOR² becomes the applied uniform field, so that the potential is Φ --E (1-5) cos 0 (2.14) 1) Give the derivation process of eq (2.12) 2) Plot the distributions of the potential and current density vector. 3) Compare the results from eq(2.12) and eq(2.14) as R varies.arrow_forwardThree charges, q1 = 1 µC, q2 = 2 µC and q3 = 3 µC are placed in a line with 20 cm between %3D each of them. So qat a = 0, q2 at z = 20 cm and q3 at z = 40 cm. Calculate the energy stored in the collection of charges. (a) -0.62 J (b) -0.43 J (c) +0.43 J (d) +0.62 Jarrow_forward
- Two conducting spheres are far apart. The smaller sphere of radius R carries a total charge Q. The larger sphere is neutral and has a radius r where r =4.5 R. After the two spheres are connected by a conducting wire, the charges on the larger and smaller, respectively, are:arrow_forwardA cylindrical distribution of charge ρ = α /√ r where α = 2 µC/m 5/2 extends from 0 cm to 9.3 cm . Concentric with this is a dielectric shell with 5.44 of inner radius 16.6 cm and outer radius 24.9 cm . What is the electric field at 3.53 cm ?arrow_forward3 1 00 H X). Shown in the figure are two arcs of charge centered at the origin. The inner arc has a radius of curvature of 0.2 meters and a linear charge density of -50 C/m. The outer arc has a radius of curvature of 0.6 meters and a linear charge density of 80 μC/m. With theta given as 30 degrees, calculate the work it would take to bring a 60 μC point charge from infinity to the origin. Enter your answer in units of joules rounding your final answer to two decimal places. If the work is negative, a negative value must be entered. OLDE OAarrow_forward
- A non-conducting sphere of radius R = 7.0 cm carries a charge Q = 4.0 mC distributed uniformly throughout its volume. At what distance, measured from the center of the sphere, does the electric field reach a value equal to half its maximum value?arrow_forwardThree point charges at q1 x = 0, q2 at x = 5 cm, and q3 at x = 3 cm. Find the ratio of q1:q2 if q3 is at equilibriumarrow_forward(a) Red blood cells often become charged and can be treated as point charges. Healthy red blood cells are negatively charged, but unhealthy cells (due to the presence of a bacteria, for example) can become positively charged. In the figure, three red blood cells are oriented such that they are located on the corners of an equilateral triangle. The red blood cell charges are A = 2.20 pC, B = 7.50 pC, and C = −4.40 pC. Given these charges, what would the magnitude and direction of the electric field be at cell A? (1 pC = 1 ✕ 10−12 C.) magnitude directionarrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning
Principles of Physics: A Calculus-Based Text
Physics
ISBN:9781133104261
Author:Raymond A. Serway, John W. Jewett
Publisher:Cengage Learning
Physics for Scientists and Engineers: Foundations...
Physics
ISBN:9781133939146
Author:Katz, Debora M.
Publisher:Cengage Learning
Electric Fields: Crash Course Physics #26; Author: CrashCourse;https://www.youtube.com/watch?v=mdulzEfQXDE;License: Standard YouTube License, CC-BY