Chapter 21, Problem 53A

a.

To determine

To sketch: Electric field lines between two like charges of equal magnitude.

Explanation of Solution

Introduction:

Electric field lines:

The electric field lines are actually the line of force. They are imaginary in nature. To determine the direction of net field at any point, a tangent is drawn at that point.

The lines of electric field originate from the positive charge and terminates in the negative charge.

The electric field lines between two like charges of equal magnitude is shown below,

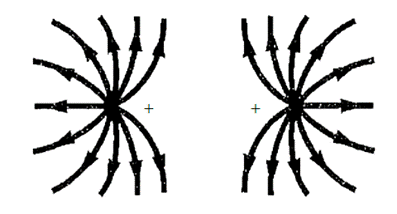
The lines of electric field are always perpendicular to the surface of the charge. Since the two charge are similar in nature and magnitude, so they will repel each other and hence the lines of electric field points away from the positive charge as shown above.

The lines of electric field are assumed to terminates at infinity.

b.

To determine

To sketch: Electric field lines between two unlike charges of equal magnitude.

Explanation of Solution

Introduction:

Electric field lines:

The electric field lines are actually the line of force. They are imaginary in nature. To determine the direction of net field at any point, a tangent is drawn at that point.

The lines of electric field originate from the positive charge and terminates in the negative charge.

The electric field lines between two unlike charges that is a positive and negative charge is shown below,

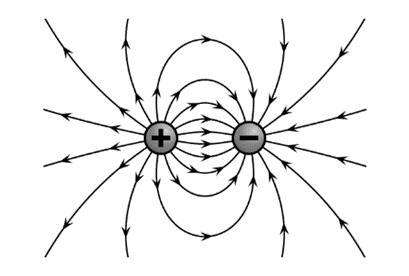
The lines of electric field are always perpendicular to the surface of the charge. Since the two charge are similar in magnitude but different in nature, so the lines of electric field originate from positive and terminate at negative charge as shown above.

c.

To determine

To sketch: Electric field lines between a positive charge and a negative charge of double magnitude.

Explanation of Solution

Introduction:

Electric field lines:

The electric field lines are actually the line of force. They are imaginary in nature. To determine the direction of net field at any point, a tangent is drawn at that point.

The lines of electric field originate from the positive charge and terminates in the negative charge.

The electric field lines between a positive and negative charge of double magnitude is shown below,

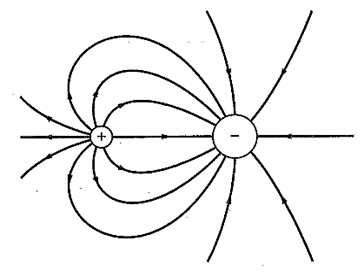
The lines of electric field are always perpendicular to the surface of the charge. Since the two charge differ in magnitude as well as nature, so the lines of electric field originate from positive and terminate at negative charge as shown above. As the negative charge is double in magnitude, so its electric field is high which is represented by more field lines.

d.

To determine

To sketch: Electric field lines between two oppositely charged parallel plates.

Explanation of Solution

Introduction:

Electric field lines:

The electric field lines are actually the line of force. They are imaginary in nature. To determine the direction of net field at any point, a tangent is drawn at that point.

The lines of electric field originate from the positive charge and terminates in the negative charge.

The electric field lines between two oppositely charged parallel plates is shown below,

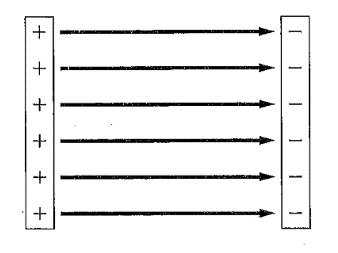
The lines of electric field are always perpendicular to the surface of the charge. Here, the lines of electric field originate from positive and terminate at negative charge as shown above.