Fundamentals of Physics Extended
10th Edition
ISBN: 9781118230725
Author: David Halliday, Robert Resnick, Jearl Walker
Publisher: Wiley, John & Sons, Incorporated
expand_more
expand_more
format_list_bulleted
Videos
Textbook Question
Chapter 20, Problem 32P
GO A Carnot engine is set up to produce a certain work W per cycle. In each cycle, energy in the form of heat QH is transferred to the working substance of the engine from the higher-temperature thermal reservoir, which is at an adjustable temperature TH. The lower-temperature thermal reservoir is maintained at temperature TL = 250 K. Figure 20-28 gives QH for a range of TH. The scale of the vertical axis is set by QHs = 6.0 kJ. If TH is set at 550 K, what is QH?
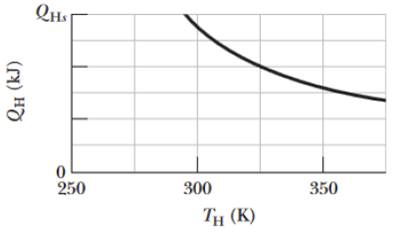
Figure 20-28 Problem 32.
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
53. ssm A Carnot engine has an efficiency of 0.700, and the temperature
of its cold reservoir is 378 K. (a) Determine the temperature of its hot res-
ervoir. (b) If 5230 J of heat is rejected to the cold reservoir, what amount
of heat is put into the engine?
32 A Carnot engine is set up to produce a certain work W
per cycle. In each cycle, energy in the form of heat QH is
transferred to the working substance of the engine from
the higher-temperature thermal reservoir, which is at an adjustable
temperature T. The lower-temperature thermal reservoir is main-
tained at temperature T = 250 K. Figure 20-28 gives QH for a
range of TH. The scale of the vertical axis is set by QH. = 6.0 kJ. If
TH is set at 550 K, what is Qu?
%3D
QH-
250
300
350
Figure 20-28 Problem 32.
TH (K)
Qu (kJ)
A piston–cylinder device contains air that undergoes a reversible thermodynamic cycle. Initially, air is at 400 kPa and 300 K with a volume of 0.3 m3 air is first expanded isothermally to 150 kPa, then compressed adiabatically to the initial pressure, and finally compressed at the constant pressure to the initial state. Accounting for the variation of specific heats with temperature, determine the work and heat transfer for each process.
Chapter 20 Solutions
Fundamentals of Physics Extended
Ch. 20 - Point i in Fig. 20-19 represents the initial state...Ch. 20 - In lour experiments, blocks A and B, starting ill...Ch. 20 - A gas, confined to an insulated cylinder, is...Ch. 20 - An ideal monatomic gas at initial temperature T0...Ch. 20 - In four experiments, 2.5 mol of hydrogen gas...Ch. 20 - A box contains 100 atoms in a configuration that...Ch. 20 - Does the entropy per cycle increase, decrease, or...Ch. 20 - Three Carnot engines operate between temperature...Ch. 20 - An inventor claims to have invented four engines,...Ch. 20 - Does the entropy per cycle increase, decrease, or...
Ch. 20 - SSM Suppose 4.00 mol of an ideal gas undergoes a...Ch. 20 - An ideal gas undergoes a reversible isothermal...Ch. 20 - ILW A 2.50 mol sample of an ideal gas expands...Ch. 20 - How much energy must be transferred as heat for a...Ch. 20 - ILW Find a the energy absorbed as heat and b the...Ch. 20 - a What is the entropy change of a 12.0 g ice cube...Ch. 20 - ILW A 50.0 g block of copper whose temperature is...Ch. 20 - At very low temperatures, the molar specific heat...Ch. 20 - A 10 g ice cube at 10oC is placed in a lake whose...Ch. 20 - A 364 g block is put in contact with a thermal...Ch. 20 - SSM WWW In an experiment, 200 g of aluminum with a...Ch. 20 - A gas sample undergoes a reversible isothermal...Ch. 20 - In the irreversible process of Fig. 20-5, let the...Ch. 20 - Prob. 14PCh. 20 - A mixture of 1773 g of water and 227 g of ice is...Ch. 20 - GO An 8.0 g ice cube at -10C is put into a Thermos...Ch. 20 - Prob. 17PCh. 20 - GO A 2.0 mol sample of an ideal monatomic gas...Ch. 20 - Suppose 1.00 mol of a monatomic ideal gas is taken...Ch. 20 - Expand 1.00 mol of an monatomic gas initially at...Ch. 20 - GO Energy can be removed from water as heat at and...Ch. 20 - GO An insulated Thermos contains 130 g of water at...Ch. 20 - A Carnot engine whose low-temperature reservoir is...Ch. 20 - A Carnot engine absorbs 52 kJ as heat and exhausts...Ch. 20 - A Carnot engine has an efficiency of 22.0. It...Ch. 20 - In a hypothetical nuclear fusion reactor, the fuel...Ch. 20 - SSM WWW A Carnot engine operates between 235C and...Ch. 20 - In the first stage of a two-stage Carnot engine,...Ch. 20 - GO Figure 20-27 shows a reversible cycle through...Ch. 20 - A 500 W Carnot engine operates between...Ch. 20 - The efficiency of a particular car engine is 25...Ch. 20 - GO A Carnot engine is set up to produce a certain...Ch. 20 - SSM ILW Figure 20-29 shows a reversible cycle...Ch. 20 - GO An ideal gas 1.0 mol is the working substance...Ch. 20 - The cycle in Fig. 20-31 represents the operation...Ch. 20 - How much work must be done by a Carnot...Ch. 20 - SSM A heat pump is used to heal a building, The...Ch. 20 - The electric motor of a heat pump transfers energy...Ch. 20 - SSM A Carnot air conditioner lakes energy from the...Ch. 20 - To make ice, a freezer that is a reverse Carnot...Ch. 20 - ILW An air conditioner operating between 93F and...Ch. 20 - The motor in a refrigerator has a power of 200 W....Ch. 20 - GO Figure 20-32 represents a Carnot engine that...Ch. 20 - a During each cycle, a Carnot engine absorbs 750 J...Ch. 20 - Prob. 45PCh. 20 - A box contains N identical gas molecules equally...Ch. 20 - SSM WWW A box contains N gas molecules, Consider...Ch. 20 - Four particles are in the insulated box of Fig....Ch. 20 - A cylindrical copper rod of length 1.50 m and...Ch. 20 - Suppose 0.550 mol of an ideal gas is isothermally...Ch. 20 - Prob. 51PCh. 20 - Suppose 1.0 mol of a monatomic ideal gas initially...Ch. 20 - GO Suppose that a deep shaft were drilled in...Ch. 20 - What is the entropy change for 3.20 mol of an...Ch. 20 - A 600 g lump of copper at 80.0C is placed in 70.0...Ch. 20 - Figure 20-33 gives the force magnitude F versus...Ch. 20 - The temperature of 1.00 mol of a monatomic ideal...Ch. 20 - Repeat Problem 57, with the pressure now kept...Ch. 20 - SSM A 0.600 kg sample of water is initially ice at...Ch. 20 - A three-step cycle is undergone by 3.4 mol of an...Ch. 20 - An inventor has built an engine X and claims that...Ch. 20 - Suppose 2.00 mol of a diatomic gas is taken...Ch. 20 - A three-step cycle is undergone reversibly by 4.00...Ch. 20 - a A Carnot engine operates between a hot reservoir...Ch. 20 - A 2.00 mol diatomic gas initially at 300 K...Ch. 20 - An ideal refrigerator does 150 J of work to remove...Ch. 20 - Suppose that 260 J is conducted from a...Ch. 20 - An apparatus that liquefies helium is in a room...Ch. 20 - GO A brass rod is in thermal contact with a...Ch. 20 - A 45.0 g block of tungsten at 30.0C and a 25.0 g...Ch. 20 - Prob. 71PCh. 20 - Calculate the efficiency of a fossil-fuel power...Ch. 20 - SSM A Carnot refrigerator extracts 35.0 kJ as heat...Ch. 20 - A Carnot engine whose high-temperature reservoir...Ch. 20 - SSM System A of three particles and system B of...Ch. 20 - Figure 20-36 shows a Carnot cycle on a T-S...Ch. 20 - Find the relation between the efficiency of a...Ch. 20 - A Carnot engine has a power of 500 W. It operates...Ch. 20 - In a real refrigerator, the low-temperature coils...
Additional Science Textbook Solutions
Find more solutions based on key concepts
Why can algae and cyanobacteria be considered indicators of productivity as well as of pollution?
Laboratory Experiments in Microbiology (12th Edition) (What's New in Microbiology)
Match the following examples of mutagens. Column A Column B ___a. A mutagen that is incorporated into DNA in pl...
Microbiology: An Introduction
Determine [OH], [H+], and the pH of each of the following solutions. a. 1.0 M KCl b. 1.0 M KC2H3O2
Chemistry
33. Classify each statement as an observation, a law, or a theory.
a. All matter is made up of tiny, indestruc...
Chemistry: A Molecular Approach (4th Edition)
2 Of the uterus, small intestine, spinal cord, and heart, which is/are in the dorsal body cavity?
Anatomy & Physiology (6th Edition)
Name the components (including muscles) of the thoracic cage. List the contents of the thorax.
Human Physiology: An Integrated Approach (8th Edition)
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, physics and related others by exploring similar questions and additional content below.Similar questions
- The energy input to an engine is 3.00 times greater than the work it performs. (i) What is its thermal efficiency? (a) 3.00 (b) 1.00 (c) 0.333 (d) impossible to determine (ii) What fraction of the energy input is expelled to the cold reservoir? (a) 0.333 (b) 0.667 (c) 1.00 (d) impossible to determinearrow_forwardA multicylinder gasoline engine in an airplane, operating at 2.50 103 rev/min, takes in energy 7.89 103 J and exhausts 4.58 103 J for each revolution of the crankshaft. (a) How many liters of fuel does it consume in 1.00 h of operation if the heat of combustion of the fuel is equal to 4.03 107 J/L? (b) What is the mechanical power output of the engine? Ignore friction and express the answer in horsepower. (c) What is the torque exerted by the crankshaft on the load? (d) What power must the exhaust and cooling system transfer out of the engine?arrow_forwardA copper rod of cross-sectional area 5.0 cm2 and length 5.0 m conducts heat from a heat reservoir at 373 K to one at 273 K. What is the time rate of change of the universe's entropy for this process?arrow_forward
- A Carnot engine employs 1.5 mol of nitrogen gas as a working substance, which is considered as an ideal diatomic gas with =7.5 at the working temperatures of the engine. The Carnot cycle goes in the cycle ABCDA with AB being an isothermal expansion. The volume at points A and C of the cycle are 5.0103 m3 and 0.15 L, respectively. The engine operates between two thermal baths of temperature 500 K 300 K. (a) Find the values of volume at B and D. (b) How much heat is absorbed by the gas in the AB isothermal expansion? (c) How much work is done by the gas in the AB isothermal expansion? (d) How much heat is given up by the gas in the CD isothermal expansion? (e) How much work is done by the gas in the CD isothermal compression? (f) How much work is done by the gas in the BC adiabatic expansion? (g) How much work is done by the gas in the DA adiabatic compression? (h) Find the value of efficiency of the engine based on the net and heat input. Compare this value to the efficiency of a Carnot engine based on the temperatures of the baths.arrow_forwardTwo moles of nitrogen gas, with =7/5 for ideal diatomic gases, occupies a volume of 102 m3 in an insulated cylinder at temperature 300 K. The gas is adiabatically and reversibly compressed to a volume of 5 L. The piston of the cylinder is locked in its place, and the insulation around the cylinder is removed. The heat-conducting cylinder is then placed in a 300-K bath. Heat from the compressed gas leaves the gas, and the temperature of the gas becomes 300 K again. The gas is then slowly expanded at the fixed temperature 300 K until the volume of the gas becomes 102 m3, thus making a complete cycle for the gas. For the entire cycle, calculate (a) the work done by the gas, (b) the heat into or out of the gas, (c) the change in the internal energy of the gas, and (d) the change in entropy of the gas.arrow_forwardAn amount of n moles of a monatomic ideal gas in a conducting container with a movable piston is placed in a large thermal heat bath at temperature T1 and the gas is allowed to come to equilibrium. After the equilibrium is leached, the pressure on the piston is lowered so that the gas expands at constant temperature. The process is continued quasi-statically until the final pressure is 4/3 of the initial pressure p1 . (a) Find the change in the internal energy of the gas. (b) Find the work done by the gas. (c) Find the heat exchanged by the gas, and indicate, whether the gas takes in or gives up heat.arrow_forward
- An ideal gas with specific heat ratio confined to a cylinder is put through a closed cycle. Initially, the gas is at Pi, Vi, and Ti. First, its pressure is tripled under constant volume. It then expands adiabatically to its original pressure and finally is compressed isobarically to its original volume. (a) Draw a PV diagram of this cycle. (b) Determine the volume at the end of the adiabatic expansion. Find (c) the temperature of the gas at the start of the adiabatic expansion and (d) the temperature at the end of the cycle. (e) What was the net work done on the gas for this cycle?arrow_forwardThe insulated cylinder shown below is closed at both ends and contains an insulating piston that is flee to move on frictionless bearings. The piston divides the chamber into two compartments containing gases A and B. Originally, each compartment has a volume of 5.0102 m3 and contains a monatomic ideal gas at a temperature of and a pressure of 1.0 atm. (a) How many moles of gas are in each compartment? (b) Heat Q is slowly added to A so that it expands and B is compressed until the pressure of both gases is 3.0 atm. Use the fact that the compression of B is adiabatic to determine the final volume of both gases. (c) What are their final temperatures? (d) What is the value of Q?arrow_forwardTwo moles of a monatomic ideal gas such as oxygen is compressed adiabatically and reversibly from a state (3 atm, 5 L) to a state with a pressure of 4 atm. (a) Find the volume and temperature of the final state. (b) Find the temperature of the initial state. (c) Find work done by the gas in the process. (d) Find the change in internal energy in the process. Assume Cv=5R and Cp=Cv+R for the diatomic ideal gas in the conditions given.arrow_forward
- Two moles of an ideal gas with the heat capacity per mole Cp=7R/2 at constant pressure go through the cycle acb shown below. You are given the temperatures at those three points as Ta, Tb and Tc, respectively. Process cb is adiabatic. (i) What is the heat transferred to the gas during ac process? (ii) Calculate the total work for the whole cycle using the given parameters only. (R: gas constant) P b a Varrow_forwarda) A Carnot heat engine receives heat from a reservoir at 700°C at a rate of 600 kJ/min and rejects the waste heat to the ambient air at 25°C. The entire work output of the heat engine is used to drive a refrigerator that removes heat from the refrigerated space at - 6°C and transfers it to the same ambient air at 25°C. Determine (a) the maximum rate of heat removal from the refrigerated space and (b) the total rate of heat rejection to the ambient air.arrow_forwardThe Sun radiates energy at the rate of 3.80×1026 W from its 5500C surface into dark empty space (a negligible fraction radiates onto Earth and the other planets). The effective temperature of deep space is -270C. (a) What is the increase in entropy in one day due to this heat transfer? (b) How much work is made unavailable?arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning
Physics for Scientists and Engineers, Technology ...PhysicsISBN:9781305116399Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Principles of Physics: A Calculus-Based Text
Physics
ISBN:9781133104261
Author:Raymond A. Serway, John W. Jewett
Publisher:Cengage Learning
Physics for Scientists and Engineers: Foundations...
Physics
ISBN:9781133939146
Author:Katz, Debora M.
Publisher:Cengage Learning
Physics for Scientists and Engineers, Technology ...
Physics
ISBN:9781305116399
Author:Raymond A. Serway, John W. Jewett
Publisher:Cengage Learning
The Second Law of Thermodynamics: Heat Flow, Entropy, and Microstates; Author: Professor Dave Explains;https://www.youtube.com/watch?v=MrwW4w2nAMc;License: Standard YouTube License, CC-BY