
GO Figure 20-27 shows a reversible cycle through which 1.00 mol of a monatomic ideal gas is taken. Assume that p = 2p0, V = 2V0, p0 = 1.01 × 105 Pa, and V0 = 0.0225 m3. Calculate (a) the work done during the cycle, (b) the energy added as heat during stroke abc, and (c) the efficiency of the cycle, (d) What is the efficiency of a Carnot engine operating between the highest and lowest temperatures that occur in the cycle? (e) Is this greater than or less than the efficiency calculated in (c)?
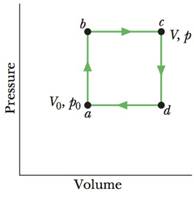
Figure 20-27 Problem 29.
Trending nowThis is a popular solution!

Chapter 20 Solutions
Fundamentals of Physics Extended
Additional Science Textbook Solutions
Chemistry: A Molecular Approach (4th Edition)
Laboratory Experiments in Microbiology (12th Edition) (What's New in Microbiology)
Living By Chemistry: First Edition Textbook
Chemistry (7th Edition)
Biology: Life on Earth with Physiology (11th Edition)
Chemistry & Chemical Reactivity
- RAD127 Radiographic Equipment and Computers SI Units in Radiography Ch. 1 & 2 Instructions: Provide the units for each of the following in full and short forms 1. Mass - kg, 9 or (1b)) ・ 2. Energy, Work - W = FD,J 3. Air kerma -(Gya) 4. Absorbed Dose- 5. Effective Dose J/kg (94+) jlkg J/kg, Sv 6. Radioactivity - 5-1, Bq 7. Weight 8. Time 9. Force 10. Power B9 wt, wt-mg, N -(s) F= ma, N, OR 1b. (JIS), P= work It = Fdlt, Jarrow_forwardanswer 1-8arrow_forward1 . Solve the equation 2/7=y/3 for y. 2. Solve the equation x/9=2/6 for x. 3. Solve the equation z + 4 = 10 This is algebra and the equation is fraction.arrow_forward
- two satellites are in circular orbits around the Earth. Satellite A is at an altitude equal to the Earth's radius, while satellite B is at an altitude equal to twice the Earth's radius. What is the ratio of their periods, Tb/Taarrow_forwardFresnel lens: You would like to design a 25 mm diameter blazed Fresnel zone plate with a first-order power of +1.5 diopters. What is the lithography requirement (resolution required) for making this lens that is designed for 550 nm? Express your answer in units of μm to one decimal point. Fresnel lens: What would the power of the first diffracted order of this lens be at wavelength of 400 nm? Express your answer in diopters to one decimal point. Eye: A person with myopic eyes has a far point of 15 cm. What power contact lenses does she need to correct her version to a standard far point at infinity? Give your answer in diopter to one decimal point.arrow_forwardParaxial design of a field flattener. Imagine your optical system has Petzal curvature of the field with radius p. In Module 1 of Course 1, a homework problem asked you to derive the paraxial focus shift along the axis when a slab of glass was inserted in a converging cone of rays. Find or re-derive that result, then use it to calculate the paraxial radius of curvature of a field flattener of refractive index n that will correct the observed Petzval. Assume that the side of the flattener facing the image plane is plano. What is the required radius of the plano-convex field flattener? (p written as rho )arrow_forward
- 3.37(a) Five free electrons exist in a three-dimensional infinite potential well with all three widths equal to \( a = 12 \, \text{Å} \). Determine the Fermi energy level at \( T = 0 \, \text{K} \). (b) Repeat part (a) for 13 electrons. Book: Semiconductor Physics and Devices 4th ed, NeamanChapter-3Please expert answer only. don't give gpt-generated answers, & please clear the concept of quantum states for determining nx, ny, nz to determine E, as I don't have much idea about that topic.arrow_forward3.37(a) Five free electrons exist in a three-dimensional infinite potential well with all three widths equal to \( a = 12 \, \text{Å} \). Determine the Fermi energy level at \( T = 0 \, \text{K} \). (b) Repeat part (a) for 13 electrons. Book: Semiconductor Physics and Devices 4th ed, NeamanChapter-3Please expert answer only. don't give gpt-generated answers, & please clear the concept of quantum states for determining nx, ny, nz to determine E, as I don't have much idea about that topic.arrow_forwardNo chatgpt pls will upvotearrow_forward
- Use the following information to answer the next question. Two mirrors meet an angle, a, of 105°. A ray of light is incident upon mirror A at an angle, i, of 42°. The ray of light reflects off mirror B and then enters water, as shown below: Incident ray at A Note: This diagram is not to scale. a Air (n = 1.00) Water (n = 1.34) 1) Determine the angle of refraction of the ray of light in the water. Barrow_forwardHi can u please solvearrow_forward6. Bending a lens in OpticStudio or OSLO. In either package, create a BK7 singlet lens of 10 mm semi-diameter and with 10 mm thickness. Set the wavelength to the (default) 0.55 microns and a single on-axis field point at infinite object distance. Set the image distance to 200 mm. Make the first surface the stop insure that the lens is fully filled (that is, that the entrance beam has a radius of 10 mm). Use the lens-maker's equation to calculate initial glass curvatures assuming you want a symmetric, bi-convex lens with an effective focal length of 200 mm. Get this working and examine the RMS spot size using the "Text" tab of the Spot Diagram analysis tab (OpticStudio) or the Spd command of the text widnow (OSLO). You should find the lens is far from diffraction limited, with a spot size of more than 100 microns. Now let's optimize this lens. In OpticStudio, create a default merit function optimizing on spot size.Then insert one extra line at the top of the merit function. Assign the…arrow_forward

 Physics for Scientists and Engineers, Technology ...PhysicsISBN:9781305116399Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers, Technology ...PhysicsISBN:9781305116399Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning
Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning College PhysicsPhysicsISBN:9781938168000Author:Paul Peter Urone, Roger HinrichsPublisher:OpenStax College
College PhysicsPhysicsISBN:9781938168000Author:Paul Peter Urone, Roger HinrichsPublisher:OpenStax College College PhysicsPhysicsISBN:9781305952300Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning
College PhysicsPhysicsISBN:9781305952300Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning





