
An inventor has built an engine X and claims that its efficiency εX is greater than the efficiency ε of an ideal engine operating between the same two temperatures. Suppose you couple engine X to an ideal refrigerator (Fig. 20-34a) and adjust the cycle of engine X so that the work per cycle it provides equals the work per cycle required by the ideal refrigerator. Treat this combination as a single unit and show that if the inventor’s claim were true (if εX>ε), the combined unit would act as a perfect refrigerator (Fig. 20-34b), transferring energy as heat from the low-temperature reservoir to the high-temperature reservoir without the need for work.
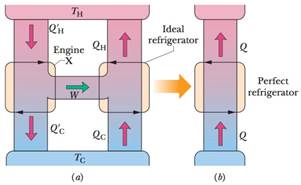
Figure 20-34 Problem 61
Want to see the full answer?
Check out a sample textbook solution
Chapter 20 Solutions
Fundamentals of Physics Extended
Additional Science Textbook Solutions
Introductory Chemistry (6th Edition)
College Physics: A Strategic Approach (3rd Edition)
Physics for Scientists and Engineers: A Strategic Approach, Vol. 1 (Chs 1-21) (4th Edition)
Anatomy & Physiology (6th Edition)
Human Physiology: An Integrated Approach (8th Edition)
Principles of Anatomy and Physiology
- Your RL circuit has a characteristic time constant of 19.5 ns, and a resistance of 4.60 MQ. (a) What is the inductance (in H) of the circuit? 0.00897 × H (b) What resistance (in MQ) should you use (instead of the 4.60 MQ resistor) to obtain a 1.00 ns time constant, perhaps needed for quick response in an oscilloscope? 8.97 * ΜΩarrow_forwardYour RL circuit has a characteristic time constant of 19.5 ns, and a resistance of 4.60 MQ. (a) What is the inductance (in H) of the circuit? H (b) What resistance (in MQ) should you use (instead of the 4.60 MQ resistor) to obtain a 1.00 ns time constant, perhaps needed for quick response in an oscilloscope? ΜΩarrow_forwardAt a distance of 0.212 cm from the center of a charged conducting sphere with radius 0.100cm, the electric field is 485 N/C . What is the electric field 0.598 cm from the center of the sphere? At a distance of 0.196 cmcm from the axis of a very long charged conducting cylinder with radius 0.100cm, the electric field is 485 N/C . What is the electric field 0.620 cm from the axis of the cylinder? At a distance of 0.202 cm from a large uniform sheet of charge, the electric field is 485 N/C . What is the electric field 1.21 cm from the sheet?arrow_forward
- A hollow, conducting sphere with an outer radius of 0.260 m and an inner radius of 0.200 m has a uniform surface charge density of +6.67 × 10−6 C/m2. A charge of -0.800 μC is now introduced into the cavity inside the sphere. What is the new charge density on the outside of the sphere? Calculate the strength of the electric field just outside the sphere. What is the electric flux through a spherical surface just inside the inner surface of the sphere?arrow_forwardA point charge of -3.00 μC is located in the center of a spherical cavity of radius 6.60 cm inside an insulating spherical charged solid. The charge density in the solid is 7.35 × 10−4 C/m3. Calculate the magnitude of the electric field inside the solid at a distance of 9.10 cm from the center of the cavity. Find the direction of this electric field.arrow_forwardAn infinitely long conducting cylindrical rod with a positive charge λ per unit length is surrounded by a conducting cylindrical shell (which is also infinitely long) with a charge per unit length of −2λ and radius r1, as shown in the figure. What is E(r), the radial component of the electric field between the rod and cylindrical shell as a function of the distance r from the axis of the cylindrical rod? Express your answer in terms of λ, r, and ϵ0, the permittivity of free space. What is σinner, the surface charge density (charge per unit area) on the inner surface of the conducting shell? What is σouterσouter, the surface charge density on the outside of the conducting shell? (Recall from the problem statement that the conducting shell has a total charge per unit length given by −2λ.) What is the radial component of the electric field, E(r), outside the shell?arrow_forward
- A very long conducting tube (hollow cylinder) has inner radius aa and outer radius b. It carries charge per unit length +α, where αα is a positive constant with units of C/m. A line of charge lies along the axis of the tube. The line of charge has charge per unit length +α. Calculate the electric field in terms of α and the distance r from the axis of the tube for r<a. Calculate the electric field in terms of α and the distance rr from the axis of the tube for a<r<b. Calculate the electric field in terms of αα and the distance r from the axis of the tube for r>b. What is the charge per unit length on the inner surface of the tube? What is the charge per unit length on the outer surface of the tube?arrow_forwardTwo small insulating spheres with radius 9.00×10−2 m are separated by a large center-to-center distance of 0.545 m . One sphere is negatively charged, with net charge -1.75 μC , and the other sphere is positively charged, with net charge 3.70 μC . The charge is uniformly distributed within the volume of each sphere. What is the magnitude E of the electric field midway between the spheres? Take the permittivity of free space to be ϵ0 = 8.85×10−12 C2/(N⋅m2) . What is the direction of the electric field midway between the spheres?arrow_forwardA conducting spherical shell with inner radius aa and outer radius bb has a positive point charge Q located at its center. The total charge on the shell is -3Q, and it is insulated from its surroundings. Derive the expression for the electric field magnitude in terms of the distance r from the center for the region r<a. Express your answer in terms of some or all of the variables Q, a, b, and appropriate constants. Derive the expression for the electric field magnitude in terms of the distance rr from the center for the region a<r<b. Derive the expression for the electric field magnitude in terms of the distance rr from the center for the region r>b. What is the surface charge density on the inner surface of the conducting shell? What is the surface charge density on the outer surface of the conducting shell?arrow_forward
- A small sphere with a mass of 3.00×10−3 g and carrying a charge of 4.80×10−8 C hangs from a thread near a very large, charged insulating sheet, as shown in the figure (Figure 1). The charge density on the sheet is −2.20×10−9 C/m2 . Find the angle of the thread.arrow_forwardA small conducting spherical shell with inner radius aa and outer radius bb is concentric with a larger conducting spherical shell with inner radius c and outer radius d (Figure 1). The inner shell has total charge +2q, and the outer shell has charge −2q. Calculate the magnitude of the electric field in terms of q and the distance rr from the common center of the two shells for r<a. Calculate the magnitude of the electric field for a<r<b. Calculate the magnitude of the electric field for b<r<c.arrow_forwardA cube has sides of length L = 0.800 m . It is placed with one corner at the origin as shown in the figure. The electric field is not uniform but is given by E→=αxi^+βzk^, where α=−3.90 and β= 7.10. What is the sum of the flux through the surface S5 and S6? What is the sum of the flux through the surface S2 and S4? Find the total electric charge inside the cube.arrow_forward
 College PhysicsPhysicsISBN:9781938168000Author:Paul Peter Urone, Roger HinrichsPublisher:OpenStax College
College PhysicsPhysicsISBN:9781938168000Author:Paul Peter Urone, Roger HinrichsPublisher:OpenStax College
 Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning College PhysicsPhysicsISBN:9781305952300Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning
College PhysicsPhysicsISBN:9781305952300Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning College PhysicsPhysicsISBN:9781285737027Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning
College PhysicsPhysicsISBN:9781285737027Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning Physics for Scientists and Engineers, Technology ...PhysicsISBN:9781305116399Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers, Technology ...PhysicsISBN:9781305116399Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning





