
An ideal gas with specific heat ratio γ confined to a cylinder is put through a closed cycle. Initially, the gas is at Pi, Vi, and Ti. First, its pressure is tripled under constant volume. It then expands adiabatically to its original pressure and finally is compressed isobarically to its original volume. (a) Draw a PV diagram of this cycle. (b) Determine the volume at the end of the adiabatic expansion. Find (c) the temperature of the gas at the start of the adiabatic expansion and (d) the temperature at the end of the cycle. (e) What was the net work done on the gas for this cycle?
(a)
Draw the
Answer to Problem 48P
The
Explanation of Solution
In this cycle, from
From
Figure 1 is the
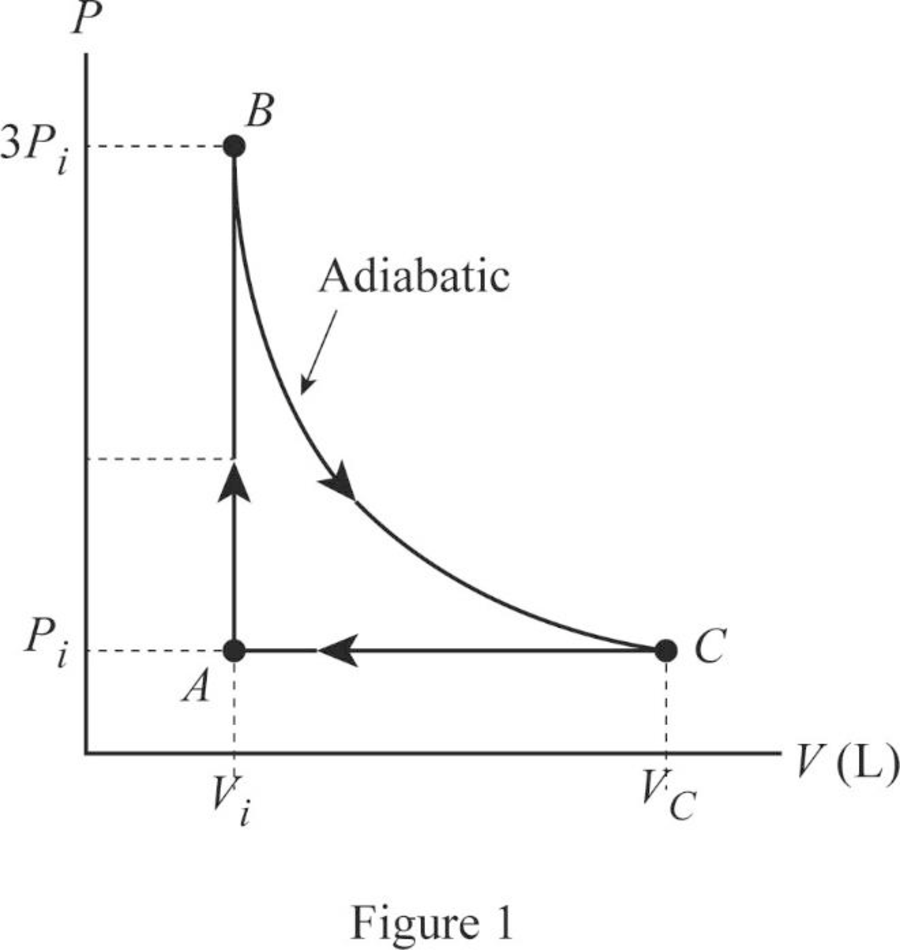
Conclusion:
Therefore, the
(b)
The volume of the gas at the end of the adiabatic expansion.
Answer to Problem 48P
The volume of the gas at the end of the adiabatic expansion is
Explanation of Solution
Write the expression for the adiabatic process,
Here,
Conclusion:
Substitute
Rewrite the above equation for
Therefore, the volume of the gas at the end of the adiabatic expansion is
(c)
The temperature of the gas at the start of the expansion.
Answer to Problem 48P
The temperature of the gas at the start of the expansion is
Explanation of Solution
Write the expression for the ideal gas law,
Conclusion:
Substitute
Therefore, the temperature of the gas at the start of the expansion is
(d)
The temperature at the end of the cycle.
Answer to Problem 48P
The temperature at the end of the cycle is
Explanation of Solution
In this case, starting point is
Write the expression for the temperature at the end of the cycle,
Conclusion:
Therefore, the temperature at the end of the cycle is
(e)
The net work done on the gas during the cycle.
Answer to Problem 48P
The net work done on the gas during the cycle is
Explanation of Solution
Write the expression for the heat transferred during the cycle
Here,
Substitute
In an adiabatic process,
Here,
Write the expression for the ideal gas law,
Substitute
Write the expression for the heat transferred during the cycle
Here,
Substitute
Write the expression for the heat transferred for whole cycle,
Here,
Substitute (V), (VI) and (XII) in (XIII),
Write the expression for the internal energy change in the whole cycle,
Write the expression for the net work done on the gas during the cycle,
Conclusion:
Substitute
Therefore, the net work done on the gas during the cycle is
Want to see more full solutions like this?
Chapter 17 Solutions
Principles of Physics: A Calculus-Based Text
 Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Physics for Scientists and Engineers, Technology ...PhysicsISBN:9781305116399Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers, Technology ...PhysicsISBN:9781305116399Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning
Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning
 Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning





