
(a)
Draw the
(a)
Answer to Problem 47P
The
Explanation of Solution
In this cycle, from
From
The Figure 1 shown the
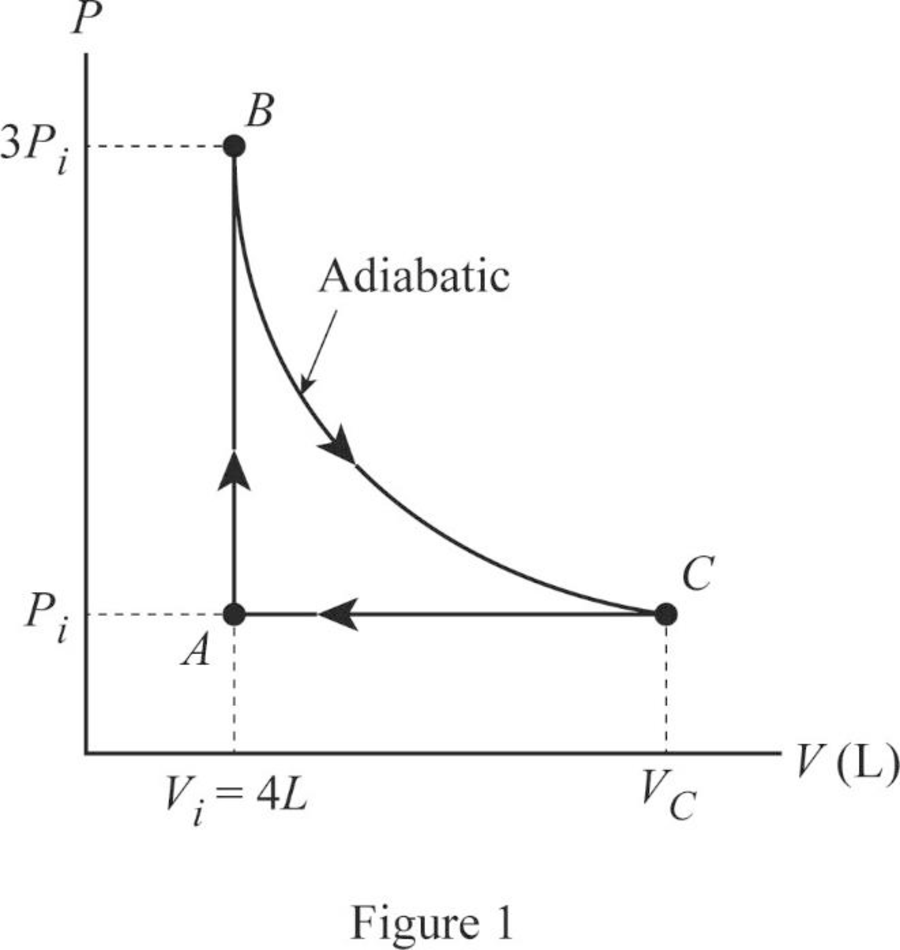
Conclusion:
Therefore, the
(b)
Thevolume of the gas at the end of the adiabatic expansion.
(b)
Answer to Problem 47P
The volume of the gas at the end of the adiabatic expansion is
Explanation of Solution
Write the expression for the adiabatic process,
Here,
Substitute
Rewrite the above equation for
Conclusion:
Substitute
Therefore, the volume of the gas at the end of the adiabatic expansion is
(c)
The temperature of the gas at the start of the expansion.
(c)
Answer to Problem 47P
Thetemperature of the gas at the start of the expansion is
Explanation of Solution
Write the expression for the
Substitute
Conclusion:
Substitute
Therefore, the temperature of the gas at the start of the expansion is
(d)
The temperature at the end of the cycle.
(d)
Answer to Problem 47P
Thetemperature at the end of the cycle is
Explanation of Solution
In this case, starting point is
Write the expression for the temperature at the end of the cycle,
Conclusion:
Substitute
Therefore, the temperature at the end of the cycle is
(e)
The net work done on the gas during the cycle.
(e)
Answer to Problem 47P
Thenet work done on the gas during the cycle is
Explanation of Solution
Write the expression for the
Here,
Substitute
In an adiabatic process,
Write the expression for the ideal gas law,
Substitute
Write the expression for the heat transferred during the cycle
Here,
Substitute
Write the expression for the heat transferredfor whole cycle,
Here,
Write the expression for the internal energy change in the whole cycle,
Write the expression for the net work done on the gas during the cycle,
Conclusion:
Substitute
Therefore, the net work done on the gas during the cycle is
Want to see more full solutions like this?
Chapter 17 Solutions
Principles of Physics: A Calculus-Based Text
- A filmmaker wants to achieve an interesting visual effect by filming a scene through a converging lens with a focal length of 50.0 m. The lens is placed betwen the camera and a horse, which canters toward the camera at a constant speed of 7.9 m/s. The camera starts rolling when the horse is 36.0 m from the lens. Find the average speed of the image of the horse (a) during the first 2.0 s after the camera starts rolling and (b) during the following 2.0 s.arrow_forwardAnswer the question (Physics)arrow_forwardsolve smybolically and plug in numbers and solve at the endarrow_forward
- answer the question symbolically until you have to plug in numbers. show all work please.arrow_forwardWhat is the direction of the magnetic force on a NEGATIVE CHARGE that moves as shown in each of the six cases?arrow_forwardHi! I need help with these calculations for part i and part k for a physics Diffraction Lab. We used a slit width 0.4 mm to measure our pattern.arrow_forward
- Examine the data and % error values in Data Table 3 where the angular displacement of the simple pendulum decreased but the mass of the pendulum bob and the length of the pendulum remained constant. Describe whether or not your data shows that the period of the pendulum depends on the angular displacement of the pendulum bob, to within a reasonable percent error.arrow_forwardIn addition to the anyalysis of the graph, show mathematically that the slope of that line is 2π/√g . Using the slope of your line calculate the value of g and compare it to 9.8.arrow_forwardAn object is placed 24.1 cm to the left of a diverging lens (f = -6.51 cm). A concave mirror (f= 14.8 cm) is placed 30.2 cm to the right of the lens to form an image of the first image formed by the lens. Find the final image distance, measured relative to the mirror. (b) Is the final image real or virtual? (c) Is the final image upright or inverted with respect to the original object?arrow_forward
- Concept Simulation 26.4 provides the option of exploring the ray diagram that applies to this problem. The distance between an object and its image formed by a diverging lens is 5.90 cm. The focal length of the lens is -2.60 cm. Find (a) the image distance and (b) the object distance.arrow_forwardPls help ASAParrow_forwardPls help ASAParrow_forward
 Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Physics for Scientists and Engineers, Technology ...PhysicsISBN:9781305116399Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers, Technology ...PhysicsISBN:9781305116399Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
 Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning
Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning





