Chapter 1.7, Problem 26E

a.

To determine

To graph: The given data in the form of a scatter plot.

Explanation of Solution

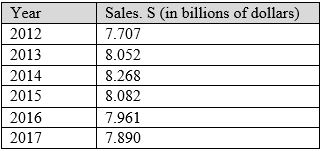
Given data for graph:

Graph:

By using a graphing utility, a scatter plot is drawn below for given data.

Interpretation:

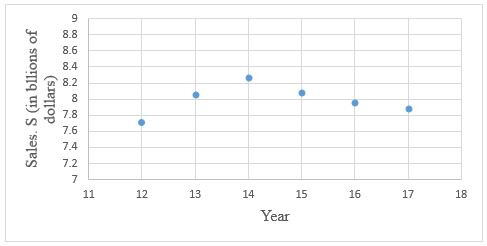
From the above graph, points $\left(12,7·707\right)$ , $\left(13,8·052\right)$ and $\left(14,8·268\right)$ are approximately linear.

Also, the points $\left(15,8·082\right)$ , $\left(16,7·961\right)$ and $\left(17,7·890\right)$ appear to be approximately linear.

Conclusion:

The given scatter plot shows an approximately even rise and fall in the annual sales.

b.

To determine

To find: A linear model using regression utility.

Explanation of Solution

Given data for graph:

Graph:

Interpretation:

The regression line shows the average movement of graph and has a positive slope thus indicating that the graph is growing upward despite the three downward movement in year 2015, 2016 and 2017.

c.

To determine

To write: A piecewise-defined model for the given data.

Explanation of Solution

Given data for graph:

Given data can be represented as a piecewise-defined model by adding certain conditions for each line formed between two points.

In the graph for the year 2012 and 2013 the slope of the line is $8.052-7.707=0.345$ .

Using slope point equation of line for the year 2012-2013 it can be written as

  $\begin{array}{c}{y}_2-y_1=m(x_2-x_1)\\ y_2-8.052=0.345(x_2-13)\\ y_2-8.052=0.345x_2-0.345\times 13\\ y_2-8.052=0.345x_2-4.485\\ y_2=0.345x_2+3.567\end{array}$

  $\Rightarrow f(x)=0.345x+3.567$ For $13\ge x\ge 12$

Similarly for the year 2013-2014 slope comes out to be $\mathrm{0.216.}$

  $\begin{array}{c}{y}_2-y_1=m(x_2-x_1)\\ y_2-8.268=0.216(x_2-14)\\ y_2-8.268=0.216x_2-0.216*14\\ y_2-8.268=0.216x_2-3.024\\ y_2=0.216x_2+5.244\end{array}$

  $\Rightarrow f(x)=0.216x+5.244$ for $14\ge x\ge 13$

  

For the year 2014-2015, slope is $–\mathrm{0.186.}$

  $\Rightarrow f(x)=-0.186x+10.872$ for $15\ge x\ge 14$

For the year 2015-2016, slope of line comes out to be $-\mathrm{0.121.}$

  $\begin{array}{c}{y}_2-y_1=m(x_2-x_1)\\ y_2-7.961=-0.121(x_2-16)\\ y_2-7.961=-0.121x_2+0.121\times 16\\ y_2-7.961=-0.121x_2+1.936\\ y_2=-0.121x_2+9.897\end{array}$

  $\Rightarrow f(x)=-0.121x+9.897$ for $16\ge x\ge 15$

  

Finally, for the year 2016-2017, the slope is $-\mathrm{0.071.}$

  $\begin{array}{c}{y}_2-y_1=m(x_2-x_1)\\ y_2-7.890=-0.071(x_2-17)\\ y_2-7.890=-0.071x_2+0.071\times 17\\ y_2-7.890=-0.071x_2+1.207\\ y_2=-0.071x_2+9.097\end{array}$

  $\Rightarrow f(x)=-0.071x+9.097$ for $17\ge x\ge 16$

d.

To determine

To find: The reason as to why a piecewise-defined model for the given data was possible.

Explanation of Solution

Given data for graph:

Piecewise-defined function was possible for the given set of data as points could be plotted from the data. On connecting any two points we get a line and as every line has one single equation we were able to plot a piecewise −defined function.

Line drawn between two points gives a close estimate for points lying in between these points.

Conclusion:

Piecewise-defined model helps in studying a single phase/part of a graph.

Piecewise-model can be possible only if the graph cannot be satisfied by a single equation or condition.