Chapter 1.3, Problem 112E

(a)

To determine

To find: The complete graph of the function when the function is odd.

Answer to Problem 112E

The complete graph of the function is shown in Figure(1).

Explanation of Solution

Given information:

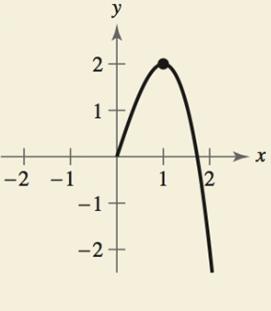
The function is odd and half graph of the function is given below:

  

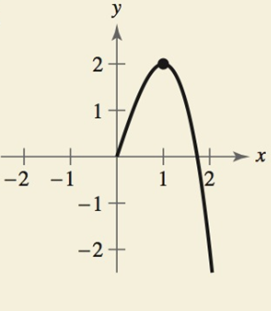
Calculation:

As the given function is odd, so the graph of the odd function is always symmetric about origin.

So, take the symmetric graph about the origin and complete the graph.

The complete graph taken by reflection in origin is given below:

  

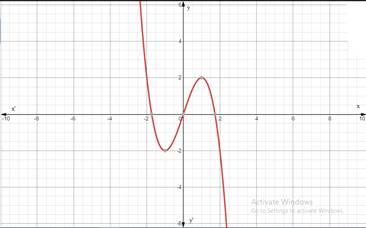
Figure(1)

(b)

To determine

To find: The domain and range of the function.

Answer to Problem 112E

The domain and range of the function are both equal to $\left(-\infty ,\infty \right)$ .

Explanation of Solution

Given information:

The function is odd and half graph of the function is given below:

  

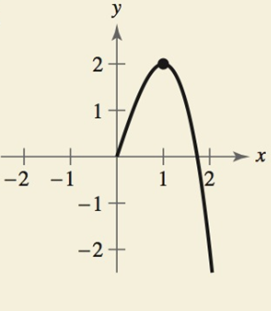
Calculation:

As observed from the graph in part(a), the function is defined for all the real values of $x$ .

So, the domain of the function is equal to $\left(-\infty ,\infty \right)$ .

As observed from the graph in part(a), the values of $y$ can be any real number.

So, the range of the function is also equal to $\left(-\infty ,\infty \right)$ .

Therefore, the domain and range of the function are both equal to $\left(-\infty ,\infty \right)$ .

(c)

To determine

To find: The intervals on which the function is increasing, decreasing or constant.

Answer to Problem 112E

The function is increasing on the interval $\left[-1,1\right]$ and decreasing on the interval $\left(-\infty ,-1\right]\cup \left[1,\infty \right)$ .

Explanation of Solution

Given information:

The function is odd and half graph of the function is given below:

  

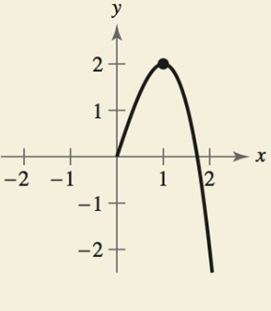
Calculation:

As observed from the graph in part(a), the function is increasing from $x=-1$ to the point $x=1$ .

As observed from the graph in part(a), the function is decreasing from $x=-\infty$ to the point $x=-1$ and then decreasing from $x=1$ onwards.

Therefore, the function is increasing on the interval $\left[-1,1\right]$ and decreasing on the interval $\left(-\infty ,-1\right]\cup \left[1,\infty \right)$ .

(d)

To determine

To find: The relative maximum and minimum values of the function.

Answer to Problem 112E

The relative maximum value of the function is $2$ at $x=1$ and relative minimum value of the function is $-2$ at $x=-1$ .

Explanation of Solution

Given information:

The function is odd and half graph of the function is given below:

  

Calculation:

As observed from the graph in part(a), the function achieves a relative maximum value at $x=1$ and the value of function at $x=1$ is equal to $2$ .

So, the relative maximum value of the function is equal to $2$ .

As observed from the graph in part(a), the function achieves a relative minimum value at $x=-1$ and the value of function at $x=-1$ is equal to $-2$ .

So, the relative minimum value of the function is equal to $-2$ .

Therefore, the relative maximum value of the function is $2$ at $x=1$ and relative minimum value of the function is $-2$ at $x=-1$ .