Chapter 1.7, Problem 24E

(a)

To determine

To graph: the data given in the table.

Explanation of Solution

Given data:

Table of year v/s Number of stores.

Graph:

Graph for the given table:

  

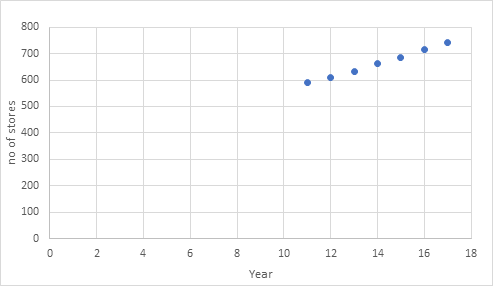
Conclusion:

It is a increasing graph.

(b)

To determine

Linear regression of graph.

Answer to Problem 24E

Linear regression of model is $y=24.8x+319.2$

Explanation of Solution

Given data:

Table of year v/s Number of stores.

Formula used:

Slope intercept form:

  $\begin{array}{l}y=mx+C\\ m=\frac{y_2-y_1}{x_2-x_1}\end{array}$

Calculation:

Linear regression of the model:

  $\begin{array}{l}y=mx+C\\ m=\frac{y_2-y_1}{x_2-x_1}\\ m=\frac{741-592}{2017-2011}\\ m=\frac{149}{6}\\ m=24.8\\ C=319.2\\ \\ y=24.8x+319.2\end{array}$

Conclusion:

Linear regression of model is $y=24.8x+319.2$

(c)

To determine

To find: Table of linear model values and original values.

Explanation of Solution

Given data:

Table of year v/s Number of stores.

Formula used:

Slope intercept form:

  $\begin{array}{l}y=mx+C\\ m=\frac{y_2-y_1}{x_2-x_1}\end{array}$

Calculation:

Table of model values and original values:

Year	Original values	Model values	Difference
2011	592	592	0
2012	608	617	9
2013	634	642	8
2014	663	666	3
2015	686	691	5
2016	715	716	1
2017	741	741	0

(d)

To determine

To find: whether the regression model a good fir or not

Answer to Problem 24E

Yes it is a good fit.

Explanation of Solution

Given data:

Table of year v/s Number of stores.

Formula used:

Slope intercept form:

  $\begin{array}{l}y=mx+C\\ m=\frac{y_2-y_1}{x_2-x_1}\end{array}$

Calculation:

Yes this is a good fit because line of fit is having value nearly to all original values.

  

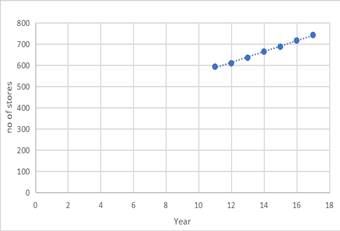
Conclusion:

Yes it is a good fit.

(e)

To determine

Number of stores for 2021

Answer to Problem 24E

Number of stores for 2021 will be 840 stores.

Explanation of Solution

Given data:

Table of year v/s Number of stores.

Formula used:

Slope intercept form:

  $\begin{array}{l}y=mx+C\\ m=\frac{y_2-y_1}{x_2-x_1}\end{array}$

Calculation:

Number of stores for 2021 will be:

  $\begin{array}{l}y=24.8x+319.2\\ y=24.8(21)+319.2\\ y=840\text{stores}\end{array}$

It is a reasonable answer because as the graph is increasing with year.

Conclusion:

Number of stores for 2021 will be 840 stores.