EP PRECALC.GRAPHING APPR.-WEBASSIGN-1YR
8th Edition
ISBN: 9780357022078
Author: Larson
Publisher: CENGAGE L
expand_more
expand_more
format_list_bulleted
Videos
Question
Chapter 1.1, Problem 129E
a.
To determine
To graph: The data given and the graph the model.
a.
Expert Solution
Explanation of Solution
Given:
Following data is given in the form of a table
| Year | Bachelor’s degrees, B (in thousands) |
| 2005 | 826 |
| 2006 | 855 |
| 2007 | 875 |
| 2008 | 895 |
| 2009 | 916 |
| 2010 | 943 |
| 2011 | 982 |
| 2012 | 1026 |
| 2013 | 1053 |
| 2014 | 1068 |
| 2015 | 1082 |
| 2016 | 1099 |
The data can be approximated by the linear model
Graph:
By using the above data, points and the model can be plotted as
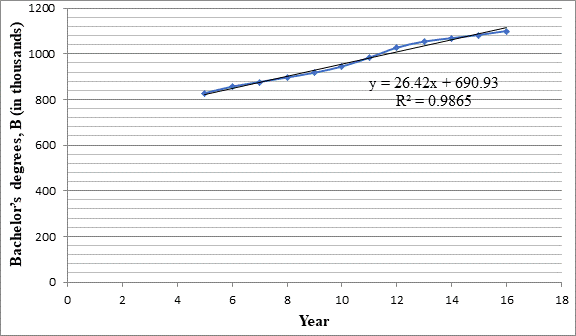
Interpretation:
The graph shows that the points plotted are very close to the graph of the linear model.
b.
To determine
To find: the bachelor’s degrees earned by women for each year from 2005 through 2016 by the linear model.
b.
Expert Solution
Explanation of Solution
Given:
The linear model
Calculation:
Table below shows the data for each year from 2005 to 2016.
| Year | Bachelor’s degrees, B (in thousands) |
| 2005 | 823 |
| 2006 | 849.42 |
| 2007 | 875.84 |
| 2008 | 902.26 |
| 2009 | 928.68 |
| 2010 | 955.1 |
| 2011 | 981.52 |
| 2012 | 1007.94 |
| 2013 | 1034.36 |
| 2014 | 1060.78 |
| 2015 | 1087.2 |
| 2016 | 1113.62 |
c.
To determine
To compare: the given data with the data obtained from linear model.
c.
Expert Solution
Explanation of Solution
Given:
Following data is given in the form of a table
| Year | Bachelor’s degrees, B (in thousands) |
| 2005 | 826 |
| 2006 | 855 |
| 2007 | 875 |
| 2008 | 895 |
| 2009 | 916 |
| 2010 | 943 |
| 2011 | 982 |
| 2012 | 1026 |
| 2013 | 1053 |
| 2014 | 1068 |
| 2015 | 1082 |
| 2016 | 1099 |
The data can be approximated by the linear model
Calculation:
| Year | Bachelor’s degrees, B (in thousands)
(data given) | Bachelor’s degrees, B (in thousands)
(data from the linear model ) | Difference between the two values |
| 2005 | 826 | 823 | 3 |
| 2006 | 855 | 849.42 | 5.58 |
| 2007 | 875 | 875.84 | -0.84 |
| 2008 | 895 | 902.26 | -7.62 |
| 2009 | 916 | 928.68 | -12.68 |
| 2010 | 943 | 955.1 | -12.1 |
| 2011 | 982 | 981.52 | 0.48 |
| 2012 | 1026 | 1007.94 | 18.06 |
| 2013 | 1053 | 1034.36 | 18.64 |
| 2014 | 1068 | 1060.78 | 7.22 |
| 2015 | 1082 | 1087.2 | -5.2 |
| 2016 | 1099 | 1113.62 | -14.62 |
As can be seen from the table, the difference between the given data and the data obtained from the linear model is very less thus; the model is best suited for the data.
d.
To determine
To find: the slope and the y -intercept of the model.
d.
Expert Solution
Explanation of Solution
Given:
The linear model:
Concept used; The equation of a straight line is given by
Calculation:
We have the equation of linear model as
Thus the slope of the model is,
Slope tells how much the value of y changes with the change in x .
The y -intercept of the linear model shows the value at t = 0, as we know t = 5 corresponds to 2005, t = 0 will correspond to 2000. Thus the y -intercept gives the number of bachelor’s degrees earned by women in the year 2000.
e.
To determine
To find: the number of bachelor’s degrees earned by women in the year 2022
e.
Expert Solution
Explanation of Solution
Given:
The linear model
Calculation:
t = 5 corresponds to 2005, therefore 2022 is given by t = 22,
Putting the value of t as 22 in the linear model we get,
Therefore, the number of bachelor’s degrees earned by women in the year 2022 is 1272.14 thousands
Chapter 1 Solutions
EP PRECALC.GRAPHING APPR.-WEBASSIGN-1YR
Ch. 1.1 - Prob. 1ECh. 1.1 - Prob. 2ECh. 1.1 - Prob. 3ECh. 1.1 - Prob. 4ECh. 1.1 - Prob. 5ECh. 1.1 - Prob. 6ECh. 1.1 - Prob. 7ECh. 1.1 - Prob. 8ECh. 1.1 - Prob. 9ECh. 1.1 - Prob. 10E
Ch. 1.1 - Prob. 11ECh. 1.1 - Prob. 12ECh. 1.1 - Prob. 13ECh. 1.1 - Prob. 14ECh. 1.1 - Prob. 15ECh. 1.1 - Prob. 16ECh. 1.1 - Prob. 17ECh. 1.1 - Prob. 18ECh. 1.1 - Prob. 19ECh. 1.1 - Prob. 20ECh. 1.1 - Prob. 21ECh. 1.1 - Prob. 22ECh. 1.1 - Prob. 23ECh. 1.1 - Prob. 24ECh. 1.1 - Prob. 25ECh. 1.1 - Prob. 26ECh. 1.1 - Prob. 27ECh. 1.1 - Prob. 28ECh. 1.1 - Prob. 29ECh. 1.1 - Prob. 30ECh. 1.1 - Prob. 31ECh. 1.1 - Prob. 32ECh. 1.1 - Prob. 33ECh. 1.1 - Prob. 34ECh. 1.1 - Prob. 35ECh. 1.1 - Prob. 36ECh. 1.1 - Prob. 37ECh. 1.1 - Prob. 38ECh. 1.1 - Prob. 39ECh. 1.1 - Prob. 40ECh. 1.1 - Prob. 41ECh. 1.1 - Prob. 42ECh. 1.1 - Prob. 43ECh. 1.1 - Prob. 44ECh. 1.1 - Prob. 45ECh. 1.1 - Prob. 46ECh. 1.1 - Prob. 47ECh. 1.1 - Prob. 48ECh. 1.1 - Prob. 49ECh. 1.1 - Prob. 50ECh. 1.1 - Prob. 51ECh. 1.1 - Prob. 52ECh. 1.1 - Prob. 53ECh. 1.1 - Prob. 54ECh. 1.1 - Prob. 55ECh. 1.1 - Prob. 56ECh. 1.1 - Prob. 57ECh. 1.1 - Prob. 58ECh. 1.1 - Prob. 59ECh. 1.1 - Prob. 60ECh. 1.1 - Prob. 61ECh. 1.1 - Prob. 62ECh. 1.1 - Prob. 63ECh. 1.1 - Prob. 64ECh. 1.1 - Prob. 65ECh. 1.1 - Prob. 66ECh. 1.1 - Prob. 67ECh. 1.1 - Prob. 68ECh. 1.1 - Prob. 69ECh. 1.1 - Prob. 70ECh. 1.1 - Prob. 71ECh. 1.1 - Prob. 72ECh. 1.1 - Prob. 73ECh. 1.1 - Prob. 74ECh. 1.1 - Prob. 75ECh. 1.1 - Prob. 76ECh. 1.1 - Prob. 77ECh. 1.1 - Prob. 78ECh. 1.1 - Prob. 79ECh. 1.1 - Prob. 80ECh. 1.1 - Prob. 81ECh. 1.1 - Prob. 82ECh. 1.1 - Prob. 83ECh. 1.1 - Prob. 84ECh. 1.1 - Prob. 85ECh. 1.1 - Prob. 86ECh. 1.1 - Prob. 87ECh. 1.1 - Prob. 88ECh. 1.1 - Prob. 89ECh. 1.1 - Prob. 90ECh. 1.1 - Prob. 91ECh. 1.1 - Prob. 92ECh. 1.1 - Prob. 93ECh. 1.1 - Prob. 94ECh. 1.1 - Prob. 95ECh. 1.1 - Prob. 96ECh. 1.1 - Prob. 97ECh. 1.1 - Prob. 98ECh. 1.1 - Prob. 99ECh. 1.1 - Prob. 100ECh. 1.1 - Prob. 101ECh. 1.1 - Prob. 102ECh. 1.1 - Prob. 103ECh. 1.1 - Prob. 104ECh. 1.1 - Prob. 105ECh. 1.1 - Prob. 106ECh. 1.1 - Prob. 107ECh. 1.1 - Prob. 108ECh. 1.1 - Prob. 109ECh. 1.1 - Prob. 110ECh. 1.1 - Prob. 111ECh. 1.1 - Prob. 112ECh. 1.1 - Prob. 113ECh. 1.1 - Prob. 114ECh. 1.1 - Prob. 115ECh. 1.1 - Prob. 116ECh. 1.1 - Prob. 117ECh. 1.1 - Prob. 118ECh. 1.1 - Prob. 119ECh. 1.1 - Prob. 120ECh. 1.1 - Prob. 121ECh. 1.1 - Prob. 122ECh. 1.1 - Prob. 123ECh. 1.1 - Prob. 124ECh. 1.1 - Prob. 125ECh. 1.1 - Prob. 126ECh. 1.1 - Prob. 127ECh. 1.1 - Prob. 128ECh. 1.1 - Prob. 129ECh. 1.2 - Prob. 1ECh. 1.2 - Prob. 2ECh. 1.2 - Prob. 3ECh. 1.2 - Prob. 4ECh. 1.2 - Prob. 5ECh. 1.2 - Prob. 6ECh. 1.2 - Prob. 7ECh. 1.2 - Prob. 8ECh. 1.2 - Prob. 9ECh. 1.2 - Prob. 10ECh. 1.2 - Prob. 11ECh. 1.2 - Prob. 12ECh. 1.2 - Prob. 13ECh. 1.2 - Prob. 14ECh. 1.2 - Prob. 15ECh. 1.2 - Prob. 16ECh. 1.2 - Prob. 17ECh. 1.2 - Prob. 18ECh. 1.2 - Prob. 19ECh. 1.2 - Prob. 20ECh. 1.2 - Prob. 21ECh. 1.2 - Prob. 22ECh. 1.2 - Prob. 23ECh. 1.2 - Prob. 24ECh. 1.2 - Prob. 25ECh. 1.2 - Prob. 26ECh. 1.2 - Prob. 27ECh. 1.2 - Prob. 28ECh. 1.2 - Prob. 29ECh. 1.2 - Prob. 30ECh. 1.2 - Prob. 31ECh. 1.2 - Prob. 32ECh. 1.2 - Prob. 33ECh. 1.2 - Prob. 34ECh. 1.2 - Prob. 35ECh. 1.2 - Prob. 36ECh. 1.2 - Prob. 37ECh. 1.2 - Prob. 38ECh. 1.2 - Prob. 39ECh. 1.2 - Prob. 40ECh. 1.2 - Prob. 41ECh. 1.2 - Prob. 42ECh. 1.2 - Prob. 43ECh. 1.2 - Prob. 44ECh. 1.2 - Prob. 45ECh. 1.2 - Prob. 46ECh. 1.2 - Prob. 47ECh. 1.2 - Prob. 48ECh. 1.2 - Prob. 49ECh. 1.2 - Prob. 50ECh. 1.2 - Prob. 51ECh. 1.2 - Prob. 52ECh. 1.2 - Prob. 53ECh. 1.2 - Prob. 54ECh. 1.2 - Prob. 55ECh. 1.2 - Prob. 56ECh. 1.2 - Prob. 57ECh. 1.2 - Prob. 58ECh. 1.2 - Prob. 59ECh. 1.2 - Prob. 60ECh. 1.2 - Prob. 61ECh. 1.2 - Prob. 62ECh. 1.2 - Prob. 63ECh. 1.2 - Prob. 64ECh. 1.2 - Prob. 65ECh. 1.2 - Prob. 66ECh. 1.2 - Prob. 67ECh. 1.2 - Prob. 68ECh. 1.2 - Prob. 69ECh. 1.2 - Prob. 70ECh. 1.2 - Prob. 71ECh. 1.2 - Prob. 72ECh. 1.2 - Prob. 73ECh. 1.2 - Prob. 74ECh. 1.2 - Prob. 75ECh. 1.2 - Prob. 76ECh. 1.2 - Prob. 77ECh. 1.2 - Prob. 78ECh. 1.2 - Prob. 79ECh. 1.2 - Prob. 80ECh. 1.2 - Prob. 81ECh. 1.2 - Prob. 82ECh. 1.2 - Prob. 83ECh. 1.2 - Prob. 84ECh. 1.2 - Prob. 85ECh. 1.2 - Prob. 86ECh. 1.2 - Prob. 87ECh. 1.2 - Prob. 88ECh. 1.2 - Prob. 89ECh. 1.2 - Prob. 90ECh. 1.2 - Prob. 91ECh. 1.2 - Prob. 92ECh. 1.2 - Prob. 93ECh. 1.2 - Prob. 94ECh. 1.2 - Prob. 95ECh. 1.2 - Prob. 96ECh. 1.2 - Prob. 97ECh. 1.2 - Prob. 98ECh. 1.3 - Prob. 1ECh. 1.3 - Prob. 2ECh. 1.3 - Prob. 3ECh. 1.3 - Prob. 4ECh. 1.3 - Prob. 5ECh. 1.3 - Prob. 6ECh. 1.3 - Prob. 7ECh. 1.3 - Prob. 8ECh. 1.3 - Prob. 9ECh. 1.3 - Prob. 10ECh. 1.3 - Prob. 11ECh. 1.3 - Prob. 12ECh. 1.3 - Prob. 13ECh. 1.3 - Prob. 14ECh. 1.3 - Prob. 15ECh. 1.3 - Prob. 16ECh. 1.3 - Prob. 17ECh. 1.3 - Prob. 18ECh. 1.3 - Prob. 19ECh. 1.3 - Prob. 20ECh. 1.3 - Prob. 21ECh. 1.3 - Prob. 22ECh. 1.3 - Prob. 23ECh. 1.3 - Prob. 24ECh. 1.3 - Prob. 25ECh. 1.3 - Prob. 26ECh. 1.3 - Prob. 27ECh. 1.3 - Prob. 28ECh. 1.3 - Prob. 29ECh. 1.3 - Prob. 30ECh. 1.3 - Prob. 31ECh. 1.3 - Prob. 32ECh. 1.3 - Prob. 33ECh. 1.3 - Prob. 34ECh. 1.3 - Prob. 35ECh. 1.3 - Prob. 36ECh. 1.3 - Prob. 37ECh. 1.3 - Prob. 38ECh. 1.3 - Prob. 39ECh. 1.3 - Prob. 40ECh. 1.3 - Prob. 41ECh. 1.3 - Prob. 42ECh. 1.3 - Prob. 43ECh. 1.3 - Prob. 44ECh. 1.3 - Prob. 45ECh. 1.3 - Prob. 46ECh. 1.3 - Prob. 47ECh. 1.3 - Prob. 48ECh. 1.3 - Prob. 49ECh. 1.3 - Prob. 50ECh. 1.3 - Prob. 51ECh. 1.3 - Prob. 52ECh. 1.3 - Prob. 53ECh. 1.3 - Prob. 54ECh. 1.3 - Prob. 55ECh. 1.3 - Prob. 56ECh. 1.3 - Prob. 57ECh. 1.3 - Prob. 58ECh. 1.3 - Prob. 59ECh. 1.3 - Prob. 60ECh. 1.3 - Prob. 61ECh. 1.3 - Prob. 62ECh. 1.3 - Prob. 63ECh. 1.3 - Prob. 64ECh. 1.3 - Prob. 65ECh. 1.3 - Prob. 66ECh. 1.3 - Prob. 67ECh. 1.3 - Prob. 68ECh. 1.3 - Prob. 69ECh. 1.3 - Prob. 70ECh. 1.3 - Prob. 71ECh. 1.3 - Prob. 72ECh. 1.3 - Prob. 73ECh. 1.3 - Prob. 74ECh. 1.3 - Prob. 75ECh. 1.3 - Prob. 76ECh. 1.3 - Prob. 77ECh. 1.3 - Prob. 78ECh. 1.3 - Prob. 79ECh. 1.3 - Prob. 80ECh. 1.3 - Prob. 81ECh. 1.3 - Prob. 82ECh. 1.3 - Prob. 83ECh. 1.3 - Prob. 84ECh. 1.3 - Prob. 85ECh. 1.3 - Prob. 86ECh. 1.3 - Prob. 87ECh. 1.3 - Prob. 88ECh. 1.3 - Prob. 89ECh. 1.3 - Prob. 90ECh. 1.3 - Prob. 91ECh. 1.3 - Prob. 92ECh. 1.3 - Prob. 93ECh. 1.3 - Prob. 94ECh. 1.3 - Prob. 95ECh. 1.3 - Prob. 96ECh. 1.3 - Prob. 97ECh. 1.3 - Prob. 98ECh. 1.3 - Prob. 99ECh. 1.3 - Prob. 100ECh. 1.3 - Prob. 101ECh. 1.3 - Prob. 102ECh. 1.3 - Prob. 103ECh. 1.3 - Prob. 104ECh. 1.3 - Prob. 105ECh. 1.3 - Prob. 106ECh. 1.3 - Prob. 107ECh. 1.3 - Prob. 108ECh. 1.3 - Prob. 109ECh. 1.3 - Prob. 110ECh. 1.3 - Prob. 111ECh. 1.3 - Prob. 112ECh. 1.3 - Prob. 113ECh. 1.3 - Prob. 114ECh. 1.3 - Prob. 115ECh. 1.3 - Prob. 116ECh. 1.3 - Prob. 117ECh. 1.3 - Prob. 118ECh. 1.3 - Prob. 119ECh. 1.3 - Prob. 120ECh. 1.3 - Prob. 121ECh. 1.3 - Prob. 122ECh. 1.4 - Prob. 1ECh. 1.4 - Prob. 2ECh. 1.4 - Prob. 3ECh. 1.4 - Prob. 4ECh. 1.4 - Prob. 5ECh. 1.4 - Prob. 6ECh. 1.4 - Prob. 7ECh. 1.4 - Prob. 8ECh. 1.4 - Prob. 9ECh. 1.4 - Prob. 10ECh. 1.4 - Prob. 11ECh. 1.4 - Prob. 12ECh. 1.4 - Prob. 13ECh. 1.4 - Prob. 14ECh. 1.4 - Prob. 15ECh. 1.4 - Prob. 16ECh. 1.4 - Prob. 17ECh. 1.4 - Prob. 18ECh. 1.4 - Prob. 19ECh. 1.4 - Prob. 20ECh. 1.4 - Prob. 21ECh. 1.4 - Prob. 22ECh. 1.4 - Prob. 23ECh. 1.4 - Prob. 24ECh. 1.4 - Prob. 25ECh. 1.4 - Prob. 26ECh. 1.4 - Prob. 27ECh. 1.4 - Prob. 28ECh. 1.4 - Prob. 29ECh. 1.4 - Prob. 30ECh. 1.4 - Prob. 31ECh. 1.4 - Prob. 32ECh. 1.4 - Prob. 33ECh. 1.4 - Prob. 34ECh. 1.4 - Prob. 35ECh. 1.4 - Prob. 36ECh. 1.4 - Prob. 37ECh. 1.4 - Prob. 38ECh. 1.4 - Prob. 39ECh. 1.4 - Prob. 40ECh. 1.4 - Prob. 41ECh. 1.4 - Prob. 42ECh. 1.4 - Prob. 43ECh. 1.4 - Prob. 44ECh. 1.4 - Prob. 45ECh. 1.4 - Prob. 46ECh. 1.4 - Prob. 47ECh. 1.4 - Prob. 48ECh. 1.4 - Prob. 49ECh. 1.4 - Prob. 50ECh. 1.4 - Prob. 51ECh. 1.4 - Prob. 52ECh. 1.4 - Prob. 53ECh. 1.4 - Prob. 54ECh. 1.4 - Prob. 55ECh. 1.4 - Prob. 56ECh. 1.4 - Prob. 57ECh. 1.4 - Prob. 58ECh. 1.4 - Prob. 59ECh. 1.4 - Prob. 60ECh. 1.4 - Prob. 61ECh. 1.4 - Prob. 62ECh. 1.4 - Prob. 63ECh. 1.4 - Prob. 64ECh. 1.4 - Prob. 65ECh. 1.4 - Prob. 66ECh. 1.4 - Prob. 67ECh. 1.4 - Prob. 68ECh. 1.4 - Prob. 69ECh. 1.4 - Prob. 70ECh. 1.4 - Prob. 71ECh. 1.4 - Prob. 72ECh. 1.4 - Prob. 73ECh. 1.4 - Prob. 74ECh. 1.4 - Prob. 75ECh. 1.4 - Prob. 76ECh. 1.4 - Prob. 77ECh. 1.4 - Prob. 78ECh. 1.4 - Prob. 79ECh. 1.4 - Prob. 80ECh. 1.4 - Prob. 81ECh. 1.4 - Prob. 82ECh. 1.4 - Prob. 83ECh. 1.4 - Prob. 84ECh. 1.5 - Prob. 1ECh. 1.5 - Prob. 2ECh. 1.5 - Prob. 3ECh. 1.5 - Prob. 4ECh. 1.5 - Prob. 5ECh. 1.5 - Prob. 6ECh. 1.5 - Prob. 7ECh. 1.5 - Prob. 8ECh. 1.5 - Prob. 9ECh. 1.5 - Prob. 10ECh. 1.5 - Prob. 11ECh. 1.5 - Prob. 12ECh. 1.5 - Prob. 13ECh. 1.5 - Prob. 14ECh. 1.5 - Prob. 15ECh. 1.5 - Prob. 16ECh. 1.5 - Prob. 17ECh. 1.5 - Prob. 18ECh. 1.5 - Prob. 19ECh. 1.5 - Prob. 20ECh. 1.5 - Prob. 21ECh. 1.5 - Prob. 22ECh. 1.5 - Prob. 23ECh. 1.5 - Prob. 24ECh. 1.5 - Prob. 25ECh. 1.5 - Prob. 26ECh. 1.5 - Prob. 27ECh. 1.5 - Prob. 28ECh. 1.5 - Prob. 29ECh. 1.5 - Prob. 30ECh. 1.5 - Prob. 31ECh. 1.5 - Prob. 32ECh. 1.5 - Prob. 33ECh. 1.5 - Prob. 34ECh. 1.5 - Prob. 35ECh. 1.5 - Prob. 36ECh. 1.5 - Prob. 37ECh. 1.5 - Prob. 38ECh. 1.5 - Prob. 39ECh. 1.5 - Prob. 40ECh. 1.5 - Prob. 41ECh. 1.5 - Prob. 42ECh. 1.5 - Prob. 43ECh. 1.5 - Prob. 44ECh. 1.5 - Prob. 45ECh. 1.5 - Prob. 46ECh. 1.5 - Prob. 47ECh. 1.5 - Prob. 48ECh. 1.5 - Prob. 49ECh. 1.5 - Prob. 50ECh. 1.5 - Prob. 51ECh. 1.5 - Prob. 52ECh. 1.5 - Prob. 53ECh. 1.5 - Prob. 54ECh. 1.5 - Prob. 55ECh. 1.5 - Prob. 56ECh. 1.5 - Prob. 57ECh. 1.5 - Prob. 58ECh. 1.5 - Prob. 59ECh. 1.5 - Prob. 60ECh. 1.5 - Prob. 61ECh. 1.5 - Prob. 62ECh. 1.5 - Prob. 63ECh. 1.5 - Prob. 64ECh. 1.5 - Prob. 65ECh. 1.5 - Prob. 66ECh. 1.5 - Prob. 67ECh. 1.5 - Prob. 68ECh. 1.5 - Prob. 69ECh. 1.5 - Prob. 70ECh. 1.5 - Prob. 71ECh. 1.5 - Prob. 72ECh. 1.5 - Prob. 73ECh. 1.5 - Prob. 74ECh. 1.5 - Prob. 75ECh. 1.5 - Prob. 76ECh. 1.5 - Prob. 77ECh. 1.5 - Prob. 78ECh. 1.5 - Prob. 79ECh. 1.5 - Prob. 80ECh. 1.5 - Prob. 81ECh. 1.5 - Prob. 82ECh. 1.5 - Prob. 83ECh. 1.5 - Prob. 84ECh. 1.5 - Prob. 85ECh. 1.5 - Prob. 86ECh. 1.5 - Prob. 87ECh. 1.5 - Prob. 88ECh. 1.5 - Prob. 89ECh. 1.5 - Prob. 90ECh. 1.5 - Prob. 91ECh. 1.5 - Prob. 92ECh. 1.5 - Prob. 93ECh. 1.5 - Prob. 94ECh. 1.5 - Prob. 95ECh. 1.5 - Prob. 96ECh. 1.5 - Prob. 97ECh. 1.5 - Prob. 98ECh. 1.5 - Prob. 99ECh. 1.5 - Prob. 100ECh. 1.5 - Prob. 101ECh. 1.5 - Prob. 102ECh. 1.6 - Prob. 1ECh. 1.6 - Prob. 2ECh. 1.6 - Prob. 3ECh. 1.6 - Prob. 4ECh. 1.6 - Prob. 5ECh. 1.6 - Prob. 6ECh. 1.6 - Prob. 7ECh. 1.6 - Prob. 8ECh. 1.6 - Prob. 9ECh. 1.6 - Prob. 10ECh. 1.6 - Prob. 11ECh. 1.6 - Prob. 12ECh. 1.6 - Prob. 13ECh. 1.6 - Prob. 14ECh. 1.6 - Prob. 15ECh. 1.6 - Prob. 16ECh. 1.6 - Prob. 17ECh. 1.6 - Prob. 18ECh. 1.6 - Prob. 19ECh. 1.6 - Prob. 20ECh. 1.6 - Prob. 21ECh. 1.6 - Prob. 22ECh. 1.6 - Prob. 23ECh. 1.6 - Prob. 24ECh. 1.6 - Prob. 25ECh. 1.6 - Prob. 26ECh. 1.6 - Prob. 27ECh. 1.6 - Prob. 28ECh. 1.6 - Prob. 29ECh. 1.6 - Prob. 30ECh. 1.6 - Prob. 31ECh. 1.6 - Prob. 32ECh. 1.6 - Prob. 33ECh. 1.6 - Prob. 34ECh. 1.6 - Prob. 35ECh. 1.6 - Prob. 36ECh. 1.6 - Prob. 37ECh. 1.6 - Prob. 38ECh. 1.6 - Prob. 39ECh. 1.6 - Prob. 40ECh. 1.6 - Prob. 41ECh. 1.6 - Prob. 42ECh. 1.6 - Prob. 43ECh. 1.6 - Prob. 44ECh. 1.6 - Prob. 45ECh. 1.6 - Prob. 46ECh. 1.6 - Prob. 47ECh. 1.6 - Prob. 48ECh. 1.6 - Prob. 49ECh. 1.6 - Prob. 50ECh. 1.6 - Prob. 51ECh. 1.6 - Prob. 52ECh. 1.6 - Prob. 53ECh. 1.6 - Prob. 54ECh. 1.6 - Prob. 55ECh. 1.6 - Prob. 56ECh. 1.6 - Prob. 57ECh. 1.6 - Prob. 58ECh. 1.6 - Prob. 59ECh. 1.6 - Prob. 60ECh. 1.6 - Prob. 61ECh. 1.6 - Prob. 62ECh. 1.6 - Prob. 63ECh. 1.6 - Prob. 64ECh. 1.6 - Prob. 65ECh. 1.6 - Prob. 66ECh. 1.6 - Prob. 67ECh. 1.6 - Prob. 68ECh. 1.6 - Prob. 69ECh. 1.6 - Prob. 70ECh. 1.6 - Prob. 71ECh. 1.6 - Prob. 72ECh. 1.6 - Prob. 73ECh. 1.6 - Prob. 74ECh. 1.6 - Prob. 75ECh. 1.6 - Prob. 76ECh. 1.6 - Prob. 77ECh. 1.6 - Prob. 78ECh. 1.6 - Prob. 79ECh. 1.6 - Prob. 80ECh. 1.6 - Prob. 81ECh. 1.6 - Prob. 82ECh. 1.6 - Prob. 83ECh. 1.6 - Prob. 84ECh. 1.6 - Prob. 85ECh. 1.6 - Prob. 86ECh. 1.6 - Prob. 87ECh. 1.6 - Prob. 88ECh. 1.6 - Prob. 89ECh. 1.6 - Prob. 90ECh. 1.6 - Prob. 91ECh. 1.6 - Prob. 92ECh. 1.6 - Prob. 93ECh. 1.6 - Prob. 94ECh. 1.6 - Prob. 95ECh. 1.6 - Prob. 96ECh. 1.6 - Prob. 97ECh. 1.6 - Prob. 98ECh. 1.6 - Prob. 99ECh. 1.6 - Prob. 100ECh. 1.6 - Prob. 101ECh. 1.6 - Prob. 102ECh. 1.6 - Prob. 103ECh. 1.6 - Prob. 104ECh. 1.6 - Prob. 105ECh. 1.6 - Prob. 106ECh. 1.6 - Prob. 107ECh. 1.6 - Prob. 108ECh. 1.6 - Prob. 109ECh. 1.6 - Prob. 110ECh. 1.6 - Prob. 111ECh. 1.6 - Prob. 112ECh. 1.6 - Prob. 113ECh. 1.6 - Prob. 114ECh. 1.6 - Prob. 115ECh. 1.6 - Prob. 116ECh. 1.6 - Prob. 117ECh. 1.6 - Prob. 118ECh. 1.6 - Prob. 119ECh. 1.6 - Prob. 120ECh. 1.6 - Prob. 121ECh. 1.6 - Prob. 122ECh. 1.6 - Prob. 123ECh. 1.6 - Prob. 124ECh. 1.6 - Prob. 125ECh. 1.6 - Prob. 126ECh. 1.6 - Prob. 127ECh. 1.6 - Prob. 128ECh. 1.6 - Prob. 129ECh. 1.6 - Prob. 130ECh. 1.6 - Prob. 131ECh. 1.6 - Prob. 132ECh. 1.6 - Prob. 133ECh. 1.6 - Prob. 134ECh. 1.6 - Prob. 135ECh. 1.6 - Prob. 136ECh. 1.6 - Prob. 137ECh. 1.6 - Prob. 138ECh. 1.6 - Prob. 139ECh. 1.6 - Prob. 140ECh. 1.6 - Prob. 141ECh. 1.6 - Prob. 142ECh. 1.6 - Prob. 143ECh. 1.6 - Prob. 144ECh. 1.7 - Prob. 1ECh. 1.7 - Prob. 2ECh. 1.7 - Prob. 3ECh. 1.7 - Prob. 4ECh. 1.7 - Prob. 5ECh. 1.7 - Prob. 6ECh. 1.7 - Prob. 7ECh. 1.7 - Prob. 8ECh. 1.7 - Prob. 9ECh. 1.7 - Prob. 10ECh. 1.7 - Prob. 11ECh. 1.7 - Prob. 12ECh. 1.7 - Prob. 13ECh. 1.7 - Prob. 14ECh. 1.7 - Prob. 15ECh. 1.7 - Prob. 16ECh. 1.7 - Prob. 17ECh. 1.7 - Prob. 18ECh. 1.7 - Prob. 19ECh. 1.7 - Prob. 20ECh. 1.7 - Prob. 21ECh. 1.7 - Prob. 22ECh. 1.7 - Prob. 23ECh. 1.7 - Prob. 24ECh. 1.7 - Prob. 25ECh. 1.7 - Prob. 26ECh. 1.7 - Prob. 27ECh. 1.7 - Prob. 28ECh. 1.7 - Prob. 29ECh. 1.7 - Prob. 30ECh. 1.7 - Prob. 31ECh. 1.7 - Prob. 32ECh. 1.7 - Prob. 33ECh. 1.7 - Prob. 34ECh. 1 - Prob. 1CRCh. 1 - Prob. 2CRCh. 1 - Prob. 3CRCh. 1 - Prob. 4CRCh. 1 - Prob. 5CRCh. 1 - Prob. 6CRCh. 1 - Prob. 7CRCh. 1 - Prob. 8CRCh. 1 - Prob. 9CRCh. 1 - Prob. 10CRCh. 1 - Prob. 11CRCh. 1 - Prob. 12CRCh. 1 - Prob. 13CRCh. 1 - Prob. 14CRCh. 1 - Prob. 15CRCh. 1 - Prob. 16CRCh. 1 - Prob. 17CRCh. 1 - Prob. 18CRCh. 1 - Prob. 19CRCh. 1 - Prob. 20CRCh. 1 - Prob. 21CRCh. 1 - Prob. 22CRCh. 1 - Prob. 23CRCh. 1 - Prob. 24CRCh. 1 - Prob. 25CRCh. 1 - Prob. 26CRCh. 1 - Prob. 27CRCh. 1 - Prob. 28CRCh. 1 - Prob. 29CRCh. 1 - Prob. 30CRCh. 1 - Prob. 31CRCh. 1 - Prob. 32CRCh. 1 - Prob. 33CRCh. 1 - Prob. 34CRCh. 1 - Prob. 35CRCh. 1 - Prob. 36CRCh. 1 - Prob. 37CRCh. 1 - Prob. 38CRCh. 1 - Prob. 39CRCh. 1 - Prob. 40CRCh. 1 - Prob. 41CRCh. 1 - Prob. 42CRCh. 1 - Prob. 43CRCh. 1 - Prob. 44CRCh. 1 - Prob. 45CRCh. 1 - Prob. 46CRCh. 1 - Prob. 47CRCh. 1 - Prob. 48CRCh. 1 - Prob. 49CRCh. 1 - Prob. 50CRCh. 1 - Prob. 51CRCh. 1 - Prob. 52CRCh. 1 - Prob. 53CRCh. 1 - Prob. 54CRCh. 1 - Prob. 55CRCh. 1 - Prob. 56CRCh. 1 - Prob. 57CRCh. 1 - Prob. 58CRCh. 1 - Prob. 59CRCh. 1 - Prob. 60CRCh. 1 - Prob. 61CRCh. 1 - Prob. 62CRCh. 1 - Prob. 63CRCh. 1 - Prob. 64CRCh. 1 - Prob. 65CRCh. 1 - Prob. 66CRCh. 1 - Prob. 67CRCh. 1 - Prob. 68CRCh. 1 - Prob. 69CRCh. 1 - Prob. 70CRCh. 1 - Prob. 71CRCh. 1 - Prob. 72CRCh. 1 - Prob. 73CRCh. 1 - Prob. 74CRCh. 1 - Prob. 75CRCh. 1 - Prob. 76CRCh. 1 - Prob. 77CRCh. 1 - Prob. 78CRCh. 1 - Prob. 79CRCh. 1 - Prob. 80CRCh. 1 - Prob. 81CRCh. 1 - Prob. 82CRCh. 1 - Prob. 83CRCh. 1 - Prob. 84CRCh. 1 - Prob. 85CRCh. 1 - Prob. 86CRCh. 1 - Prob. 87CRCh. 1 - Prob. 88CRCh. 1 - Prob. 89CRCh. 1 - Prob. 90CRCh. 1 - Prob. 91CRCh. 1 - Prob. 92CRCh. 1 - Prob. 93CRCh. 1 - Prob. 94CRCh. 1 - Prob. 95CRCh. 1 - Prob. 96CRCh. 1 - Prob. 97CRCh. 1 - Prob. 98CRCh. 1 - Prob. 99CRCh. 1 - Prob. 100CRCh. 1 - Prob. 101CRCh. 1 - Prob. 102CRCh. 1 - Prob. 103CRCh. 1 - Prob. 104CRCh. 1 - Prob. 105CRCh. 1 - Prob. 106CRCh. 1 - Prob. 107CRCh. 1 - Prob. 108CRCh. 1 - Prob. 109CRCh. 1 - Prob. 110CRCh. 1 - Prob. 1CTCh. 1 - Prob. 2CTCh. 1 - Prob. 3CTCh. 1 - Prob. 4CTCh. 1 - Prob. 5CTCh. 1 - Prob. 6CTCh. 1 - Prob. 7CTCh. 1 - Prob. 8CTCh. 1 - Prob. 9CTCh. 1 - Prob. 10CTCh. 1 - Prob. 11CTCh. 1 - Prob. 12CTCh. 1 - Prob. 13CTCh. 1 - Prob. 14CTCh. 1 - Prob. 15CTCh. 1 - Prob. 16CTCh. 1 - Prob. 17CTCh. 1 - Prob. 18CTCh. 1 - Prob. 19CTCh. 1 - Prob. 20CT
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, calculus and related others by exploring similar questions and additional content below.Similar questions
- Solve the differential equation. 37 6 dy = 2x³y7 - 4x³ dxarrow_forwardFind an equation of the curve that passes through the point (0, 1) and whose slope at (x, y) is 3xy.arrow_forwardQ6. A fossil piece has been found in Alberta that contains 34% of C14 in it. What is the age of this fossil piece?arrow_forward
- Q5. Briefly explain what are isotopes of an elements, with an example, and why some isotopes are radioactive. 470arrow_forwardQ1. Will you earn more interest amount in two years by depositing $2000 in a simple interest account that pays 6% or in an account that pays 6.15% interest compounded monthly? tarrow_forwardQ4. We want to invest $18000 in an account compounded continuously. How long should the investment be kept so final value of the account reaches $25000 if the annual rate of interest is 5.8%?arrow_forward
- Q3. Determine the effective annual yield for each investment below. Then select the better investment. Assume 365 days in a year. a) 5.6% compounded semiannually; b) 5.4% compounded daily.arrow_forwardQ2. You deposit $22,000 in an account that pays 4.8% interest compounded monthly. a. Find the future value after six years. & b b. Determine the effective annual yield of this account.arrow_forward18. Using the method of variation of parameter, a particular solution to y′′ + 16y = 4 sec(4t) isyp(t) = u1(t) cos(4t) + u2(t) sin(4t). Then u2(t) is equal toA. 1 B. t C. ln | sin 4t| D. ln | cos 4t| E. sec(4t)arrow_forward
- Question 4. Suppose you need to know an equation of the tangent plane to a surface S at the point P(2, 1, 3). You don't have an equation for S but you know that the curves r1(t) = (2 + 3t, 1 — t², 3 − 4t + t²) r2(u) = (1 + u², 2u³ − 1, 2u + 1) both lie on S. (a) Check that both r₁ and r2 pass through the point P. 1 (b) Give the expression of the 074 in two ways Ət ⚫ in terms of 32 and 33 using the chain rule მყ ⚫ in terms of t using the expression of z(t) in the curve r1 (c) Similarly, give the expression of the 22 in two ways Əz ди ⚫ in terms of oz and oz using the chain rule Əz მყ • in terms of u using the expression of z(u) in the curve r2 (d) Deduce the partial derivative 32 and 33 at the point P and the equation of მე მყ the tangent planearrow_forwardCoast Guard Patrol Search Mission The pilot of a Coast Guard patrol aircraft on a search mission had just spotted a disabled fishing trawler and decided to go in for a closer look. Flying in a straight line at a constant altitude of 1000 ft and at a steady speed of 256 ft/s, the aircraft passed directly over the trawler. How fast (in ft/s) was the aircraft receding from the trawler when it was 1400 ft from the trawler? (Round your answer to one decimal places.) 1000 ft 180 × ft/s Need Help? Read It SUBMIT ANSWERarrow_forward6. The largest interval in which the solution of (cos t)y′′ +t^2y′ − (5/t)y = e^t/(t−3) , y(1) = 2, y′(1) = 0is guaranteed to exist by the Existence and Uniqueness Theorem is:A. (0, ∞) B. (π/2, 3) C. (0,π/2) D. (0, π) E. (0, 3)arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning
Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON
Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning
Calculus: Early Transcendentals
Calculus
ISBN:9781285741550
Author:James Stewart
Publisher:Cengage Learning
Thomas' Calculus (14th Edition)
Calculus
ISBN:9780134438986
Author:Joel R. Hass, Christopher E. Heil, Maurice D. Weir
Publisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)
Calculus
ISBN:9780134763644
Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric Schulz
Publisher:PEARSON
Calculus: Early Transcendentals
Calculus
ISBN:9781319050740
Author:Jon Rogawski, Colin Adams, Robert Franzosa
Publisher:W. H. Freeman
Calculus: Early Transcendental Functions
Calculus
ISBN:9781337552516
Author:Ron Larson, Bruce H. Edwards
Publisher:Cengage Learning
Maths - Geometry - What is an Angle - English; Author: Bodhaguru;https://www.youtube.com/watch?v=bsuDcCjFq6c;License: Standard YouTube License, CC-BY
What is an Angle? | Different Types of Angles | Geometry | Math | LetsTute; Author: Let'stute;https://www.youtube.com/watch?v=aGejx2fRCHU;License: Standard Youtube License