Chapter 1, Problem 97CR

(a)

To determine

To prove :f and g are inverse functions.

Explanation of Solution

Given data:

  $\begin{array}{l}f(x)=3-4x\\ g(x)=\frac{3-x}{4}\end{array}$

Calculation:

Algebraically,

Let f(x) be y

So,

  $\begin{array}{l}f(x)=3-4x\\ y=3-4x\\ for\text{ inverse function,}\\ \text{3-y}=\text{4x}\\ \text{x}=\frac{\text{3-y}}{\text{4}}\\ {\text{f}}^{\text{-1}}\text{(x)}=\frac{\text{3-x}}{4}\\ {\text{f}}^{\text{-1}}\text{(x)}=g(x)\end{array}$

G(x) is inverse function of f(x)

(b)

To determine

To prove :f and g are inverse function.

Explanation of Solution

Given data:

  $\begin{array}{l}f(x)=3-4x\\ g(x)=\frac{3-x}{4}\end{array}$

Calculation:

Graphically:

  

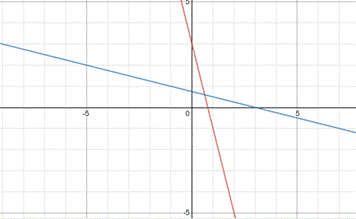
As the g(x) is the reflection of the f(x).

So g(x) is inverse function of f(x)

(c)

To determine

To prove: f and g are inverse function.

Explanation of Solution

Given data:

  $\begin{array}{l}f(x)=3-4x\\ g(x)=\frac{3-x}{4}\end{array}$

Calculation:

Numerically:

  $f(x)=3-4x\text{ ; }g(x)=\frac{3-x}{4}$

Domain of f(x): R Domain of g(x):R

Range of f(x):R Range of g(x):R

So g(x) is a inverse of f(x) as domain of f(x) is equal to range of g(x).

Conclusion:

G(x) is a inverse function of f(x)