Calculus 2012 Student Edition (by Finney/Demana/Waits/Kennedy)

4th Edition

ISBN: 9780133178579

Author: Ross L. Finney

Publisher: PEARSON

See similar textbooks

Videos

Question

Chapter 1.6, Problem 43E

(a)

To determine

To find: The amplitude of the model.

(a)

Expert Solution

Answer to Problem 43E

The amplitude of the model is 37 .

Explanation of Solution

Given information:

The given model is,

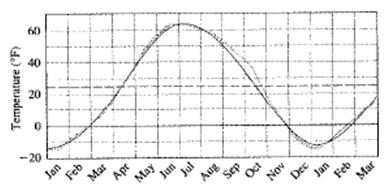
Calculus 2012 Student Edition (by Finney/Demana/Waits/Kennedy), Chapter 1.6, Problem 43E , additional homework tip 1

Calculation:

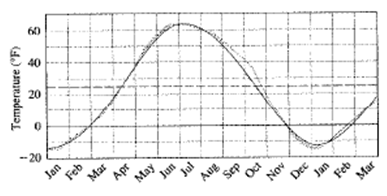
The amplitude is the half of the distance between highest and lowest curve. The highest temperature appears is 62° F and lowest is −12° F.

The amplitude can be calculated as:

A=62−(−12)2=742=37

Therefore, the amplitude is 37 .

(b)

To determine

To find: The period of the model.

(b)

Expert Solution

Answer to Problem 43E

The period of the model is 365 .

Explanation of Solution

Given information:

The given model is,

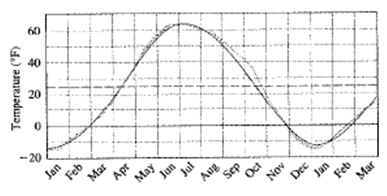
Calculus 2012 Student Edition (by Finney/Demana/Waits/Kennedy), Chapter 1.6, Problem 43E , additional homework tip 2

Calculation:

The period of the model can be calculated as:

period=2π(2π/365)=365

Therefore, the period of the model is 365 .

(c)

To determine

To find: The horizontal shift of the model.

(c)

Expert Solution

Answer to Problem 43E

The horizontal shift of the model is 101.

Explanation of Solution

Given information:

The given model is,

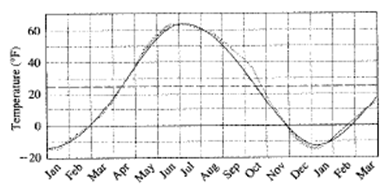
Calculus 2012 Student Edition (by Finney/Demana/Waits/Kennedy), Chapter 1.6, Problem 43E , additional homework tip 3

Calculate:

Horizontal shift is the distance of intersection point from the y -axis. From the graph it can be observed that the distance of intersection point from y -axis is 101. So, the horizontal shift of the model is 101 .

Therefore, the horizontal shift is 101 .

(d)

To determine

To find: The vertical shift of the model.

(d)

Expert Solution

Answer to Problem 43E

The vertical shift of the model is 25.

Explanation of Solution

Given information:

The given model is,

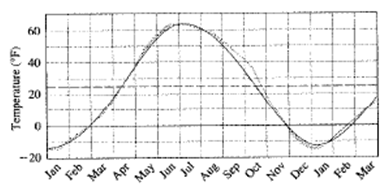
Calculus 2012 Student Edition (by Finney/Demana/Waits/Kennedy), Chapter 1.6, Problem 43E , additional homework tip 4

Calculate:

Vertical shift is the distance of intersection point from the x -axis. From the graph it can be observed that the distance of intersection point from x -axis is 25. So, the vertical shift of the model is 25.

Therefore, the vertical shift of the model is 25.

(e)

To determine

To find: The equation of the model.

(e)

Expert Solution

Answer to Problem 43E

The equation of the model is f(x)=37sin[2π365(x−101)]+25 .

Explanation of Solution

Given information:

The given model is,

Calculus 2012 Student Edition (by Finney/Demana/Waits/Kennedy), Chapter 1.6, Problem 43E , additional homework tip 5

Calculate:

The general equation for a function is:

y=Asin[2πB(x−C)]+D

Here, A is the amplitude, B is the period, C is the horizontal shift and D is the vertical shift.

So, the equation for the model is:

f(x)=37sin[2π365(x−101)]+25

Therefore, the equation of the model is f(x)=37sin[2π365(x−101)]+25 .

Chapter 1.6, Problem 42E

Chapter 1.6, Problem 44E

Chapter 1 Solutions

Calculus 2012 Student Edition (by Finney/Demana/Waits/Kennedy)

Ch. 1.1 - Prob. 1QR Ch. 1.1 - Prob. 2QR Ch. 1.1 - Prob. 3QR Ch. 1.1 - Prob. 4QR Ch. 1.1 - Prob. 5QR Ch. 1.1 - Prob. 6QR Ch. 1.1 - Prob. 7QR Ch. 1.1 - Prob. 8QR Ch. 1.1 - Prob. 9QR Ch. 1.1 - Prob. 10QR

Ch. 1.1 - Prob. 1E Ch. 1.1 - Prob. 2E Ch. 1.1 - Prob. 3E Ch. 1.1 - Prob. 4E Ch. 1.1 - Prob. 5E Ch. 1.1 - Prob. 6E Ch. 1.1 - Prob. 7E Ch. 1.1 - Prob. 8E Ch. 1.1 - Prob. 9E Ch. 1.1 - Prob. 10E Ch. 1.1 - Prob. 11E Ch. 1.1 - Prob. 12E Ch. 1.1 - Prob. 13E Ch. 1.1 - Prob. 14E Ch. 1.1 - Prob. 15E Ch. 1.1 - Prob. 16E Ch. 1.1 - Prob. 17E Ch. 1.1 - Prob. 18E Ch. 1.1 - Prob. 19E Ch. 1.1 - Prob. 20E Ch. 1.1 - Prob. 21E Ch. 1.1 - Prob. 22E Ch. 1.1 - Prob. 23E Ch. 1.1 - Prob. 24E Ch. 1.1 - Prob. 25E Ch. 1.1 - Prob. 26E Ch. 1.1 - Prob. 27E Ch. 1.1 - Prob. 28E Ch. 1.1 - Prob. 29E Ch. 1.1 - Prob. 30E Ch. 1.1 - Prob. 31E Ch. 1.1 - Prob. 32E Ch. 1.1 - Prob. 33E Ch. 1.1 - Prob. 34E Ch. 1.1 - Prob. 35E Ch. 1.1 - Prob. 36E Ch. 1.1 - Prob. 37E Ch. 1.1 - Prob. 38E Ch. 1.1 - Prob. 39E Ch. 1.1 - Prob. 40E Ch. 1.1 - Prob. 41E Ch. 1.1 - Prob. 42E Ch. 1.1 - Prob. 43E Ch. 1.1 - Prob. 44E Ch. 1.1 - Prob. 45E Ch. 1.1 - Prob. 46E Ch. 1.1 - Prob. 47E Ch. 1.1 - Prob. 48E Ch. 1.1 - Prob. 49E Ch. 1.1 - Prob. 50E Ch. 1.1 - Prob. 51E Ch. 1.1 - Prob. 52E Ch. 1.1 - Prob. 53E Ch. 1.1 - Prob. 54E Ch. 1.1 - Prob. 55E Ch. 1.1 - Prob. 56E Ch. 1.1 - Prob. 57E Ch. 1.1 - Prob. 58E Ch. 1.2 - Prob. 1QR Ch. 1.2 - Prob. 2QR Ch. 1.2 - Prob. 3QR Ch. 1.2 - Prob. 4QR Ch. 1.2 - Prob. 5QR Ch. 1.2 - Prob. 6QR Ch. 1.2 - Prob. 7QR Ch. 1.2 - Prob. 8QR Ch. 1.2 - Prob. 9QR Ch. 1.2 - Prob. 10QR Ch. 1.2 - Prob. 11QR Ch. 1.2 - Prob. 12QR Ch. 1.2 - Prob. 1E Ch. 1.2 - Prob. 2E Ch. 1.2 - Prob. 3E Ch. 1.2 - Prob. 4E Ch. 1.2 - Prob. 5E Ch. 1.2 - Prob. 6E Ch. 1.2 - Prob. 7E Ch. 1.2 - Prob. 8E Ch. 1.2 - Prob. 9E Ch. 1.2 - Prob. 10E Ch. 1.2 - Prob. 11E Ch. 1.2 - Prob. 12E Ch. 1.2 - Prob. 13E Ch. 1.2 - Prob. 14E Ch. 1.2 - Prob. 15E Ch. 1.2 - Prob. 16E Ch. 1.2 - Prob. 17E Ch. 1.2 - Prob. 18E Ch. 1.2 - Prob. 19E Ch. 1.2 - Prob. 20E Ch. 1.2 - Prob. 21E Ch. 1.2 - Prob. 22E Ch. 1.2 - Prob. 23E Ch. 1.2 - Prob. 24E Ch. 1.2 - Prob. 25E Ch. 1.2 - Prob. 26E Ch. 1.2 - Prob. 27E Ch. 1.2 - Prob. 28E Ch. 1.2 - Prob. 29E Ch. 1.2 - Prob. 30E Ch. 1.2 - Prob. 31E Ch. 1.2 - Prob. 32E Ch. 1.2 - Prob. 33E Ch. 1.2 - Prob. 34E Ch. 1.2 - Prob. 35E Ch. 1.2 - Prob. 36E Ch. 1.2 - Prob. 37E Ch. 1.2 - Prob. 38E Ch. 1.2 - Prob. 39E Ch. 1.2 - Prob. 40E Ch. 1.2 - Prob. 41E Ch. 1.2 - Prob. 42E Ch. 1.2 - Prob. 43E Ch. 1.2 - Prob. 44E Ch. 1.2 - Prob. 45E Ch. 1.2 - Prob. 46E Ch. 1.2 - Prob. 47E Ch. 1.2 - Prob. 48E Ch. 1.2 - Prob. 49E Ch. 1.2 - Prob. 50E Ch. 1.2 - Prob. 51E Ch. 1.2 - Prob. 52E Ch. 1.2 - Prob. 53E Ch. 1.2 - Prob. 54E Ch. 1.2 - Prob. 55E Ch. 1.2 - Prob. 56E Ch. 1.2 - Prob. 57E Ch. 1.2 - Prob. 58E Ch. 1.2 - Prob. 59E Ch. 1.2 - Prob. 60E Ch. 1.2 - Prob. 61E Ch. 1.2 - Prob. 62E Ch. 1.2 - Prob. 63E Ch. 1.2 - Prob. 64E Ch. 1.2 - Prob. 65E Ch. 1.2 - Prob. 66E Ch. 1.2 - Prob. 67E Ch. 1.2 - Prob. 68E Ch. 1.2 - Prob. 69E Ch. 1.2 - Prob. 70E Ch. 1.2 - Prob. 71E Ch. 1.2 - Prob. 72E Ch. 1.3 - Prob. 1QR Ch. 1.3 - Prob. 2QR Ch. 1.3 - Prob. 3QR Ch. 1.3 - Prob. 4QR Ch. 1.3 - Prob. 5QR Ch. 1.3 - Prob. 6QR Ch. 1.3 - Prob. 7QR Ch. 1.3 - Prob. 8QR Ch. 1.3 - Prob. 9QR Ch. 1.3 - Prob. 10QR Ch. 1.3 - Prob. 1E Ch. 1.3 - Prob. 2E Ch. 1.3 - Prob. 3E Ch. 1.3 - Prob. 4E Ch. 1.3 - Prob. 5E Ch. 1.3 - Prob. 6E Ch. 1.3 - Prob. 7E Ch. 1.3 - Prob. 8E Ch. 1.3 - Prob. 9E Ch. 1.3 - Prob. 10E Ch. 1.3 - Prob. 11E Ch. 1.3 - Prob. 12E Ch. 1.3 - Prob. 13E Ch. 1.3 - Prob. 14E Ch. 1.3 - Prob. 15E Ch. 1.3 - Prob. 16E Ch. 1.3 - Prob. 17E Ch. 1.3 - Prob. 18E Ch. 1.3 - Prob. 19E Ch. 1.3 - Prob. 20E Ch. 1.3 - Prob. 21E Ch. 1.3 - Prob. 22E Ch. 1.3 - Prob. 23E Ch. 1.3 - Prob. 24E Ch. 1.3 - Prob. 25E Ch. 1.3 - Prob. 26E Ch. 1.3 - Prob. 27E Ch. 1.3 - Prob. 28E Ch. 1.3 - Prob. 29E Ch. 1.3 - Prob. 30E Ch. 1.3 - Prob. 31E Ch. 1.3 - Prob. 32E Ch. 1.3 - Prob. 33E Ch. 1.3 - Prob. 34E Ch. 1.3 - Prob. 35E Ch. 1.3 - Prob. 36E Ch. 1.3 - Prob. 37E Ch. 1.3 - Prob. 38E Ch. 1.3 - Prob. 39E Ch. 1.3 - Prob. 40E Ch. 1.3 - Prob. 41E Ch. 1.3 - Prob. 42E Ch. 1.3 - Prob. 43E Ch. 1.3 - Prob. 44E Ch. 1.3 - Prob. 45E Ch. 1.3 - Prob. 46E Ch. 1.3 - Prob. 47E Ch. 1.3 - Prob. 48E Ch. 1.3 - Prob. 49E Ch. 1.3 - Prob. 1QQ Ch. 1.3 - Prob. 2QQ Ch. 1.3 - Prob. 3QQ Ch. 1.3 - Prob. 4QQ Ch. 1.4 - Prob. 1QR Ch. 1.4 - Prob. 2QR Ch. 1.4 - Prob. 3QR Ch. 1.4 - Prob. 4QR Ch. 1.4 - Prob. 5QR Ch. 1.4 - Prob. 6QR Ch. 1.4 - Prob. 7QR Ch. 1.4 - Prob. 8QR Ch. 1.4 - Prob. 9QR Ch. 1.4 - Prob. 10QR Ch. 1.4 - Prob. 1E Ch. 1.4 - Prob. 2E Ch. 1.4 - Prob. 3E Ch. 1.4 - Prob. 4E Ch. 1.4 - Prob. 5E Ch. 1.4 - Prob. 6E Ch. 1.4 - Prob. 7E Ch. 1.4 - Prob. 8E Ch. 1.4 - Prob. 9E Ch. 1.4 - Prob. 10E Ch. 1.4 - Prob. 11E Ch. 1.4 - Prob. 12E Ch. 1.4 - Prob. 13E Ch. 1.4 - Prob. 14E Ch. 1.4 - Prob. 15E Ch. 1.4 - Prob. 16E Ch. 1.4 - Prob. 17E Ch. 1.4 - Prob. 18E Ch. 1.4 - Prob. 19E Ch. 1.4 - Prob. 20E Ch. 1.4 - Prob. 21E Ch. 1.4 - Prob. 22E Ch. 1.4 - Prob. 23E Ch. 1.4 - Prob. 24E Ch. 1.4 - Prob. 25E Ch. 1.4 - Prob. 26E Ch. 1.4 - Prob. 27E Ch. 1.4 - Prob. 28E Ch. 1.4 - Prob. 29E Ch. 1.4 - Prob. 30E Ch. 1.4 - Prob. 31E Ch. 1.4 - Prob. 32E Ch. 1.4 - Prob. 33E Ch. 1.4 - Prob. 34E Ch. 1.4 - Prob. 35E Ch. 1.4 - Prob. 36E Ch. 1.4 - Prob. 37E Ch. 1.4 - Prob. 38E Ch. 1.4 - Prob. 39E Ch. 1.4 - Prob. 40E Ch. 1.4 - Prob. 41E Ch. 1.4 - Prob. 42E Ch. 1.4 - Prob. 43E Ch. 1.4 - Prob. 44E Ch. 1.4 - Prob. 45E Ch. 1.4 - Prob. 46E Ch. 1.4 - Prob. 47E Ch. 1.4 - Prob. 48E Ch. 1.5 - Prob. 1QR Ch. 1.5 - Prob. 2QR Ch. 1.5 - Prob. 3QR Ch. 1.5 - Prob. 4QR Ch. 1.5 - Prob. 5QR Ch. 1.5 - Prob. 6QR Ch. 1.5 - Prob. 7QR Ch. 1.5 - Prob. 8QR Ch. 1.5 - Prob. 9QR Ch. 1.5 - Prob. 10QR Ch. 1.5 - Prob. 1E Ch. 1.5 - Prob. 2E Ch. 1.5 - Prob. 3E Ch. 1.5 - Prob. 4E Ch. 1.5 - Prob. 5E Ch. 1.5 - Prob. 6E Ch. 1.5 - Prob. 7E Ch. 1.5 - Prob. 8E Ch. 1.5 - Prob. 9E Ch. 1.5 - Prob. 10E Ch. 1.5 - Prob. 11E Ch. 1.5 - Prob. 12E Ch. 1.5 - Prob. 13E Ch. 1.5 - Prob. 14E Ch. 1.5 - Prob. 15E Ch. 1.5 - Prob. 16E Ch. 1.5 - Prob. 17E Ch. 1.5 - Prob. 18E Ch. 1.5 - Prob. 19E Ch. 1.5 - Prob. 20E Ch. 1.5 - Prob. 21E Ch. 1.5 - Prob. 22E Ch. 1.5 - Prob. 23E Ch. 1.5 - Prob. 24E Ch. 1.5 - Prob. 25E Ch. 1.5 - Prob. 26E Ch. 1.5 - Prob. 27E Ch. 1.5 - Prob. 28E Ch. 1.5 - Prob. 29E Ch. 1.5 - Prob. 30E Ch. 1.5 - Prob. 31E Ch. 1.5 - Prob. 32E Ch. 1.5 - Prob. 33E Ch. 1.5 - Prob. 34E Ch. 1.5 - Prob. 35E Ch. 1.5 - Prob. 36E Ch. 1.5 - Prob. 37E Ch. 1.5 - Prob. 38E Ch. 1.5 - Prob. 39E Ch. 1.5 - Prob. 40E Ch. 1.5 - Prob. 41E Ch. 1.5 - Prob. 42E Ch. 1.5 - Prob. 43E Ch. 1.5 - Prob. 44E Ch. 1.5 - Prob. 45E Ch. 1.5 - Prob. 46E Ch. 1.5 - Prob. 47E Ch. 1.5 - Prob. 48E Ch. 1.5 - Prob. 49E Ch. 1.5 - Prob. 50E Ch. 1.5 - Prob. 51E Ch. 1.5 - Prob. 52E Ch. 1.5 - Prob. 53E Ch. 1.5 - Prob. 54E Ch. 1.5 - Prob. 55E Ch. 1.5 - Prob. 56E Ch. 1.5 - Prob. 57E Ch. 1.5 - Prob. 58E Ch. 1.5 - Prob. 59E Ch. 1.5 - Prob. 60E Ch. 1.5 - Prob. 61E Ch. 1.5 - Prob. 62E Ch. 1.6 - Prob. 1QR Ch. 1.6 - Prob. 2QR Ch. 1.6 - Prob. 3QR Ch. 1.6 - Prob. 4QR Ch. 1.6 - Prob. 5QR Ch. 1.6 - Prob. 6QR Ch. 1.6 - Prob. 7QR Ch. 1.6 - Prob. 8QR Ch. 1.6 - Prob. 9QR Ch. 1.6 - Prob. 10QR Ch. 1.6 - Prob. 1E Ch. 1.6 - Prob. 2E Ch. 1.6 - Prob. 3E Ch. 1.6 - Prob. 4E Ch. 1.6 - Prob. 5E Ch. 1.6 - Prob. 6E Ch. 1.6 - Prob. 7E Ch. 1.6 - Prob. 8E Ch. 1.6 - Prob. 9E Ch. 1.6 - Prob. 10E Ch. 1.6 - Prob. 11E Ch. 1.6 - Prob. 12E Ch. 1.6 - Prob. 13E Ch. 1.6 - Prob. 14E Ch. 1.6 - Prob. 15E Ch. 1.6 - Prob. 16E Ch. 1.6 - Prob. 17E Ch. 1.6 - Prob. 18E Ch. 1.6 - Prob. 19E Ch. 1.6 - Prob. 20E Ch. 1.6 - Prob. 21E Ch. 1.6 - Prob. 22E Ch. 1.6 - Prob. 23E Ch. 1.6 - Prob. 24E Ch. 1.6 - Prob. 25E Ch. 1.6 - Prob. 26E Ch. 1.6 - Prob. 27E Ch. 1.6 - Prob. 28E Ch. 1.6 - Prob. 29E Ch. 1.6 - Prob. 30E Ch. 1.6 - Prob. 31E Ch. 1.6 - Prob. 32E Ch. 1.6 - Prob. 33E Ch. 1.6 - Prob. 34E Ch. 1.6 - Prob. 35E Ch. 1.6 - Prob. 36E Ch. 1.6 - Prob. 37E Ch. 1.6 - Prob. 38E Ch. 1.6 - Prob. 39E Ch. 1.6 - Prob. 40E Ch. 1.6 - Prob. 41E Ch. 1.6 - Prob. 42E Ch. 1.6 - Prob. 43E Ch. 1.6 - Prob. 44E Ch. 1.6 - Prob. 45E Ch. 1.6 - Prob. 46E Ch. 1.6 - Prob. 47E Ch. 1.6 - Prob. 48E Ch. 1.6 - Prob. 49E Ch. 1.6 - Prob. 50E Ch. 1.6 - Prob. 51E Ch. 1.6 - Prob. 52E Ch. 1.6 - Prob. 53E Ch. 1.6 - Prob. 54E Ch. 1.6 - Prob. 55E Ch. 1.6 - Prob. 56E Ch. 1.6 - Prob. 57E Ch. 1.6 - Prob. 58E Ch. 1.6 - Prob. 59E Ch. 1.6 - Prob. 60E Ch. 1.6 - Prob. 61E Ch. 1.6 - Prob. 62E Ch. 1.6 - Prob. 1QQ Ch. 1.6 - Prob. 2QQ Ch. 1.6 - Prob. 3QQ Ch. 1.6 - Prob. 4QQ Ch. 1 - Prob. 1RE Ch. 1 - Prob. 2RE Ch. 1 - Prob. 3RE Ch. 1 - Prob. 4RE Ch. 1 - Prob. 5RE Ch. 1 - Prob. 6RE Ch. 1 - Prob. 7RE Ch. 1 - Prob. 8RE Ch. 1 - Prob. 9RE Ch. 1 - Prob. 10RE Ch. 1 - Prob. 11RE Ch. 1 - Prob. 12RE Ch. 1 - Prob. 13RE Ch. 1 - Prob. 14RE Ch. 1 - Prob. 15RE Ch. 1 - Prob. 16RE Ch. 1 - Prob. 17RE Ch. 1 - Prob. 18RE Ch. 1 - Prob. 19RE Ch. 1 - Prob. 20RE Ch. 1 - Prob. 21RE Ch. 1 - Prob. 22RE Ch. 1 - Prob. 23RE Ch. 1 - Prob. 24RE Ch. 1 - Prob. 25RE Ch. 1 - Prob. 26RE Ch. 1 - Prob. 27RE Ch. 1 - Prob. 28RE Ch. 1 - Prob. 29RE Ch. 1 - Prob. 30RE Ch. 1 - Prob. 31RE Ch. 1 - Prob. 32RE Ch. 1 - Prob. 33RE Ch. 1 - Prob. 34RE Ch. 1 - Prob. 35RE Ch. 1 - Prob. 36RE Ch. 1 - Prob. 37RE Ch. 1 - Prob. 38RE Ch. 1 - Prob. 39RE Ch. 1 - Prob. 40RE Ch. 1 - Prob. 41RE Ch. 1 - Prob. 42RE Ch. 1 - Prob. 43RE Ch. 1 - Prob. 44RE Ch. 1 - Prob. 45RE Ch. 1 - Prob. 46RE Ch. 1 - Prob. 47RE Ch. 1 - Prob. 48RE Ch. 1 - Prob. 49RE Ch. 1 - Prob. 50RE Ch. 1 - Prob. 51RE Ch. 1 - Prob. 52RE Ch. 1 - Prob. 53RE Ch. 1 - Prob. 54RE Ch. 1 - Prob. 55RE Ch. 1 - Prob. 56RE Ch. 1 - Prob. 57RE Ch. 1 - Prob. 58RE Ch. 1 - Prob. 59RE Ch. 1 - Prob. 60RE Ch. 1 - Prob. 61RE Ch. 1 - Prob. 62RE Ch. 1 - Prob. 63RE Ch. 1 - Prob. 64RE Ch. 1 - Prob. 65RE Ch. 1 - Prob. 66RE Ch. 1 - Prob. 67RE Ch. 1 - Prob. 68RE Ch. 1 - Prob. 69RE Ch. 1 - Prob. 70RE

Additional Math Textbook Solutions

Find more solutions based on key concepts

In a right triangle, with legs a and b and hypotenuse c , the Pythagorean Theorem states that _______. (p. A14)

Precalculus

In Exercises 29–32, indicate whether the observational study used is cross-sectional, retrospective, or prospec...

Elementary Statistics (13th Edition)

3. Voluntary Response Sample What is a voluntary response sample, and why is such a sample generally not suitab...

Elementary Statistics

Snow Depth (Example 3) Eric wants to go skiing tomorrow, but only if there are 3 inches or more of new snow. Ac...

Introductory Statistics

Write a sentence that illustrates the use of 78 in each of the following ways. a. As a division problem. b. As ...

A Problem Solving Approach To Mathematics For Elementary School Teachers (13th Edition)

Hypothesis Testing Using a P-Value In Exercises 31–36, identify the claim and state H0 and Ha. find the standar...

Elementary Statistics: Picturing the World (7th Edition)

Knowledge Booster

$Calculus$

Learn more about

Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, calculus and related others by exploring similar questions and additional content below.