
Concept explainers
(a)
To draw: Thecomplete graph of the a function if it is even by the help of given portion of the graph in the interval
(a)
Explanation of Solution
Given information:A portion of the graph of a function as shown below:
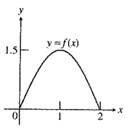
Figure (1)
The function is an even function.
Graph:
Consider that the function for the given graph is an even function.
It is known that the graph of an even function is symmetric about the y -axis. For even function, if a point
From the given graph it can be observed that a portion of the graph is drawn in the interval
Draw the symmetric graph in the interval

Figure (2)
Interpretation: From the graph it can be observed that if point
(b)
To draw: The complete graph of the a function if it is odd by the help of given portion of the graph in the interval
(b)
Explanation of Solution
Given information:A portion of the graph of a function as shown below:
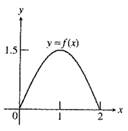
Figure (1)
The function is an odd function.
Graph:
Consider that the function for the given graph is an odd function.
It is known that the graph of an even function is symmetric about origin. For odd function, if a point
From the given graph it can be observed that a portion of the graph is drawn in the interval
Draw the symmetric graph about the origin in the interval

Figure (2)
Interpretation: From the graph it can be observed that if point
Chapter 1 Solutions
Calculus 2012 Student Edition (by Finney/Demana/Waits/Kennedy)
Additional Math Textbook Solutions
Elementary Statistics (13th Edition)
Introductory Statistics
Elementary Statistics
Elementary Statistics: Picturing the World (7th Edition)
Calculus: Early Transcendentals (2nd Edition)
- 39. (a) Show that Σeak converges for each α > 0. (b) Show that keak converges for each a > 0. k=0 (c) Show that, more generally, Σk"eak converges for each k=0 nonnegative integer n and each a > 0.arrow_forward#3 Find the derivative y' = of the following functions, using the derivative rules: dx a) y-Cos 6x b) y=x-Sin4x c) y=x-Cos3x d) y=x-R CD-X:-:TCH :D:D:D - Sin f) Sin(x²) (9) Tan (x³)arrow_forwardmate hat is the largest area that can be en 18 For the function y=x³-3x² - 1, use derivatives to: (a) determine the intervals of increase and decrease. (b) determine the local (relative) maxima and minima. (c) determine the intervals of concavity. (d) determine the points of inflection. b) (e) sketch the graph with the above information indicated on the graph.arrow_forward
- use L'Hopital Rule to evaluate the following. a) 4x3 +10x2 23009׳-9 943-9 b) hm 3-84 хто бу+2 < xan x-30650)arrow_forwardEvaluate the next integralarrow_forward1. For each of the following, find the critical numbers of f, the intervals on which f is increasing or decreasing, and the relative maximum and minimum values of f. (a) f(x) = x² - 2x²+3 (b) f(x) = (x+1)5-5x-2 (c) f(x) = x2 x-9 2. For each of the following, find the intervals on which f is concave upward or downward and the inflection points of f. (a) f(x) = x - 2x²+3 (b) g(x) = x³- x (c) f(x)=x-6x3 + x-8 3. Find the relative maximum and minimum values of the following functions by using the Second Derivative Test. (a) f(x)=1+3x² - 2x3 (b) g(x) = 2x3 + 3x² - 12x-4arrow_forward
 Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning
Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON
Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
 Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning
Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning





