
(a)
To find: The graph of the parametric equations, initial and terminal points. Also, indicate the direction in which the curve is traced.
(a)
Answer to Problem 14E
The graph of the parametric equations is shown in figure (1), the initial point and terminal point is
Explanation of Solution
Given information: The equations are
Calculation:
Use the following step to graph the parametric equations by graphing calculator.
Step 1: First press the “ON” button graphical calculator.
Step 2: Press the
Step 3: Press
Step 4: Press
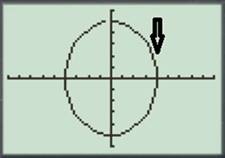
Figure (1)
If
If
Therefore, the graph of the parametric equations is shown in figure (1), the initial point and terminal point is
(b)
To find: The Cartesian equation for a curve that contains the parameterized curve and the portion of the graph of the Cartesian equation that is traced by the parameterized curve.
(b)
Answer to Problem 14E
The Cartesian equation for a curve that contains the parameterized curve is
Explanation of Solution
Given information: The equations are
Calculation:
Rewrite the parametric equations as
Add the equations
As shown in the graph, the parameterized curve traces all of the ellipse defined by
Therefore, the Cartesian equation for a curve that contains the parameterized curve is
Chapter 1 Solutions
Calculus 2012 Student Edition (by Finney/Demana/Waits/Kennedy)
Additional Math Textbook Solutions
Calculus: Early Transcendentals (2nd Edition)
A First Course in Probability (10th Edition)
Introductory Statistics
Algebra and Trigonometry (6th Edition)
Pre-Algebra Student Edition
- Let the region R be the area enclosed by the function f(x)= = 3x² and g(x) = 4x. If the region R is the base of a solid such that each cross section perpendicular to the x-axis is an isosceles right triangle with a leg in the region R, find the volume of the solid. You may use a calculator and round to the nearest thousandth. y 11 10 9 00 8 7 9 5 4 3 2 1 -1 -1 x 1 2arrow_forwardLet the region R be the area enclosed by the function f(x) = ex — 1, the horizontal line y = -4 and the vertical lines x = 0 and x = 3. Find the volume of the solid generated when the region R is revolved about the line y = -4. You may use a calculator and round to the nearest thousandth. 20 15 10 5 y I I I | I + -1.5 -1 -0.5 0.5 1 1.5 2 2.5 3 -5 I -10 -15 I + I I T I I + -20 I + -25 I I I -30 I 3.5 4 xarrow_forwardplease show all the workarrow_forward
 Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning
Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON
Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
 Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning
Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning





