Operations and Supply Chain Management, 9th Edition WileyPLUS Registration Card + Loose-leaf Print Companion
9th Edition
ISBN: 9781119371618
Author: Roberta S. Russell
Publisher: Wiley (WileyPLUS Products)
expand_more
expand_more
format_list_bulleted
Concept explainers
Question
Chapter 14.S, Problem 17P
a)
Summary Introduction
To determine: the quantity of each product to produce in order to maximum profit by formulating linear programming and solves it graphically.
Introduction: Linear programming is used to obtain the best possible outcome from the given real-world problem which is subjective to constraints and inequalities. It is used to make decisions based on business objectives. It is used in business planning, industrial engineering, and physical science. Express the real-world problem into the mathematical expression to get the optimal solution from the linear programming.
b)
Summary Introduction
To determine: slope of each objective function and change the objective function to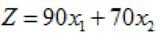 
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
Read the project statement and answer ALL of the questions that follow
PROJECT STATEMENT
The African Integrated High-Speed Railway Network (AIHSRN).
African nations are preparing to invest billions in a significant overhaul of their rail infrastructure as part of an ambitious plan
for the continent. One of the key projects underway is the African Integrated High-Speed Railway Network (AIHSRN), which
aims to connect Africa's capital cities and major commercial centres with a high-speed railway network to enhance
continental trade and competition. This network will span 2,000 km (1,243 miles) and connect 60 cities, including Nairobi,
Lagos, Cairo, and Dakar. It will improve access to essential markets, enhance economic cooperation, and encourage
regional collaboration. The plan is poised to revolutionise intra-African trade by reducing travel times and lowering
transportation costs, making trade between African nations more competitive. The trains will be capable of reaching speeds
of up…
In the Sally Soprano case, Sally's agent prepares the potential issues to be discussed before the negotiation. Which items) may be on the list?
Sally's salary and publicity
Work-related benefits and incentives such as a hotel suite accommodation, limousine transportation, flower arrangements in the dressing room
Future contracts and collaboration
Rehearsal setup and arrangements
All of the choices
Summarize chapters 1 through 8 of the book "food and beverage cost control"
Chapter 14 Solutions
Operations and Supply Chain Management, 9th Edition WileyPLUS Registration Card + Loose-leaf Print Companion
Ch. 14.S - Prob. 1QCh. 14.S - Prob. 2QCh. 14.S - Prob. 3QCh. 14.S - Prob. 4QCh. 14.S - Prob. 5QCh. 14.S - Prob. 6QCh. 14.S - Prob. 7QCh. 14.S - Prob. 8QCh. 14.S - Prob. 1PCh. 14.S - The Tycron Company produces three electrical...
Ch. 14.S - Prob. 3PCh. 14.S - The Pinewood Cabinet and Furniture Company...Ch. 14.S - The Mystic Coffee Shop blends coffee on the...Ch. 14.S - Prob. 6PCh. 14.S - Prob. 7PCh. 14.S - Prob. 8PCh. 14.S - Prob. 9PCh. 14.S - Prob. 10PCh. 14.S - Prob. 11PCh. 14.S - Prob. 12PCh. 14.S - Prob. 13PCh. 14.S - Prob. 14PCh. 14.S - Prob. 15PCh. 14.S - Prob. 16PCh. 14.S - Prob. 17PCh. 14.S - Prob. 18PCh. 14.S - Prob. 19PCh. 14.S - Prob. 20PCh. 14.S - Prob. 22PCh. 14.S - Prob. 23PCh. 14.S - Prob. 24PCh. 14.S - Prob. 25PCh. 14.S - Prob. 27PCh. 14.S - Prob. 28PCh. 14.S - Prob. 1.1CPCh. 14.S - Prob. 1.2CPCh. 14.S - Prob. 1.3CPCh. 14.S - Prob. 1.4CPCh. 14.S - Prob. 1.5CPCh. 14.S - Prob. 1.6CPCh. 14.S - Prob. 1.7CPCh. 14.S - Prob. 1.8CPCh. 14.S - Prob. 1.9CPCh. 14.S - Prob. 2.1CPCh. 14 - Prob. 1.1ASCCh. 14 - Prob. 1.2ASCCh. 14 - Supply and Demand in the Spirits Industry A...Ch. 14 - Supply and Demand in the Spirits Industry A...Ch. 14 - Supply and Demand in the Spirits Industry A...Ch. 14 - Disneys Magic Numbers Sales and operations...Ch. 14 - Disneys Magic Numbers Sales and operations...Ch. 14 - Prob. 1QCh. 14 - List several alternatives for adjusting capacity....Ch. 14 - Prob. 3QCh. 14 - How do linear programming, the linear decision...Ch. 14 - Prob. 5QCh. 14 - What options are available for altering the...Ch. 14 - Prob. 7QCh. 14 - Prob. 8QCh. 14 - Explain the process of collaborative planning. How...Ch. 14 - Prob. 11QCh. 14 - Prob. 12QCh. 14 - Prob. 1PCh. 14 - Prob. 2PCh. 14 - Prob. 3PCh. 14 - Prob. 4PCh. 14 - Mamas Stuffin is a popular food item during the...Ch. 14 - Prob. 6PCh. 14 - Slopes Sleds (SS) makes skis, snowboards, and...Ch. 14 - Prob. 8PCh. 14 - Midlife Shoes, Inc, is a manufacturer of sensible...Ch. 14 - Design a production plan for Mamas Stuffin in...Ch. 14 - Design a production plan for FansForYou in Problem...Ch. 14 - Prob. 16PCh. 14 - Prob. 17PCh. 14 - Prob. 18PCh. 14 - Prob. 19PCh. 14 - Prob. 20PCh. 14 - Prob. 21PCh. 14 - Prob. 22PCh. 14 - How many units are available-to-promise in period...Ch. 14 - Complete the available-to-promise table below.Ch. 14 - Complete the available-to-promise table below.Ch. 14 - Calculate the available-to-promise row in the...Ch. 14 - Complete the following table. How many Bs are...Ch. 14 - Managers at the Dew Drop Inn are concerned about...Ch. 14 - Prob. 29PCh. 14 - Prob. 30PCh. 14 - Prob. 31PCh. 14 - Prob. 32PCh. 14 - The Forestry Club sells Christmas trees each year...Ch. 14 - Prob. 34PCh. 14 - Tariott Hotel rents rooms for 125 a night that...Ch. 14 - Prob. 36PCh. 14 - Prob. 1.1CPCh. 14 - Prob. 1.2CPCh. 14 - Prob. 1.3CP
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, operations-management and related others by exploring similar questions and additional content below.Similar questions
- Can you guys help me with this? Thank you! Here's the question: Compared to the CONSTRAINT model, how has the network changed? How do you plan to add contingency to your network? Please answer this thoroughly Here's the what-if scenario: Assume that the LA warehouse becomes temporarily or even indefinitely disabled since facing a large-scale labor disruption. Re-optimize the network considering this new constraint. Here's the scenario comparison analysis: Scenario Constraint Scenario vs What-if Scenario Summary The Constraint Scenario exhibits a higher total cost of $7,424,575.45 compared to the What-if Scenario's total cost of $6,611,905.60, signifying a difference of approximately $812,669.85, which indicates a more expensive operation in the Constraint Scenario. The average service time is slightly higher in the Constraint Scenario (0.72 days vs. 0.70 days), suggesting that the What-if Scenario provides a marginally quicker service. Moreover, the average end-to-end service time…arrow_forwardCan you guys help me with this? Thank you! Here's the question: Compared to the CONSTRAINT model, how has the network changed? How do you plan to add contingency to your network? Please answer this throughly Here's the what-if scenario: Assume that Dallas plant has lost power. It cannot serve the DCs anymore and has to remain locked indefinitely. Re-optimize the network considering this new constraint. Here's the scenario comparison analysis: Scenario Constraint Scenario vs What-if Scenario Summary In comparing the Constraint Scenario to the What-if Scenario, a few key differences highlight the efficiencies evident in the supply chain. Firstly, the total cost in the Constraint Scenario is lower at $7,424,575.45, while the What-if Scenario incurs a total cost of $7,486,369.12, resulting in a cost delta of $61,793.67. Additionally, although both scenarios exhibit the same average service time of 0.72 days, the What-if Scenario has a more favorable average end-to-end service time of 2.41…arrow_forwardEmployee In-Service Training ASSIGNMENT: In-Service Training. The intern is required to plan and implement two in-service training sessions for employees. Each in-service should last at least 10 but not more than 30 minutes and should be given to all employees affected. The preceptor or supervisor/unit manager must approve all in-service topics. 1) One presentation should be related to a policy or procedure of any kind (e.g. proper use of equipment); 2) The second presentation must be related to sanitation or safety. For each in-service presentation, the intern must develop a written class plan and a visual aid (may be a handout, poster, PowerPoint slide presentation, etc.) appropriate to the life experiences, cultural diversity and educational background of the target audience. The intern must also measure behavior change. Note, this cannot be measured by a written pre- and post- test. That would be measuring knowledge. The intern mustactually observe and document that the learners…arrow_forward
- A small furniture manufacturer produces tables and chairs. Each product must go through three stages of the manufacturing process – assembly, finishing, and inspection. Each table requires 3 hours of assembly, 2 hours of finishing, and 1 hour of inspection. The profit per table is $120 while the profit per chair is $80. Currently, each week there are 200 hours of assembly time available, 180 hours of finishing time, and 40 hours of inspection time. Linear programming is to be used to develop a production schedule. Define the variables as follows: T = number of tables produced each week C= number of chairs produced each week According to the above information, what would the objective function be? (a) Maximize T+C (b) Maximize 120T + 80C (c) Maximize 200T+200C (d) Minimize 6T+5C (e) none of the above According to the information provided in Question 17, which of the following would be a necessary constraint in the problem? (a) T+C ≤ 40 (b) T+C ≤ 200 (c) T+C ≤ 180 (d) 120T+80C ≥ 1000…arrow_forwardAs much detail as possible. Dietary Management- Nursing Home Don't add any fill-in-the-blanksarrow_forwardMenu Planning Instructions Use the following questions and points as a guide to completing this assignment. The report should be typed. Give a copy to the facility preceptor. Submit a copy in your Foodservice System Management weekly submission. 1. Are there any federal regulations and state statutes or rules with which they must comply? Ask preceptor about regulations that could prescribe a certain amount of food that must be kept on hand for emergencies, etc. Is the facility accredited by any agency such as Joint Commission? 2. Describe the kind of menu the facility uses (may include standard select menu, menu specific to station, non-select, select, room service, etc.) 3. What type of foodservice does the facility have? This could be various stations to choose from, self-serve, 4. conventional, cook-chill, assembly-serve, etc. Are there things about the facility or system that place a constraint on the menu to be served? Consider how patients/guests are served (e.g. do they serve…arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Practical Management ScienceOperations ManagementISBN:9781337406659Author:WINSTON, Wayne L.Publisher:Cengage,
Practical Management Science
Operations Management
ISBN:9781337406659
Author:WINSTON, Wayne L.
Publisher:Cengage,