Chapter 13.8, Problem 42PPS

a.

To determine

Explain the amplitude, period, and the midline of the function that approximate the temperature y on day d.

Answer to Problem 42PPS

The amplitude, period and the midline are $45,5\&4$ .

Explanation of Solution

Given: It is given in the question that in one month, the outside temperature fluctuates between ${40}^{\circ }F$ and ${50}^{\circ }F$ . A cosine curve approximates the change in temperature, with a high of ${50}^{\circ }F$ being reached every four days.

Concept Used:

In this, use the concept of general equation of cosine $y=a\cos d(t)+h$ , where a is the amplitude, $\frac{2\pi }{\left|b\right|}$ is the period and h is the midline and it is the average between the maximum and minimum value, d is the day.

Calculation: Since, the maximum and minimum are ${50}^{\circ }F\&{40}^{\circ }F$ .

First find the midline d,

  $\begin{array}{l}\frac{50+40}{2}=\frac{90}{2}=45\\ h=45\end{array}$

Since, the amplitude is the difference between midline and maximum and minimum value.

  $\begin{array}{l}50-45=5\\ a=5\end{array}$

It takes four days from the maximum to minimum which is its period.

So, the period is $4$ .

Conclusion:

The amplitude, period and the midline are $45,5\&4$ .

b.

To determine

Find the cosine function to estimate the temperature y on day d.

Answer to Problem 42PPS

The function is $y=5\cos (\frac{\pi }{2}d)+45$ .

Explanation of Solution

Given: It is given in the question that he amplitude, period and the midline are $45,5\&4$ .

Concept Used:

In this, use the concept of general equation of cosine $y=a\cos b(d)+h$ , where a is the amplitude, $\frac{2\pi }{\left|b\right|}$ is the period and h is the midline and it is the average between the maximum and minimum value, d is the day.

Calculation: Let the equation be $y=a\cos b(d)+h$ .

Since,

  $\begin{array}{l}\frac{2\pi }{\left|b\right|}=4\\ b=\frac{2\pi }{4}\\ b=\frac{\pi }{2}\end{array}$

Now,

  $\begin{array}{l}a=5\\ b=\frac{\pi }{2}\\ h=45\\ period=4\end{array}$

Put the above value in the equation $y=a\cos b(d)+h$

The equation is $y=5\cos (\frac{\pi }{2}d)+45$ .

Conclusion:

The function is $y=5\cos (\frac{\pi }{2}d)+45$ .

c.

To determine

Draw the graph of the function.

Explanation of Solution

Given:

It is given in the question that the function is $y=5\cos (\frac{\pi }{2}d)+45$ .

Graph:

  

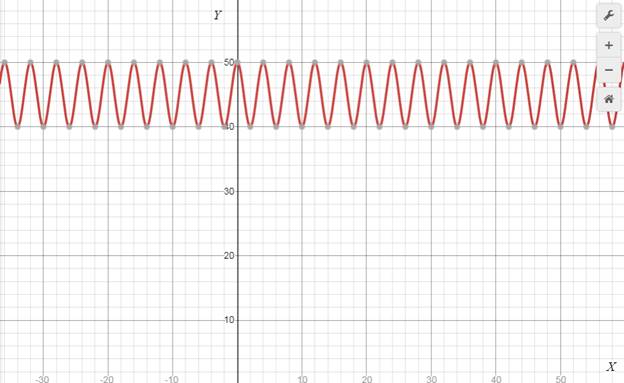
Interpretation:

Here, put the function $y=5\cos (\frac{\pi }{2}d)+45$ in the graphing calculator, it gives the required graph in the right way. It gives cosine curve.

d.

To determine

Calculate the temperature of the seventh day of the month.

Answer to Problem 42PPS

The temperature will be ${45}^{\circ }$ .

Explanation of Solution

Given:

It is given in the question that the function is $y=5\cos (\frac{\pi }{2}d)+45$ .

Concept Used:

In this, use the concept of substituting the given value in the function and get the solution.

Calculation: Here, the function $y=5\cos (\frac{\pi }{2}d)+45$ .

Substitute the value $d=7$ in the above function,

  $\begin{array}{l}y=5\cos (\frac{\pi }{2}d)+45\\ y=5\cos (\frac{\pi }{2}\cdot 7)+45\\ y=5\cos (\frac{7\pi }{2})+45\\ y=5\cdot 0+45(\cos \frac{n\pi }{2}=0)\\ y=0+45\\ y=45\end{array}$

Conclusion:

The temperature will be ${45}^{\circ }$ .