Chapter 13.8, Problem 35PPS

To determine

Find the minimum and maximum distances of the buoy from the bottom of the lake when a boat passes by.

Answer to Problem 35PPS

The minimum and maximum distance of the buoy is $10.2ft\&13.8ft$ .

Explanation of Solution

Given: It is given in the question that a buoy marking the swimming area in a lake oscillates each time a speed boat goes by its distance d in feet and t is the time in seconds are given by the function $d=1.8\sin \frac{3\pi }{4}t+12$

Concept Used:

In this, use the concept of the general equation for sine $y=a\sin b\theta +d$ , where a is amplitude, $\frac{2\pi }{\left|b\right|}$ is period and d is the vertical shift and the maximum and minimum value of sine is $1\&-1$ .

Calculation: The graph of the function $d=1.8\sin \frac{3\pi }{4}t+12$ is:

  

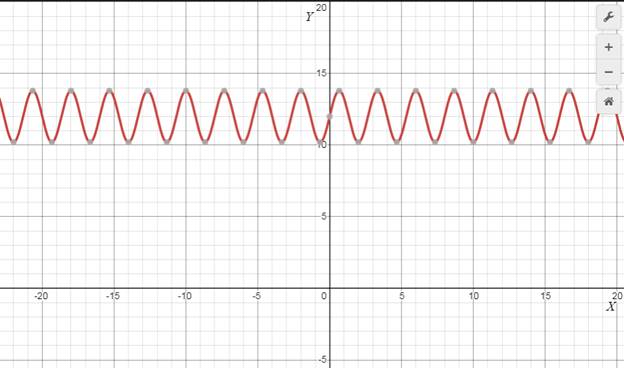
Since, it is know that the minimum value of the sine function is $-1$ :substitute $-1$ for $\sin \frac{3\pi }{4}t$ to get the minimum distance of the buoy from the bottom of the lake:

  $\begin{array}{l}{d}_{\min }=1.8\cdot (-1)+12\\ d_{\min }=-1.8+12\\ d_{\min }=10.2\end{array}$

Now, the maximum value of the sine function is $1$ : Substitute $1$ for $\sin \frac{3\pi }{4}t$ find the maximum distance of the buoy from the bottom of the lake:

  $\begin{array}{l}{d}_{\max }=1.8\cdot (1)+12\\ d_{\max }=1.8+12\\ d_{\max }=13.8\end{array}$

Conclusion:

The minimum and maximum value is

  $10.2ft\&13.8ft$ .